확률 변수
- 통계 조사나 실험 데이터로 도출된 개별 자료를 실수와 대응 시키는 자료
확률 분포
- 확률 변수의 전체적인 분포를 나타내는 개념
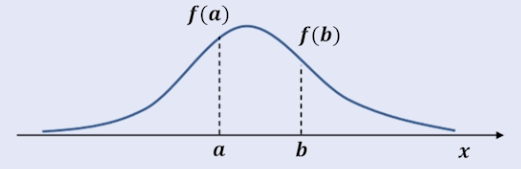
정규 분포 곡선
- 종모양의 확률 밀도 함수
- 평균 근처에 가장 많은 자료 위치
- 양 극단에 위치하는 자료가 줄어듬
확률 변수
1. 확률 변수의 정의
2. 이산 확률 분포
3. 연속 확률 분포
확률 변수 Random Variable
- 어떤 시행에서 일어날 수 있는 모든 경우의 집합 S (표본 공간)의 각 원소를 실수 집합 R의 한 원소에 대응 시키는 함수
- X : S -> R
- 확률 변수는 보통 문자 X, Y, Z 등으로 표기
확률 변수 예시
- 한 개의 동전을 2번 던지는 시행에서 앞면이 나오는 횟수를 X라고 한다면
- S = {(앞, 앞), (앞, 뒤), (뒤, 앞), (뒤, 뒤)}
- X : S -> R
(앞, 앞) -> 2
(앞, 뒤) -> 1
(뒤, 앞) -> 1
(뒤, 뒤) -> 0
확률 변수
- 이산 확률 변수
- 연속 확률 변수
이산 확률 변수
- 치역이 이산 집합인 확률 변수
- ex.1 : 10갸의 동전을 동시에 던질때 앞면이 나온 동전의 개수를 나타내는 확률 변수
- ex.2 : 주사위를 던져서 1의 눈이 나올 때까지 던진 횟수를 나타내는 확률 변수
연속 확률 변수
- 치역이 연속 집합인 확률 변수
- ex.1 : 10cm 씩 커지는 동심워 10개로 구성된 양궁판에 양궁 선수가 활을 쐇을 때, 화살이 꽂힌 위치와 중심으로부터 거리를 나타내는 확률 변수
- ex 2 : 버스 정류장에서 배차 간격이 10분인 버스를 기다리는 시간을 나타내는 확률 변수
이산 확률 분포의 확률 질량 함수
- 이산 확률 변수 X에 대해 임의의 실수 x를 취할 확률을 대응 시키는 함수
- f(x) = Pr(X = x)로 표기
이산 확률 분포의 확률 질량 함수의 예시
- 한 개의 동전을 2번 던지는 시행에서 앞면이 나오는 횟수를 x라 한다면
- S = {(앞, 앞), (앞, 뒤), (뒤, 앞), (뒤, 뒤)}
- X : S -> R
(앞, 앞) -> 2
(앞, 뒤) -> 1
(뒤, 앞) -> 1
(뒤, 뒤) -> 0

이산 확률 분포 확률 질량 함수의 성질
- 이산 확률 변서 X의 확률 질량 함수 f(x)에 대해서

- 위의 한개의 동전을 2번 던지는 시행 예시를 참고하면 f(0) + f(1) + f(2) = 1
이산 확률 분포
- 이산 확률 변수 X가 가지는 값과 그 값에서의 확률 질량 함수의 값의 대응 환계 또는 그 대응관계를 나타내는 표
- ex. 한 개의 동전을 2번 던지는 시행에서 앞면이 나오는 횟수를 X라고 한다면

연속확률 분포의 확률 밀도 함수
- 연속 확률 변수 X에 대하여 다음을 만족시키는 함수 f를 X의 확률 밀도 함수라고함
- f(x) >= 0

연속 확률 분포
- 연속 확률 변수 X가 가지는 값과 그 값에서 확률 밀도함수의 값의 대응 관계
- ex. 정규 분포: 확률 변수 X의 확률 밀도 함수가 다음과 같은 확률 분포

이산 확률 변수와 이항 분포
1. 이산 확률 변수의 기댓값
2. 이산 확률 변수의 분산과 표준 편차
3. 이한 분포
이산 확률변수의 기댓값
- 이산 확률변수 x의 기댓값 E(X)는 E(X) = $\sum_x$ x f(x)로 정의됨
- ex. 한 개의 동전을 2번 던지는 시행에서 앞면이 나오는 횟수를 X라고 한다면
- X의 확률 분포

- E(X) = 0 x $\frac{1} {4}$ + 1 x $\frac{1} {2}$ + 2 x $\frac{1} {4}$=1
이산 확률 변수의 기댓값
- 기댓값 성질 : 이산 확률 변수 X와 실수 c에 대하여
- E(c) = c
- E(c X) = c E(X)
- E(X + c) = E(X) + c
이산 확률 변수의 분산
- 이산 확률변수 X와 그 기댓값 $\mu$ = E(X)에 대해 X의 분산 V(X)는 다음과 같이 정의
=> V(X) = $\sum_x$ (x - $\mu$ $)^2$ f(x)
- V(X) = E(( X - $\mu$ $)^2$)
이산 확률 변수의 표준 편차
- 이산 확률 변수 X에 대하여 X의 표준편차 $\sigma$(X)는 다음과 같이 정의함
=> $\sigma$(X) = $\sqrt{V(X)}$
- ex. 한 개의 동전을 2번 던지는 시행에서 앞면이 나오는 횟수를 X라 한다면

분산과 표준 편차의 성질
- 확률 변수 X와 실수 c에 대하여

이산 확률 변수 X의 확률 분포가 다음과 같을 때

- E(X) = 3
- E($X^2$) = 1 x 0.1 + 4 x 0.2 + 9 x 0.3 + 16 x 0.4 = 10
- V(X) = E($X^2$) - E(X$)^2$ = 1
- $\sigma$(X) = 1
베르누이 분포
- 시행 결과가 1(성공) 또는 0(실패) 두 가지 경우만 일어나고 성공 확률이 p인 분포를 베르누이 부포라 하고, B(1, p)로 표기

- 확률 분포 X가 베르누이 분포 B(1, p)를 따르면
-> E(X) = 0 x (1 - p) + 1 x p = p
-> E($X^2$) = $0^2$ x ( 1 - p ) + $1^2$ x p = p
-> V(X) = E($X^2)$ - E(X$)^2$ = p - $p^2$ = p ( 1 - p )
베르누이 분포의 예시
- 주사위를 한번 던지는 시행에서 1의 눈이 나오면 1의 값을, 그 외 눈이 나오면 0의 값을 갖는 확률 변수 X에 대하여
- X는 베르누이 분포 B(1, $\frac{1} {6}$을 따름
- E(X) = p = $\frac{1} {6}$
- V(X) = p(1-p) = $\frac{5} {36}$
이항 분포
- 성공률이 p인 베르누이 시행을 n회 반복한 후 성공 횟수를 X라 할때, X의 확률 분포를 이항분포라 하며 B(n,p)라고 표
기
- 확률 변수 X가 이항 분포 B(n, p)를 따르면
-> f(x) = $\binom{n}{x}$ $p^x$(1 - p$)^{n - x}$, x = 0, 1, ..., n
-> E(X) = np
-> V(X) = np(1-p)
이항 분포의 예시
- 흰 공이 6개, 검은 공이 4개가 들어 있는 주머니에서 임의로 공을 한 개 꺼내어 색을 확인한 후, 다시 넣기를 100번 반복할 때, 흰 공이 나오는 횟수를 확률 변수 X라고 하면, 확률 분포 X가 이항 분포 B(n, p)를 따르면
- X는 이항 분포 B(100, 6/10)을 따름
- E(X) = np = 100 x $\frac{6} {10}$ = 60
- V(X) = np(1-p) = 100 x $\frac{6} {10}$ x $\frac{4} {10}$ = 24
연속확률변수와 정규분포
1. 연속확률변수
2. 정규분포
3. 이항분포와 정규 분포의 관계
확률 밀도 함수
- 연속 확률 변수 X에 대해 다음을 만족시키는 함수 f를 X의 확률밀도함수라고 함
- f(x) >= 0


- 연속 확률 변수 X와 그 확률 밀도 함수 f(x)에 대해 X의 기댓값 E(X)는 다음과 같이 정의됨

- 기댓값의 성질 : 연속 확률 변수 X와 실수 c에 대해
-> E(c) = c
-> E(cX) = cE(X)
- 연속 확률 변수 X와 그 기댓값 $\mu$ = E(X)에 대해 X의 분산 V(X)는 다음과 같이 정의됨

- V(X) = E((X - $\mu$$)^2$)
- $\sigma$(X) = $\sqrt{(X)}$를 X의 표준 편차라 함
분산과 표준 편차의 성질
- 연속확률변수 X와 실수 c에 대하여

정규 분포
- 확률변수 X의 확률밀도함수가 다음과 같이 주어졌을 때
- X는 정규분포를 따른다고 하며 N($\mu$, $\sigma^2$)로 표기


- 확률 변수 X가 정규 분포 N($\mu$, $\sigma^2$)
-> E(X) = $\mu$
-> V(X) = $\sigma^2$
표준 정규분포
- N(0, 1)을 표준 정규분포라 함
 표준 정규분포의 확률밀도함수
표준 정규분포의 확률밀도함수
표준 정규분포표
- Z가 표준정규분포를 따르면
- Pr(Z <= 2) = ?
- Pz(-1 <= Z <= 1.96) = ?
 표준정규분포표
표준정규분포표
정규분포와 표준 정규분포
- 확률변수 X가 정규분포 N($\mu$, $\sigma^2$를 따르면 Z = $\frac{X - \mu} {\sigma}$는 표준 정규 분포를 따름

표준 정규 분포 예시
- X가 정규 분포 N(1, $2^2$)를 따를 떄 -> 표준 정규 분포로 변환 후 계산
Z = $\frac{X - 1} {2}$
2Z = X - 1
2Z + 1 = X
- Pr(X <= 5) = Pr(Z <= 2) = 0. 5 + 0.4972 = 0.9772
이항 분포와 정규 분포의 관계
- 확률 변수 X가 이항 분포 B(n,p)를 따르고 n이 충분히 크면 X는 근사적으로 N(np, np(1-p))를 따름