연결선에 가중치가 부여된 가중 그래프
- 이동하는데 걸리는 시간
- 어느 경로를 선택해야 목적지에 빠르게 도착할까?
-> 최단 경로 문제

네비게이션 시스템은 복잡한 지도와 그래프를 사용.
다익스트라 알고리즘
- 최단 경로 문제를 해결할 수 있는 알고리즘
특수 그래프
1. 오일러 그래프
2. 해밀턴 그래프
오일러 그래프
- 오일러 경로 : 그래프의 모든 연결선을 한번씩만 지나는 경로
- 오일러 순환 : 시작노드와 끝노드가 같은 오일러
- 오일러 그래프 : 오일러 순환을 가지는 그래프

오일러 그래프에 대한 정의
- 연결 그래프의 모든 노드들이 짝수 노드이면 오일러 그래프
-> 노드의 차수 : 노드에 근접하는 연결선 개수
-> 짝수 노드 : 차수가 짝수인 노드
- 연결 그래프의 노드 중 홀수 노드의 개수가 0 또는 2이면 오일러 경로를 가짐

오일러 그래프와 한붓그리기
- 한붓 그리기 : 그래프에서 연필을 떼지 않고 모든 변을 오직 한 번만 지나는 것
- 한붓 그리기가 가능하려면 연결 그래프의 홀수 노드의 개수가 0 또는 2여야 함

쾨니히스베르크 다리 문제
- 오일러는 쾨니히스베르크 다리 문제를 (다중 그래프에서의) 오일러 순환의 존재 여부 문제로 변환하여 해결함
- 오일러 순환이 존재하지 않음 -> 쾨니히스베르크 다리들을 모두 한번씩만 건너서 출발한 곳으로 다시 돌아올 수 없음

해밀턴 그래프
- 해밀턴 경로 : 시작 노드와 끝 노드 빼고 모든 노드를 한번씩만 지나는 경로
- 해밀턴 순환 : 시작노드와 끝노드가 같은 해밀턴 경로
- 해밀턴 그래프 : 해밀턴 순환을 가지는 그래프

NP-complete
- 어떤 그래프에 해밀턴 경로가 존재하는지 여부를 결정하는 문제를 NP-complete 문제라 함.
- 어떤 그래프가 해밀턴 그래프인지 여부를 구하는 문제
윌리엄 로언 해밀턴
- 아일랜드 수학자, 물리학자, 천문학자
- 사원수를 발견할 인물
- 광학, 동역학 및 대수학의 발전에 큰 공헌을 함

순회 판매원 문제
- 방문할 도시들과 이들 도시 사이의 거리가 주어질때, 순회 판매원이 어떤 특정 도시를 출발하여 어떠한 도시도 두 번 방문함 없이 모든 도시를 거쳐 처음 출발한 도시로 돌아오는 경우의 '최소 경로'를 찾는 문제
- 일반적인 해결 알고리즘이 존재하지 않음
- 도시가 많아질 수록 경우의 수가 크게 늘어남 -> NP-hard 문제(NP-complete 보다 어려운 문제)

최단 경로 문제
- 최단 경로 : 가중 그래프에서 가장 짧은 거리의 경로

다익스트라 알고리즘
- 가중치가 모드 음수값이 아닌 방향 그래프에서 주어진 출발점과 도착점 사이의 최단 경로를 찾아주는 알고리즘
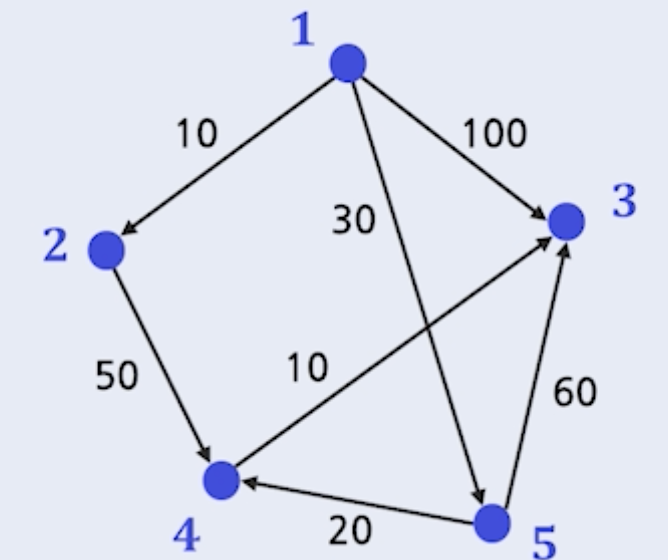
ex) 1에서 2까지 최단 거리는? 1에서 3까지 최단 거리는? 1에서 4까지 최단 거리는?
에츠허르 다익스트라
- 네덜란드 출신 컴퓨터 과학자
- 전산학이 정립되지 않은 시절 전산학의 여러 분야에 기여함
- 다익스트라 알고리즘을 개발하여 최단 경로 문제에 대한 학문적 연구를 시작
- GOTO문 사용하지 말것을 주장
- 세마포어에 대한 연구를 처음 시작함
- 1972년 튜링상 수상

다익스트라 알고리즘의 Pseudo-code
void Dijkstra()
{
S = {1};
for (i=2; i <= n; i = i + 1)
{
D[i] = C[1, i];
// D[i]는 노드 i에서 노드 j까지의 최단 거리
// C[i, j]는 노드 i에서 노드 j까지의 거리
// 노드 i에서 노드 j로 가는 연결선이 없다면 C[i, j] = inf
}
for (i = 1; i <= n - 1; i = i + 1)
{
V - S에 있는 노드 중에서 D[w]가 최소인 노드 w를 선택;
w를 S에 추가;
V - S에 있는 각 노드 v에 대해 D[v] = min(D[v], D[w] + C[w, v]);
}
}
다익스트라 알고리즘의 적용 예시
- 1에서 2까지 최단거리 = 10
- 1에서 3까지 최단거리 = 60
- 1에서 4까지 최단거리 = 50
- 1에서 5까지 최단거리 = 30

그래프의 탐색
1. 탐색 정의
2. 깊이 우선 탐색
3. 너비 우선 탐색
그래프 탐색
- 그래프의 모든 노드를 체계적으로 방문하는 방법
ex) 깊이 우선 탐색, 너비 우선 탐색

메모리 구조
- 스택
- 큐
스택
- LIFO(Last In First Out) 구조를 가지는 메모리 한 형태

큐
- FIFO(First In First Out) 구조를 가지는 메모리 한 형태

깊이 우선 탐색 Depth First Search, DFS 과정
1. 임의의 시작 노드 v를 선택하고 탐색
2. v에 인접한 노드 중
-> 방문하지 않는 노드 w가 있으면 v를 스택에 push하고 w를 방문, 그리고 w를 v로 설정한 뒤 2를 반복
-> 방문하지 않은 노드가 없으면 스택을 pop하여 받은 가장 마지막 방문 노드를 v로 설정한 뒤 2를 방문
3. 스택이 공백이 될 떄 까지 2를 반복
깊이 우선 탐색 과정 예
- A를 우선 탐색 -> 스택
- B를 탐색 -> 스택 A
- D를 탐색 -> 스택 A B
- G를 탐색 -> 스택 A B D
- F를 탐색 -> 스택 A B D G
- F에 인접한 노드가 없음 -> G를 Pop
- E를 탐색 -> 스택 A B D
- C를 탐색 -> 스택 A B D E
- C에 인접한 탐색할 노드 없음 -> E Pop -> 스택 A B D
- D에서 탐색할 노드 없음 -> D pop -> 스택 A B
- B에서 탐색할 노드 없음 -> B pop -> 스택 A
- A에서 탐색할 노드 없음 -> A Pop -> 스택

너비 우선 탐색(Breadth First Search, BFS)
1. 인의의 시작노드 v를 선택하고 이를 탐색한다.
2. v에 인접한 노드 중
- 방문하지 않는 노드를 차례로 방문하여 큐에 enQueue 한다.
- 방문하지 않은 인접한 노드가 없으면 큐에서 deQueue한 노드를 가지고 2를 계속 반복
3. 큐가 공백이 될 때 까지 2를 반복한다.
너비 우선 탐색 과정 예
1. A를 우선 탐색 . v = A
2. B를 탐색 -> enQueue B -> Queue B
3. C를 탐색 -> enQueue C -> Queue B C
4. v에 더이상 인접한 노드 없음 -> deQueue B -> v = B -> Queue C
5. D를 탐색 -> enQueue D -> Queue C D
6. E를 탐색 -> enQueue E -> Queue C D E
7. v(B)에 인접한 노드 없음 -> deQueue C -> v = C -> queue D E
8. v(C)에 인접한 노드 없음 -> deQueue D -> v = D -> queue E
9. G를 탐색 -> enQueue G -> Queue E G
10. v(D)에 인접한 노드 없음 -> deQueue E -> v = E -> queue G
11. F 탐색 -> enQueue G -> Queue G F
12. v(E)에 인접한 노드 없음 -> deQueue G -> v = G -> queue F
13. v(G)에 인접한 노드 없음 -> deQuque F -> V = F -> queue
14. 종료

'수학 > 알고리즘' 카테고리의 다른 글
| 이산 수학 - 16 트리 활용 (0) | 2020.06.08 |
|---|---|
| 이산 수학 - 15 트리 (0) | 2020.06.08 |
| 이산 수학 - 13 그래프 (0) | 2020.06.08 |
| 이산 수학 - 10 관계 (0) | 2020.06.07 |
| 이산 수학 - 2 수의 종류 (0) | 2020.06.07 |