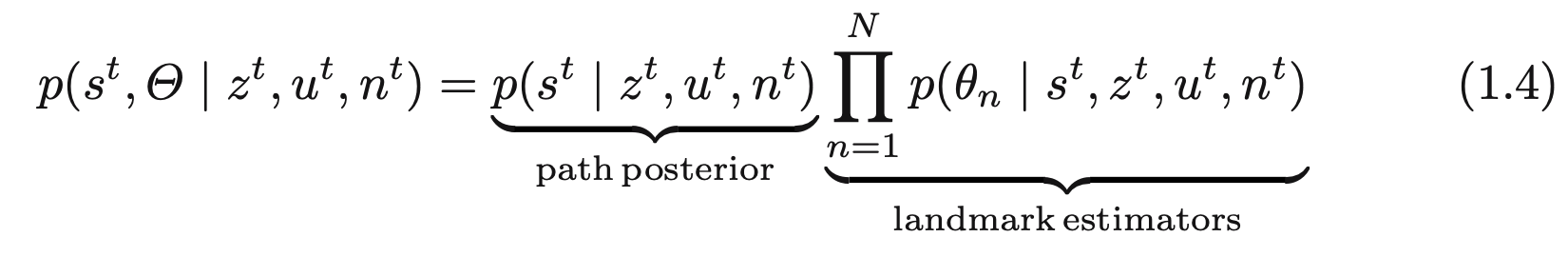집밖은 위험해

2.2 SLAM 사후확률

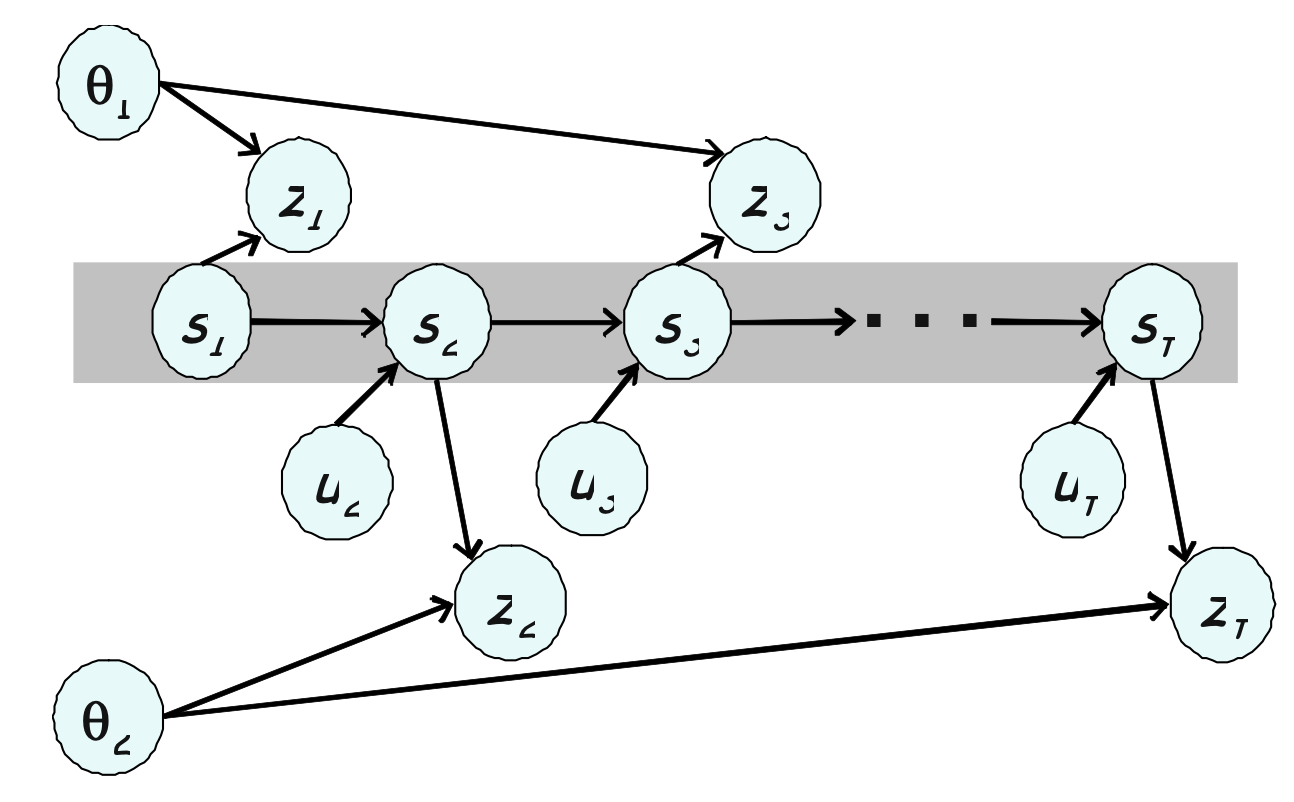
 시간 t에서의 로봇의 자세를 $s_t$라고 하겠습니다. 평면 공간에서 로봇이 주행하면서, 로봇의 자세는 평면 공간에서의 x-y 위치와 해딩각도로 이루어 집니다. 앞으로 살펴볼 모든 실험은 평면 환경에서 수행될 것이나, 어떤 알고리즘들은 3차원 세계에서 다루겠습니다. 로봇의 모든 시간에서의 자세로 이루어진 로봇의 완전한 궤적은 $s^t$라고 쓰며 아래와 같습니다.

 이번에는 로봇의 주위 환경을 N개의 점 랜드마크의 집합으로 설계할수 있습니다. 점 랜드마크는 센서로부터 추출한 특징의 위치로, 레이저 스캔으로 구한 기하학적 특징이나 카메라로 얻은 시각 특징 같은게 될수 있습니다. N개의 랜드마크 위치 집합을 {$\theta_1$, . . ., $\theta_N$}이라고 쓰겠습니다. 전체 지도에 대해서 간단하게 적으면 $\Theta$로 표기하겠습니다.

 로봇은 주위 환경에서 주행하면서, 로봇의 동작에 대해 상대적인 정보들을 수집하는데, 이 정보는 로봇의 바퀴에 장착된 오도미터나, 관성 센서로 구할수 있으며, 아니면 로봇이 수행하는 제어입력으로 구할수 있겠습니다. 원점이 어디인지든 간에 로봇의 동작을 제어 입력이라고 부릅니다. 시간 t에 대한 제어 입력을 $u_t$라 하며, 모든 제어 입력의 집합을 $u^t$라고 표기합니다.

 로봇이 주행하는 동안에 근처에 있는 랜드마크들을 관측도 하는데, 평면 공간에서의 SLAM 문제에서 로봇들은 장애물, 랜드마크에 대한 거리와 방위를 측정하게 됩니다. 이 시간 t에서의 관측을 $z_t$라 하며, 로봇이 수집한 모든 관측 집합을 $z^t$라고 표기합니다.

 SLAM에 있어서 센서 관측치들은 개별적인 랜드마크에 대한 정보로 분할하여 다룰수 있는데, 각 랜드마크 관측치는 다른 간측치로부터 독립적으로 반영할수 있습니다. 이는 성공적으로 SLAM을 구한하기 위해서 가공되지 않은 센서 데이터로부터 랜드마크 특징들을 하나 하나 추출하는데 있어, 현실적인 가정이라 할 수 있겠습니다. 그래서 각각의 관측은 로봇의 현재 자세 $s_t$에 대해 상대적인 랜드마크의 위치 $\theta_n$에 대한 정보를 전달한다고 할수 있겠습니다. 

 여기서 변수 n은 관측된 랜드마크의 아이디로, 현실에서는 많은 수의 랜드마크들이 비슷비슷하게 생겨서, 랜드마크의 아이디는 관측할수 없습니다. 관측 $z_t$로 얻은 랜드마크의 아이디를 $n_t$라고 표기하겠습니다.($n_t$ $\in$ {1, . . .N}). 예를들어 $n_8$ = 3이라고 한다면, 시간 t=8에 로봇이 관측한것이 3번째 랜드마크라는 의미가 되겠스빈다. 랜드마크 아이디를 보통 데이터 연관 data associations이나 대응관계 correspondences라고 부릅니다. 이러한 모든 데이터 연관 집합을 $n^t$로 표기합니다.

 쉽게 보자면, 로봇은 매 시간마다 제어입력 $u_t$를 수행하고, 관측 $z_t$를 얻는다고 할수 있겠습니다. 시간 t에서 다중 관측치또한 처리될수 있겠으나 조금 복잡한 표기를 해야되겠습니다.

 위의 정의들을 사용하여 SLAM의 주요 목표는 노이즈를 가진 관측치들 $z^t$와 제어 입력들 $u^t$이 주어질때, 로봇의 자세 $s_t$와 지도 $\Theta$의 최고의 추정치를 구하는것이라 할수 있겟습니다.

 확률적인 용어로 이는 아래의 사후확률로 표현할 수 있겠고,

 모든 데이터 연관에 대한 집합 $n^t$가 주어진다면, 이 사후확률은 다음과 같이 고칠수 있겠습니다.

 이번에는 동시적 위치 추정 및 지도 작성 Simultaneous Localization and Mapping SLAM에대한 개요를 살펴볼 것이고,

우선 확장 칼만 필터에 기반한 알고리즘에 대해서 소개하겠습니다.

2.1 문제 정의

 이동 로봇이 모르는, 정적 환경에서 주행중이라고 생각해봅시다. 로봇은 제어 입력들을 수행하고, 주위 환경에 대해 관측을 하게 될 것입니다. 제어와 관측은 둘다 노이즈로 훼손되는데, SLAM은 이런 노이즈를 가진 제어입력과 관측치 집합으로부터 로봇의 경로와 주위 지도를 생성하는 처리과정이라 할수 있겠습니다.

 로봇의 경로를 알고있다면, 지도 작성은 간단한 문제가 되어 주위 환경에 존재하는 물체의 위치를 독립적인 필터로 추정할수 있을 겁니다.

하지만 로봇의 경로를 알지 못할때 로봇의 경로에서 존재하는 에러가 지도 상에 존재하는 랜드마크의 위치 오차에 영향을 주게되므로 로봇과 지도의 상태는 동시적으로 추정되어야만 합니다.

 로봇의 자세 에러와 지도 에러 사이 상관관계는 그림 2.1(a)의 그래프에서 볼수있겠습니다. 로봇은 점선 경로를 따라 이동하면서, 주위에 원으로 그려진 랜드마크들을 관측할 것입니다. 여기서 그림자 타원은 시간 변화에 따른 로봇의 자세에 대한 불확실성을 보여주고 있습니다. 제어 에러로 인해 로봇의 자세는 로봇이 움직일 수록 더 큰 불확실성을 가지게 됩니다. 랜드마크 자세의 추정치는 그림자없는 타원으로 나타나고 있는데, 로봇의 자세가 불확실해지기 때문에 관측된 랜드마크 위치 추정치의 불확실성 또한 증가하게 됩니다.

  그림 2.1 (b)에서는 로봇은 루프를 닫고, 이전에 관측한 랜드마크를 재방문하였습니다. 첫번쨰 랜드마크의 위치를 높은 정확도로 알고있기 때문에, 로봇의 자세 추정치의 불확실성은 크게 줄어들게 됩니다. 로봇 자세에 대한 이러한 새로운 정보의 발견으로 이전 로봇 자세에 대한 확실도 또한 파악할수 있게 됩니다. 이를 통해 로봇이 이전에 관찰했던 랜드마크들의 불확실성 또한 줄어듭니다.

 이 글을 보는 분들은 그림 2.1 (b)에서 루프 폐쇄전에 그림자 타원이 줄어들지 않는것을 알 수 있는데, 이는 로봇의 자세 불확실성을 보여주고 로봇의 이전 자세 추정치가 수정되지 않았기 때문입니다.

 루프 주위에 있는 모든 랜드마크를 관측한 영향들은 SLAM 문제에서 상관성의 결과라고 할수 있겠습니다. 지도에서의 오차는 로봇의 경로에서의 오차와 관련되고, 로봇의 자세에 대한 정보를 알려주는 관측이 이전에 관측한 모든 랜드마크에 대한 정보들 또한 전달하게 됩니다.

(a) 루프 폐쇠전 : 로봇 자세 불확실성이 커짐에 따라 랜드마크의 불확실성또한 증가하고 있습니다. 시간 변화에 따른 로봇의 자세 추정치는 그림자 타원이며, 랜드마크 추정치는 그림자없는 타원이 보여주고 있습니다.

(b) 루프 폐쇄후 : 이미 알고있는 랜드마크를 다시 방문하는것으로 로봇의 자세 불확실성을 낮춰주고, 이전에 관측된 랜드마크의 불확실성 또한 줄여줍니다.

그림 2.1 로봇 동작 에러와 지도 에러의 상관관계

FastSLAM 알고리즘

 Fast SLAM은 표 1.1처럼 4단계로 주어진 제어와 관측치를 이용해 파티클 필터를 재귀적으로 갱신 합니다.

첫 번째 단계는 이전 자세와 새 입력을 이용하여 각 파티클에 대한 로봇의 세로운 자새를 구합니다.

다음으로, 최근 관측치와 함께 각 파티클에서의 랜드마크 필터는 표준 EKF 갱신 식을 사용하여 갱신 됩니다.

각 파티클에는 중요도 가중치를 할당하고, 이 가중치에 따라 새로운 샘플들을 생성합니다.

중요도를 이용한 리샘플링 단계를 통해 제안 분포와 사후 확률 분포 사이의 차이를 갱신하여 줍시다.

 이 갱신 과정은 샘플의 수가 무한에 가까울수록 실제 사후확률 분포에 가까워 지지만

실제로는, FastSLAM 사용시에 상대적으로 적은 파티클 (M = 100)만 하더라도 좋은 사후확률을 구할수가 있겠습니다.

 로봇의 경로를 사용하여 슬램 사후확률을 분해하는것은 경로의 길이가 시간에 따라 커지므로 좋지 않은 선택처럼 보일수 있으며, 로봇의 경로에 대한 사후확률 추정시 필터의 차원이 시간에 따라 더 증가할거라고 볼수도 있습니다.

 하지만  FastSLAM에서는 그렇지 않은데,

랜드마크 갱신 식과 중요도 가중치는 최신 로봇의 자세에만 의존하므로

이전의 로봇 경로에 대한것을 잃어버려도 상관없기 때문입니다.

 그 결과 FastSLAM의 각 파티클들은 현재 로봇의 자세에 대한 추정치만 유지하면 되고, 파티클 필터의 차원수가 시간이 지나더라도 고정되어 집니다.

1.6.1 로그 복잡도

 FastSLAM은 EKF보다 두가지 주요한 장점을 가지고 있습니다.

첫째로, 지도에 대한 추정을 분해하여 로봇의 경로가 주어질때 각 랜드마크 사후확률을 추정하는것으로 함으로써

FastSLAM은 효율적으로 완전 슬램 사후확률을 계산할수 있게 됩니다.

 동작 갱신과 관측 갱신, 그리고 중요도 가중치 계산은 모두 파티클 하나당 상수 시간에 수행할 수 있게 됩니다.

리샘플링 단계는 순수한 FastSLAM으로 구현한다면, 선형 시간에서 수행될 수 있지만

 로그 시간을 수행하도록 구현할수도 있는데,

랜드마크 추정기를 배열 대신 이진 트리의 형태로 각 파티클들을 구성하면 됩니다.

1.6.2 다중 가정 데이터 연관

 로봇 경로에 대한 샘플링은 올바른 데이터 연관을 수행하는데 중요한 영향을 줍니다.

FastSLAM에서 각 파티클은 특정한 로봇의 궤적을 나타내기 때문에,

각각의 파티클에 대해 동일한 정보 연관이 수행될 필요는 없습니다.

 FastSLAM에서 데이터 연관 결정은 각 파티클에 기반하여 만들어 지는데,

올바르게 정보 연관을 하는 파티클은 높은 가중치를 받을 것이고, 이후 리샘플링 될 확률이 더 커질것입니다.

 하지만 잘못된 데이터 연관을 수행한 파티클은 적은 가중치를 받을것이고, 이후 사라질것입니다.

데이터 연관으로 샘플링을 하는것으로 FastSLAM이 새로운 증거가 생길때, 이전의 데이터 연관을 고칠수 있게 해줍니다.

 이 과정은 랜드마크의 추가나 제거시에도 동일하게 수행됩니다.

종종, 각 파티클의 데이터 연관은 파티클들이 랜드마크의 갯수가 다른 지도를 만드는 상황을 만들기도 합니다.

 이로 인해 가장 높은 확률의 지도를 계산하기 어렵게 만드나,

FastSLAM이 더 확실한 근거가 쌓일때 잘못된 랜드마크를 제거할수 있도록 해줍니다. 

 어느 관측치가 특정 파티클에서 새로운 랜드마크를 생성시켜버리나

다른 관측치들은 이 관측이 이미 존재하는 랜드마크에 속한다고 판단한 경우에

새로운 랜드마크를 생성해야한다는 파티클은 적은 가중치를 가지게 될 것이고,

이후 리샘플링 단계에서 올바르지 않은 파티클이 사라지면서 이전에 생성된 랜드마크도 제거될것입니다.

1.7 개요

 이 자료를통해 FastSLAM 알고리즘의 전반에 대해서 살펴볼것이고,

다양한 시뮬레이션과 실제 환경에서 얻은 데이터 셋으로 FastSLAM과 EKF의 성능을 비교해보겠습니다.

 2장에서 SLAM문제를 공식화하고, EKF 기반 선행 방법들에 대해 주로 다루어보겠습니다.

 3장에서 데이터 연관이 주어지거나 주어지지 않은 경우 둘다에 대해 가장 간단한 버전의 FastSLAM도 살펴봅시다.

FastSLAM 1.0이라고 하는 버전은 구현하기 가장 간단한 FastSLAM 알고리즘으로, 일반적인 SLAM 환경에서도 잘 동작합니다.

 4장에서는 기존의 FastSLAM의 개선된 버전인 FastSLAM 2.0을 볼것인데, 기존의 것보다 더 좋은 결과를 보여줍니다.

이 알고리즘은 현재 관측을 파티클의 제안 분포에 반영하여, 결과적으로 동작 노이즈가 센서 관측보다 큰 경우에 더 정확한 결과를 계산할수 있게 만들어 줍니다.

 5장에서는 SLAM 문제와 같은 구조인 동적 물체 추적 문제를 살펴볼 것이고, 어떻게 FastSLAM 알고리즘의 바리에이션을 이용하여 정밀하게 위치 추정되지 않은 로봇으로 부터 동적인 물체를 추적하는지 살펴보겠습니다. 

1.6 FastSLAM

실제 로봇의 주행 궤적과 랜드마크 사이의 관계 

 1.2 결합 추정에서 지도의 요소들 사이 상관관계는 로봇의 자세 불확실성에서 발생하는것을 봤었습니다.

그래서 실제 로봇의 주행 궤적을 안다면 랜드마크 위치들을 독립적으로 추정할수 있겠습니다.

로봇의 실제 궤적을 아는것으로 랜드마크 위치 추정은 조건부 독립이 된다고 할 수 있습니다.

 이 내용에 대한 증거로 아래의 그림 1.5와 같이 동적 베이지안 네트워크로 슬램 문제를 보면 확인 할 수 있습니다.

 시간 t에 대한 로봇의 자세를 $s_t$로 이 자세는 이전의 로봇 자세 $s_{t-1}$과 제어 $u_t$를 실행하여 얻을 수 있습니다.

시간 t에 대한 관측은 $z_t$로 표기하며 로봇의 자세 $s_t$와 관측된 랜드마크 $\theta_{n_t}$로 얻을 수 있습니다.

 위 그림의 시나리오 데로 따라가면 랜드마크 1은 t = 1, 3일때 관측되며, 랜드마크 2은 t=2에서 관측됩니다.

회색 공간은 로봇의 전체 경로를 강조하고 있습니다.

 이 네트워크를 보면 알수 있지만 이 경로는 두개의 랜드마크를 나타내는 노드로 나누어지게 됩니다.

정리하면 로봇의 실제 주행 경로를 알고 있는 상태에 첫번째 랜드마크의 위치를 안다고 해서

두번쨰 랜드마크의 위치를 구하는데 도움되지 않는다고 할수 있습니다.

랜드마크간 조건부 독립을 이용한 SLAM 사후확률 분해

 이 관계를 통해서, 데이터 연관이 주어질때 SLAM 사후확률은 다음의 곱 형태로 구할수 있겠습니다.

 이 분해를 통해 완전 SLAM 사후확률이 N + 1개의 재귀 추정기로 나눌수 있음을 알수 있으며,  1개 추정기는 로봇의 경로에 대한 것이고,

N개의 로봇의 경로 추정에 조건부이며, 서로의 랜드마크 위치에독립적인 추정기들로 이루어집니다.

 위 분해된 사후확률은 파티클 필터를 이용하여 효과적으로 근사화 할수 있으며, 이 파티클 필터의 파티클들은 로봇의 샘플 경로가 됩니다.

여기서 각 파티클들은 N개의 독립 랜드마크 추정기에 붙여져(EKF로 구현됨), 해당 랜드마크에 대한 로봇의 자세가 되겠습니다.

 랜드마크 필터들이 각각의 랜드마크의 자세를 추정하므로, 각 필터는 저차원이 되겠습니다.

그래서 전체적으로 N x M개의 칼만 필터가 사용됩니다.

이 파티클 필터를 갱신하는 알고리즘을 FastSLAM이라 부르겠습니다.

 통계학에 친숙한 사람이라면 이 FastSLAM이 Rao-Blackwellized Prticle Filter를 구현한 것임을 알수 있을 겁니다.

관측과 제어 사이 제약

 주어진 시간에 대해 누적된 관측과 제어들은 상태 변수들의 일부 부분집합을 제약하며,

데이터와 상태 변수 간에 의존관계에서 이러한 희소성은 슬램 사후확률 계산을 더 효율적으로 하도록 사용할수 있습니다.

상관관계와 부분 지도

 예를들어 서로 멀리 떨어진 두 랜드마크는 약한 상관 관계를 가지며,

다른 멀리 떨어진 랜드마크 쌍 또한 비슷하게 약한 상관관계를 가지게 됩니다.

많은 EKF SLAM 알고리즘은 이러한 성질을 사용하여 전체 지도를 작은 부분집합 지도로 나누어 사용합니다.

EKF 분해

 큰 EKF를 많은 수의 느슨하게 결합된 작은 EKF로 나눌수 있겠습니다.

이 방법은 EKF 근사 알고리즘이 선형 시간에 수행되고,

관측 반영이 상수 시간에 수행될수 있도록 하는 장점을 가지고 있습니다.

 슬램 문제를 희소하도록 분해함으로서 효율적인 EKF 기반 알고리즘을 만들수 있고,

이 새 알고리즘은 기존의 EKF 처럼 데이터 연관시 동일한 어려움을 직면하게 됩니다.

데이터 연관 개선 방안

 앞으로 상태 변수들 간에 의존관계에서 희소성을 이용하여 이 문제를 개선한 방법을 볼것이고,

슬램 사후확률 계산을 효율적으로 할수 있도록 이 방법은 다중 데이터 연관 가정을 사용하겠습니다.

이를 통해 큰 데이터 연관 애매함을 가진 넓은 환경에서도 사용가능한 슬램 알고리즘을 얻을 수 있습니다.

1.4 확장칼만필터

확장 칼만 필터의 SLAM 적용

 SLAM 문제에 대한 접근방법은 1986년 스미스와 치즈만의 논문에서 소개되었으며,

몬타리어와 카틸라가 이 시스템을 최초로 구현하였습니다.

이들은 지도와 로봇의 자세에 대한 사후확률을 추정하기 위해서 확장칼만필터 EKF를 사용하였습니다.

확장 칼만 필터의 공분산과 예시

 확장 칼만필터는 슬램 사후확률을 지도상에 존재하는 모든 특징과 로봇의 자세에 대한

고차원 가우시안으로 근사화를 시킵니다.

 이 다변수 가우시안 공분산 행렬의 비대각 요소는 상태변수 쌍의 상관관계를 가지고 있습니다.

모든 쌍 상태 변수를 나타내는 공분산을 근사화하여, EKF는 상관 에러를 효과적으로 나타낼수 있습니다.

 아래의 좌측 그림은 시뮬레이션된 데이터를 사용하여 EKF를 수행한 결과를 보여주고 있으며,

여기서 타워은 랜드마크 위치 불확실성을 나타내고 있습니다.

 우측 그림은 상관 관계를 나타내는 공분산 행렬이며,

행렬 요소가 검을수록 대응되는 상태변수 간의 상관관계가 더 커지게 됩니다.

EKF의 주요 문제점

 EKF는 슬램의 주요 방법이 되었지만, 현실 세계에서 넓은 공간에 적용하기에는 두 가지 중요한 문제점을 가지고 있습니다.

- 이차 복잡도와 데이터 연관 실패 민감도

1.4.1 이차 복잡도

 EKF로 SLAM 문제를 다룰때 첫 번째 결점은 계산복잡도입니다.

지도에 존재하는 랜드마크의 수에 따라 EKF 사용시 계산 시간과 메모리 둘다 이차적으로 필요하게 됩니다.

 이차 복잡도는 EKF을 가우시안 표현법을 사용하기 때문인데,

슬램 사후확률 불확실성은 모든 상태변수들간의 상관관계로 이루어진 공분산행렬로 나타냅니다.

 2차원에서 이 공분산 행렬은 (2N + 3) x (2N + 3) 개의 요소를 가지고 있어(N은 전체 랜드마크의 수)

공분산 행렬을 저장하기 위한 메모리가 N^2으로 증가하게 됩니다.

1.4.2 단일 가정 데이터 연관

 EKF 기반 슬램 방법의 두 번재 문제는 데이터 연관으로,

데이터 연관은 측정과 랜드마크 사이에 대해 다룹니다.

 슬램 문제에서  정보 연관이 주어진 경우 쉽게 식으로 정리할 수 있겠지만,

실제 세계에서 관측치와 랜드마크 사이 연관 관계는 숨겨진 변수로서

로봇의 자세와 랜드 마크를 추정하기 위해 찾아내어야 합니다.

기본적인 정보 연관 방법

 EKF에서 정보 연관을 위한 기본적인 방법은 모든 관측치를 최대 우도를 사용하여 랜드마크로 정하는 것입니다.

여기서 모든 관측치는 가장 가능성 있는 랜드마크로 판단됩니다.

만약 관측이 존재하는 랜드마크일 확률이 너무 낮으면, 새 랜드마크로 판단 합니다.

잘못된 정보가 반영시

 EKF는 정보 연관시 불확실성을 나타내는 방법이 없기 때문에

잘못된 정보 연관이 주어질때의 관측치가 반영될수 있습니다.

수많은 관측치가 잘못되어 EKF에 반영되면, 필터는 벗어나 실패하게 됩니다.

다중 데이터 연관의 한계

 EKF의 데이터 연관 정확도는 다중 연관 통해 개선시킬수 있으나

이 방법 또한 EKF 내부적으로 각각의 단일 가정을 사용한다는 문제가 있으며

처음 관측한 데이터가 가장 가능성 있는 것을 골랐다고 해도 항상 올바른 데이터 연관을 했다고 할수 없고,

잘못된 데이터 연관을 통해 실제 연관 관계를 계속 찾을수 없을수도 있습니다.

  다중 데이터 연관 가정은 EKF 여러개를 사용하는 것이며, 각 마다 하나의 데이터 연관 가정을 다룬다고 볼수 있습니다.

하지만 이렇게 한다면 EKF로 SLAM을 하기에는 계산량이나 메모리량이 부족하여 실행할수 없게 됩니다.

1.3 사후 추정

로봇이 사용가능한 정보

 시간에 따라 로봇에서 사용가능한 두 가지 종류의 정보들이 존재합니다.

이 정보들은 제어 입력과 관측치로, 제어 입력은 로봇의 동작을 예측하는데 사용하는 노이즈를 가진 입력이며

관측치들은 로봇 주위에 존재하는 물체들에 대한 노이즈를 갖고 있는 측정치를 말합니다.

정보의 노이즈와 정보들 간의 제약조건

 제어 입력과 관측치 각각은 올바른 노이즈 모델과 결합되어 있으며, 확률적은 제약조건으로 볼수 있습니다.

하지만 관측치는 지도에서 로봇의 위치와 물체 사이의 상대적인 제약을 가지고 있습니다.

 이전에 관측한 특징을 다시 재방문한다면,제약조건은 지금 관측한 특징과 로봇의 자세 뿐만이아니라

이전에 보았던 올바른 특징들까지 갱신시켜버릴 것입니다.

제약 네트워크와 SLAM의 목표

 제어와 관측 정보로 만들어지는 제약 네트워크 예시는 아래의 그림 1.3과 같겠습니다.

처음에는 제어와 관측간의 제약은 상대적으로 약할수 있지만, 지도 특징이 반복해서 관측된다면 이 제약은 더 강해질 것입니다.

 관측과 제어의 수는 제한되며, 지도에 존재하는 모든 특징들의 위치는 서로 완전 상관관계를 가지게 됩니다.

SLAM의 주요 목표는 사용가능한 제어와 관측치가 주어지면 이를 통해 로봇의 진짜 자세와 지도를 추정해 내는것이 됩니다.

그림 1.3 관측과 제어는 로봇의 자세와 특징들 사이의 확률적 제약 네트워크를 만듭니다. 이 제약들은 위와 같은 두꺼운 선으로 나타납니다.

SLAM 문제의 한 방법과 한계

 SLAM 문제를 다루기 위한 한가지 방법으로 배치 추정 알고리즘을 사용하여

가장 가능성 있는 로봇의 자세와 지도를 추정하는 방법이 있습니다.

 이 방법은 효과적일수 있으나 완천한 관측치와 제어 집합이 주어질때 사용할수 있는 기술로,

그 결과 온라인 연산시에는 사용하기 부적절 합니다.

온라인 SLAM과 사후확률

 SLAM을 온라인으로 다루기 위한 방법은 모든 제어 입력 $u^t$와 관측 $z^t$가 주어질때,

모든 가능한 지도 $\Theta$와 로봇의 자세 $s_t$에 대한 사후 확률 분포를 추정하는것입니다.

지도와 로봇의 자세에 대한 결합 사후확률은 다음과 같이 표기합니다.

 위 확률 분포를 SLAM 사후 확률이라 부르며, 얼핏 보기에 사후확률 근사는 배치 추정 방법보다 불가능한것 처럼 보있수 있습니다.

온라인 SLAM 사후 확률 추정의 이점들

 하지만 몇가지 가정을 사용하면 SLAM 사후확률을 효율적으로 계산할 수 있으며,

가장 가능성 있는 해들에 대한 사후확률 추정은 많은 이점을 가지고 있습니다.

1. 가능한 해들에 대한 확률 분포로 노이즈가 많은 호나경에서 더 강건한 알고리즘을 만들 수 있습니다.

2. 해의 다른 요소로 얻을수 있는 정보와 비교하는데 불확실도를 사용할 수 있습니다.

한 지도의 어느 부분은 매우불확실하더라도 다른 부분들은 확실할수 있습니다.

지도를 나타내는 특징들

 지도에 대한 모수화된 모델을 $\Theta$로 표기하며, 이들은 일반적으로 점 특징, 랜드마크의 집합으로 나타납니다.

실제 구현시 랜드마크들은 센서 측정으로 추출된 특징들의 위치에 해당하며, 앞으로 점 랜드마크 모델과 다른 표현방식들을 살펴보겠습니다.

선 세그먼트 같은 고차 기하학적인 특징들 또한 SLAM에서 지도 표현에 사용되기도 합니다.

정보 연관

 완전 슬램 사후확률은 관측치와 지도 특징들간의 상관관계를 모른다고 가정하며,

랜드마크들을 유일하게 구별할수 있다고 가정한다면 SLAM 사후확률을 아래와 같이 정리할 수 있습니다.

 여기서 $n_t$는 시간 t에 관측된 랜드마크의 식별자이며,

$n^t$는 시간 t에 관측된 모든 랜드마크들의 식별자 집합이라고 할수 있습니다.

이 대응 관계 집합 $n^t$는 다른말로 정보 연관이라고 부르기도 합니다.

SLAM과 베이즈 필터

 앞으로 살펴볼 SLAM 문제들은 정보 연관이 주어진 경우와 더 일반적인 SLAM 문제들을 살펴보겠습니다.

이후에는 정보 연관 제약이 다중 정보 연관 과정을 사용하여 어떻게 완화되어지는지도 보겠습니다.

 다음의 재귀식을 SLAM 문제에 베이즈 필터를 적용한 것으로 추후 자세히 살펴보겠습니다.

 위 식에서 적분은 닫힌 형태로는 계산할수 없으나, 사후확률 분포에 대한 특정한 형태로 가정하면 계산할수 있습니다.

특히 많은 통계적 추정 기술들, 칼만필터나 파티클 필터 같은 방법들이 이런 일반 베이즈 필터를 쉽게 근사화 시킬수가 있겠습니다.

1. 소개

SLAM의 중요성

 SLAM이라 부르는 로봇공학에서의 문제는 많은 관심을 받고 있습니다.

SLAM에서는 사전에 지도와 같은 주위 환경에 대한 정보 없이 로봇이 이동하는 문제를 다루는데요.

로봇은 노이즈의 영향을 받는 동작에 따라 주위 랜드마크를 관측하여 다양한 상대적인 관측치들을 만들어 냅니다.

SLAM의 목표는 로봇의 주행 경로와 이를 따라 지도를 만들면 됩니다.

그리하여 SLAM은 자율 주행 분야에서 가장 핵심적인 선수과제가 되었습니다.

왜 SLAM이라 부르나?

 만약 주위 환경에 대한 실제 지도가 사용가능하다면 바로 위치 추정 문제로 다룰수 있고,

로봇의 실제 주행 궤적을 알고 있다면 지도 작성은 쉽게 수행할수 있습니다.

하지만 로봇의 주행 경로와 지도를 둘다 모를때는 위치 추정과 지도 작성은 동시에 고려해야할 문제이며

그래서 동시적 위치 추정 및 지도작성 SLAM이라고 부르게 되었습니다.

1.1 SLAM 응용

실외 환경에서 SLAM의 필요성

 SLAM 기술은 이동 로봇이 전역 정밀 위치 데이터(GPS같은)를 사용하지 못하는 잘 모르는 환경에서 주행할때 필수적입니다.

특히 위험하거나 아주 멀거나, 사람이 가기 힘든 그러한 곳으로 이동 로봇은 원격으로 돌아다닐수 있어야 하고,

로봇이 심해나 지하, 다른 행성과 같은 극한의 환경에서 스스로 돌아다니기 위해서 주위 환경에 대한 지도를 작성하고 이 지도를 이용해서 주행할수 있는 능력을 가져야만 합니다.

실내 환경에서 SLAM의 필요성

 건물 실내와 같은 환경에서 또한 그러한 지도를 얻기 힘들수도 있습니다.

모르는 공간에 대한 지도를 만드는 능력을 가지고 있으면 로봇은 적은 장비로도 효율적으로 사용할수 있을겁니다.

특히 시간에 따라 주위 환경이 변하는 곳에서 이러한 능력이 훨씬 중요합니다.

SLAM 수행 환경 예시

 SLAM 알고리즘으로 작성한 지도는 로봇의 주행 계획과 탐사에서 중요한 기초 자료로 사용되나, 어떤 지도들은 저작권을 갖고 있습니다.

SLAM 실험을 한 대표적인 장소로 심해나 지하, 다른 행성 등이 있겠습니다.

1.2 결합 추정

SLAM에서의 위치 추정과 지도 작성사이의 관계

 위치 추정과 지도 작성 사이은 달걀이 우선이냐 닭이 우선이냐의 관계를 가지고 있으며,

매번 로봇의 동작과 센서 측정의 노이즈로 인한 에러가 반영됩니다.

 로봇이 이동할때 로봇의 추정 자세는 동작 노이즈로 훼손되며,

주위 물체에 대한 위치 또한 로봇의 측정 노이즈와 위치 추정시 발생한 에러로 훼손됩니다.

 하지만 관측 노이즈와는 달리 로봇의 자세에서 에러는 지도 작성에 있어서 심각한 영향을 주게 됩니다.

일반적으로 이 영향을 "로봇의 경로 에러와 지도 에러의 상관관계"라고 할수 있겠는데,

 올바른 로봇의 주행 경로 없이 올바른 지도또한 얻을수 없다는 말이 됩니다.

이러한 위치 추정과 지도 작성 사이 관계에 대한 개념을 1986년 세미나에서 스미스와 치즈먼이 처음으로 제시하였습니다.

잘못된 경로가 주어진 경우 지도 작성과 SLAM을 통한 지도작성 결과 예시

 아래의 그림 1.2는 이동 로봇이 실내 환경에서 주행하면서 레이저 거리 스캔들 한 결과를 보여주며,

로봇은 오도메트리 정보를 이용해서 자신의 위치를 추정하고 있습니다.

 그림 (a)는 로봇의 위치 추정치에 따라 레이저 스캔들을 플로팅한 결과를 보여주고 있으나,

로봇의 오도메트리에는 에러들이 누적되어있으므로 지도의 부정확도가 증가하는모습을 볼수 있습니다.

 그림 (b)의 경우 SLAM알고리즘을 통해 구한 로봇의 경로를 이용하여 지도를 작성한 결과를 보여주고 있습니다.

로봇의 경로 에러와 지도 에러 사이의 관계가 SLAM 문제를 풀기 더 힘들게 만들기도 하나

SLAM이라는 큰 문제를 작은 문제들로 분해하여 처리할수 있으며, 각각의 작은 문제들은 보다 효율적으로 풀수 있을겁니다.

그림 1.2 지도 경로 에러와 지도 에러 사이의 상관 관계