728x90
선형 사상
- f는 n차원에서 m차원으로의 사상
- 아래의 두 조건을 만족한 경우 사상 f는 n차원에서 m차원으로 선형 사상이라 한다.
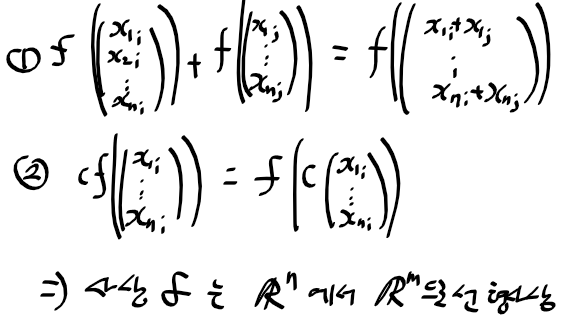
선형 변환
- 선형 변환(1차 변환) : n차원에서 n차원으로 선형 사상
선형 사상과 행렬
- 사상 f는 행렬 m x n와 같은 의미를 갖는다.
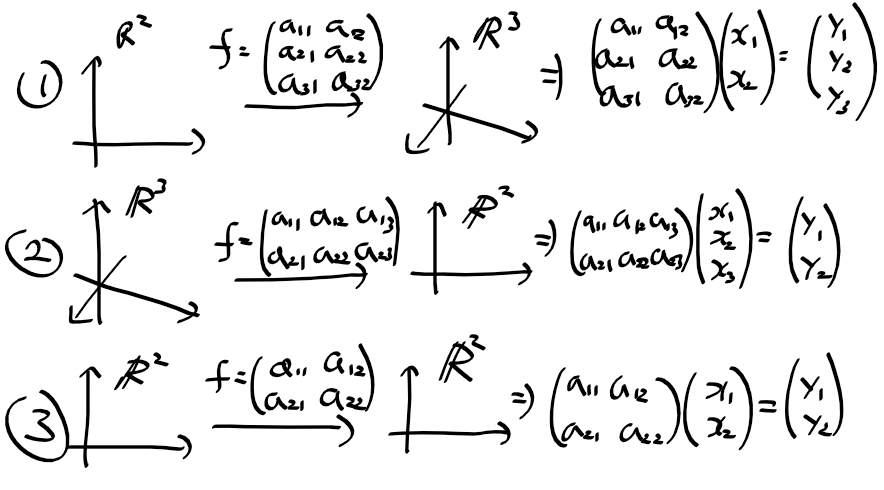
R^n에서 R^m으로 선형 사상

상
- 사상 f에 의해 x_i에 대응하는 집합 Y의 원소
-> 사상 f에 의한 x_i의 상
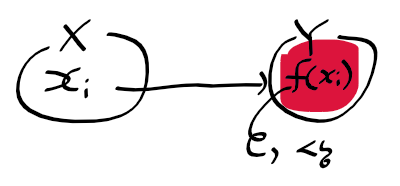
상과 차원 변환
- 선형 대수를 통해 쉽게 상의 변화를 파악 가능
- n차원이 행렬 m x n를 곱하여 m차원으로 변환

300x250
'수학 > 선형대수, 최적화' 카테고리의 다른 글
| 최적화 - 1. 최적화와 관련 개념들 (0) | 2020.07.16 |
|---|---|
| 선형대수 - 고유값과 고유벡터, 추가 (0) | 2020.05.04 |
| 선형대수 - 벡터 (0) | 2020.05.03 |
| 선형 대수 - 행렬 (0) | 2020.05.02 |
| 만화로 쉽게 배우는 선형대수/물리 (0) | 2020.05.02 |