[통계기반학습개론] 5.1.4 K 폴드 교차검증의 편향-분산 트레이드 오프 ~ 5.2 부트스트랩

5.1.4 K 폴드 교차검증의 편향-분산 트레이드 오프

 

 5.1.3에서 언급하다시피 k < n인 k-폴드 교차검증은 LOOCV보다 계산에 있어서 이점을 가지고 있는데, 계산 이점 이외에도 LOOCV보다 테스트 에러를 더 정확하게 구할수 있다는 장점이 있습니다. 이 이유는 편향 분산 트레이드 오프와 관련이 있다.

 

 5.1.1에서 검증셋 방법의 경우 전체 데이터셋의 절반을 훈련 셋으로 사용하고 나머지 절반을 검증 셋으로 사용하다보니 실제 테스트 에러율을 과대추정 한다고 했었다. LOOCV는 n - 1개의 데이터를 훈련셋으로 사용하다보니 테스트 에러율의 불편향적인 추정량 unbiased estimates of the test error을 구한다고 볼수 있겠다

 

 k = 5/10인 경우의 k-폴드 교차검증을 하는 경우에는 훈련셋은 (k - 1)n/k 개로 LOOCV보다는 적지만, 검증 셋 방법에서 전체의 절반을 훈련셋으로 사용한것보다는 많다. 그러므로 편향 축소의 관점에서 본다면 LOOCV는 k-fold 교차 검증보다는 더 낫다고 볼수 있겠다.

-> LOOCV는 대부분의 학습 셋가지고 추정을 하다보니 

(k - 1) n / k개를 가지고 학습하는 k-fold보다 더 정확, 더 적은 편향, 불편향 추정량을 구한다.

-> k-fold 한 모델은 LOOCV보다 적은 데이터를 가지고 학습하므로 편향적인 추정량을 구한다.

 

 하지만 추정 과정에서는 편향 말고도 분산/변동이 얼마나 큰지도 고려하여야 한다. LOOCV는 k-폴드 교차검증보다 변동이 더 크다고 할수 있는데, 왜 그럴까? 한번 LOOCV를 수행하면 n개의 훈련된 모델들의 결과를 평균으로 구하였었는데 이 n개의 모델들은 n - 1개의 데이터로 학습하다보니 실제와 거의 동일한 데이터셋으로 훈련되었었다. 그래서 이 모델의 결과들은 매우 상관관계를 가지며/서로서로 비슷할수 밖에 없다.

 

 하지만 k-폴드 교차검증의 경우 각 모델의 훈련셋의 겹치는 부분이 LOOCV보다는 적다보니, 각 모델들끼리 상관관계를 덜 가지는 모델들의 출력을 평균으로 구한다. 상관관계가 큰 값들로 평균을 구한 경우 덜한 경우로 평균을 구한것 보다 변동/분산이 더크다보니, LOOCV가 k-폴드 교차검증으로 테스트 에러 추정량을 구한것보다 더 큰 변동/분산을 가지게 된다.

-> LOOCV의 학습에 사용하는 데이터셋은 전체 데이터셋에 가깝다보니 변동에 잘 대처를 하지못함 -> 더 큰 분산

-> K-폴드 CV는 각 모델들의 훈련셋이 겹치는 부분이 LOOCV보다 훨씬 적음 -> 다양한 모델들 -> 더작은 분산

 

 정리하자면 편향-분산 트레이드오프는 k-폴드 교차검증에서 k를 무엇으로 지정하느냐에 따라 달린 문제인데, 이런 것들을 고려해서 k = 5 혹은 k = 10을 지정한경우 테스트 에러율은 아주 큰 편향이나 아주 큰 분산/변동의 영향을 덜 받게 된다.

 

 

 

 

5.1.5 분류 문제에서의 교차 검증 Cross-Validation on Classification Problems

 

 이번 장에서는 회귀 문제에서 출력 Y가 양적 변수인 경우의 교차 검증을 사용하였고, 테스터 에러의 척도로 MSE를 사용하였다. 하지만 교차 검증은 Y가 질적 변수인 분류 문제에서도 유용하게 사용할 수 있는데, 테스트 에러율을 구하는데 MSE 대신 오분류 횟수를 사용하여 측정할 수가 있겠다. 예를 들어 분류 문제에서 LOOCV 에러율은 아래와 같이 구할 수 있다.

 여기서 $Err_{i}$ = I($y_{i}$ $noteq$ $\widehat{y}_{i}$) 이다. k-폴드 교차 검증의 에러율, 검증셋 에러율도 이걸 조금 고쳐서 정의할수가 있겠다.

 

그림 5.7 그림 2.13에서 본 이차원 분류 데이터를 로지스틱 회귀 모델로 학습한 결과. 보라색 점선이 베이즈 결정경계, 검은 선은 선형, 이차, 삼차, 사차로 추정한 로지스틱 회귀 결정 경계. 네 로지스틱 회귀 모델의 테스트 에러율은 각각 0.201, 0.197, 0.160, 0.162, 그리고 베이즈 에러율은 0.133 

 예를 들어 그림 2.13에서 봤던 2차원 분류 데이터를 학습하는 로지스틱회귀 모델을 사용한다고 하자. 그림 5.7의 왼쪽 위 판낼에서 검은색 선은 이 데이터를 로지스틱 회귀 모델로 학습시켜 구한 결정경계이다. 이 데이터는 시뮬레이션된 데이터이다보니 실제 테스트 에러율을 계산할수 있고, 구한 결과가 0.201인데, 베이즈 에러율인 0.133보다 크다.

 

 기본적인 로지스틱 회귀 모델은 베이즈 결정 경계만큼 유연성을 가지지 못해 비선형 결정 경계를 가질 수 있도록 입력 변수들의 다항식에 대한 함수로 확장을 해서 회귀를 하였는데, 3.3.2장에서 이전에 했었었다. 여기서 이차 로지스틱 회귀 모델을 만든다고 하면 아래와 같이 구할수가 있다.

 그림 5.7 오른쪾 위 판낼에서는 곡선의 결정 경계가 나오고 있는데 이전보다 테스트 에러율이 0.197로 약간만 증가하였다. 그림 5.7 아래 왼쪽 판낼을 보면 입력 변수에 대한 삼차적 곡선으로 로지스틱 회귀 모델을 학습하다보니 결과가 더 개선되었고, 테스트 에러율이 0.160으로 더 줄어들었다. 하지만 오른쪽 아래의 4차 다항식으로 확장시킨 경우 테스트 에러율이 약간 증가하고 말았다.

 

 현실에서는 실제가지고 있는 데이터로는 베이즈 결정 경계와 실제 테스트 에러율을 알 수가 없다. 그러면 그림 5.7에서 본 4가지 로지스틱 회귀 모델들 중에서 어떤걸 골라야 할까? 여기서 교차 검증을 사용하면 된다.

 

 

그림 5.8 그림 5.7에서 본 2차원 분류 데이터의 테스트 에러(갈색), 훈련 에러(파랑), 10-폴드 교차검증 에러(검정). 왼쪽 : 입력 변수의 차수에 대한 함수를 사용한 로지스틱 회귀. 다항 차수는 x축에 표기됨. 우측 : 여러 K값을 사용한 KNN분류기.

 

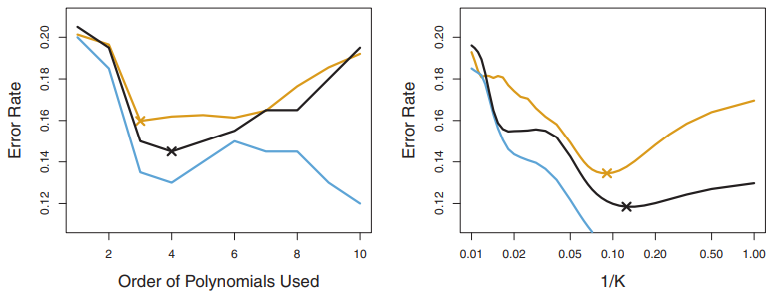
 그림 5.8의 왼쪽 판낼을 보면 검은색은 10-폴드 교차검증 에러율이고, 실제 테스트 에러율은 갈색, 훈련 에러율은 파란색이다. 이전에 봤다 시피 훈련 에러율은 유연성이 증가할수록 감소하는 경향을 보인다.(그림에서 볼수있다시피 테스트 에러율은 단조롭게 쭉 감소하지는 않지만 전체적으로 모델 복잡도가 증가할수록 감소하는 경향이 있다.)

 

 이와 반대로 테스트 에러율은 U자 형태를 보이는데, 10-폴드 교차검증 에러율은 실제 테스트 에러율을 잘 근사하고 있는것을 볼 수 있다. 테스트 에러율을 약간 과소추정을 하고 있지만, 실제 테스트 에러의 경우 4차 다항식일때 최소가 되고, 교차 검증으로 구한 결과 3차 다항식을 사용한 경우 최소가 되며 실제 테스트 커브의 최소 지점과 상당히 가까운걸 알수 있겠다.

 

 그림 5.8의 오른쪽 판낼에는 KNN 분류기를 사용한 경우의 3가지 커브를 보여주고 있다. 여기서 x축은 K를 사용했는데 CV 폴드 갯수 대신 최근접 이웃의 개수가 되겠다. 훈련 에러율은 복잡도/유연성이 증가할수록 감소하고 있으며, 훈련 에러율을 가지고 최적의 K를 찾는데 도움이 안된다고 볼수 있겠따. 교차 검증 에러 곡선의 경우 실제 테스트 에러를 과소 추정을 하고 있지만, 실제 최적의 K에 매우 가까운것을 알 수 있다.

 

 

 

 

5.2 부트스트랩 Bootstrap

 

 부트스트랩 Boostrap은 널리 사용되며 아주 효과적인 통계적 방법으로 사용하려는 통계적 학습 기법의 추정량이 얼마나 불확실한지 uncertainty를 측정하는데 사용할 수 있다. 간단한 예를 들자면 부트스트랩은 선형 회귀 모델의 계수 표준 오차를 추정하는데 사용할 수 있는데,  R 같은 통계 소프트웨어로 표준 오차같은 것들은 자동적으로 계산해주다보니 선형 회귀 모델에 대해서 이렇게는 잘 사용하지는 않지만, 부트스트랩의 강점은 통계 소프트웨어로 자동으로 계산할수 있는 출력이 아니거나 변동성을 구하기 힘든 경우를 포함하여 다양한 통계적 학습 기법에서 널리 쉽게 사용할수 있다는 점이다.

 

 이번 장에서는 간단한 모델로 어떻게 최적의 투자를 할지 결정하는 간단한 예시에서 부트스트랩을 사용하여 보자. 5.3장에서는 선형 회귀 모델의 회귀 계수들의 변동성을 평가하기 위해 부트스트랩을 사용하겠다.

 

 일단 고정된 소지금을 수익을 내는 두 금융 자산 X, Y에 투자한다고 하자. 여기서 X, Y은 양적 변수이다. 그리고 총 금액에 X에 투자한 비율을 $\alpha$, Y에 투자한 비율을 1 - $\alpha$라고 한다. 두 자산의 수익 사이에는 변동성이 존재하므로 투자에 전체 리스크, 분산을 최소화 하는 $\alpha$를 구하고자 한다.

 

 다시 말하면 Var($\alpha$ X + (1 - $\alpha$) Y)를 최소화 하고자 하는것이며, 이 리스크를 최소화 하는 $\alpha$를 아래와 같이 정의할수 있다. $\sigma^{2}_{X}$ = Var(X), $\sigma^{2}_{Y}$ = Var(Y),  $\sigma_{XY}$ = Cov(X, Y).

 

 실제 $\sigma^{2}_{X}$, $\sigma^{2}_{Y}$, $\sigma_{YX}$에 대한 값은 알 수 없으므로, 이 세 값에 대한 추정치인 $\widehat{\sigma}^{2}_{X}$, $\widehat{\sigma}^{2}_{Y}$, $\widehat{\sigma}_{XY}$를 이전의 X, Y에 대한 데이터들로 계산 하여야 한다. 그러면 아래의 식으로 투자 변동성을 최소화 시키는 $\alpha$ 추정량을 아래와 같이 구할수 있겠다.

 

 

그림 5.9 각 판낼들은 X, Y 투자에 대한 100개 수익 데이터들을 보여줌. 왼쪽 위 부터 오른쪾 아래까지 알파값 추정량은 0.576, 0.532, 0.657, 0.651

 그림 5.9은 시뮬레이션 데이터로 $\alpha$를 추정하는 과정을 보여주는데, 각 판낼에는 X, Y에 투자시 수익에 대한 100개의 데이터로 $\sigma^{2}_{X}$, $\sigma^{2}_{Y}$,  $\sigma_{XY}$에 대한 추정량을 식 (5.7)에 대입하여 $\alpha$의 추정치를 구하였다. 각 시뮬레이션된 데이터셋으로 추정한 $\widehat^{\alpha}$는 0.532 ~ 0.657가 되겠다.

 

 그러면 여기서 $\alpha\ 추정량이 얼마나 정확한지 측정하고 싶을텐데, $\widehat{\alpha}$의 표준 편차를 추정하기 위해서는 X, Y 쌍 100개 가지고 $\alpha$의 추정량을 계산하는 과정을 1000번 반복하면 된다. 그렇게 $\alpha$ 추정량 1000개 $\widehat{\alpha}_{1}$, . . . , $\widehat{\alpha}_{1000}$을 구하면 된다.

 

왼쪽 : 모 집단 true population으로부터 생성시킨 1000개의 시뮬레이션 데이터셋으로 추정한 알파값들의 히스토그램, 중앙 : 하나의 데이터셋으로부터 1000개의 부트스트랩 샘플들을 구하여 추정한 알파값들의 히스토그램, 우측 : 왼쪽과 중앙의 알파값 추정량에 대한 박스 플롯. 각 판낼에서 분홍색인 실제 알파값을 나타내고 있다.

 그림 5.10의 왼쪽 판낼은 각 추정치의 히스토그램을 보여주고 있다. 여기서 사용한 시뮬레이션의 파라미터들은$\sigma^{2}_{X}$ = 1, $\sigma^{2}_{Y}$ = 1.25,  $\sigma_{XY}$ = 0.5로 설정되어 있고, 실제 $\alpha$값은 0.6이다. 이 실제 알파값은 히스토그램에서 수직선으로 표시해 두었다. $\alpha$ 추정량 1000개의 평균을 구한 결과는 아래와 같으며 실제 $\alpha$ = 0.6에 가까운 결과를 얻을수가 있다.

 그리고, 이 추정량의 표준편차는 아래와 같으며 $\widehat{\alpha}$ : SE($\widehat{\alpha}$) $\approx$ 0.083으로 꽤 정확한 결과를 얻었다고 볼수 있겠다.

  

 정리하자면 모 집단으로 구한 샘플들로 추정한 결과 $\widehat{\alpha}$와 $\alpha$의 차이가 평균적으로 0.08정도 밖에 되지않는다고 볼수있다.

 

 하지만 현실에서는 모집단으로부터 새 샘플들 그러니까 실제 데이터를 구할수 없다보니 위 SE($widehat{\alpha}$)를 추정하는 과정을 사용할 수 없다. 하지만 부트스트랩 방법을 이용해서 새로운 샘플 셋을 얻는 과정을 모방해서 계산할수가 있고, 별도로 샘플들을 생성하는 과정 없이 $\widehat{\alpha}$의 변동을 추정할수가 있다.

 

정리

-> 위 내용은 추정량의 불확실한 정도를 표준 편차로 계산하는 과정을 정리함

-> 모집단, 파라미터를 알고 있어 데이터를 생성하여 표준 편차, 불확실성을 계산할 수 있었슴.

-> 하지만 현실에서는 모집단을 모르는 경우가 많으며, 표준편차, 불확실성을 계산할수가 없음

=> 부트스트랩으로 여러 셋을 생성하고, 각 셋들의 추정량들의 평균으로 표준편차, 불확실성을 계산한다.

 

 

부트스트랩이란

 부트스트랩은 모집단으로부터 독립적인 데이터셋을 여러번 구하는게 아니라 원본 데이터셋에서 여러번 데이터를 샘플링을 해서 서로 다른 데이터셋들을 얻는 방법이다.

 

그림 5.11 데이터 3개뿐인 데이터셋가지고 부트스트랩 방법을 사용하는 예시. 각 부트스트랩 데이터셋은 데이터가 3개이며, 원본 데이터셋으로부터 샘플을 뽑아 만들었다. 각 부트스트랩 데이터셋은 알파 추정값을 구하는데 사용된다.

 

 이후에도 추가적인 내용이 있으나 부트스트랩에 대해서는 여기까지