4.5 분류 방법들의 비교 A Comparison of Classification methods
이번 장에서는 우리는 3가지 분류 방법인 로지스틱 회귀, LDA, QDA까지 살펴봤습니다. 2장에서도 KNN에 대해서 이야기 해썼는데, 몇 가지 상황에서 이런 방법들이 성능이 어떻게 나오는지 한번 살펴봅시다.
이 방법들끼리 고안된 배경은 다르지만 로지스틱회귀와 LDA 방법들은 아주 가까이 관련되어 있어요. 두 클래스를 분류하는 상황에서 입력변수 p = 1이라고 할께요. 그러면 $p_{1}$(x), $p_{2}$ = 1 - $p_{1}$(x)가 관측치 X = x가 주어질때 클래스 1 혹은 클래스 2에 속할 확률이 될거에요. LDA의 경우 식 (4.12), (4.13)을 로그 오즈를 취하면 아래와 같이 될겁니다. $c_{0}$, $c_{1}$은 $\mu_{1}$, $\mu_{2}$, $\sigma^{2}$에 대한 함수가 되겠습니다.
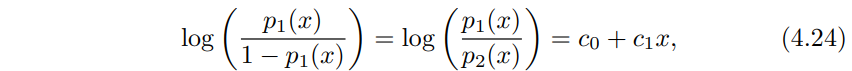
식 (4.4)로부터 로지스틱 회귀의 경우 아래와 같이 정리할 수 있는데

식 (4.24)와 식(4.25)둘다 x에 대한 선형 함수에요. 그래서 로지스틱 회귀와 LDA는 선형 결정 경계를 만들어 냅니다. 두 방법사이 차이점이라 하면 $\beta_{0}$, $\beta_{1}$는 최대 가능도법 maximum likelihood로 구한다는것이고, $c_{0}$, $c_{1}$는 정규 분포를 따르는 평균과 분산 추정량으로 계산한다는 점입니다. LDA와 로지스틱 회귀 사이 이런 관계가 p > 1인 다차원 데이터에서도 존재해요.
로지스틱 회귀와 LDA의 차이점이 학습하는 과정뿐이다보니 두 방법은 비슷한 결과를 보이고 있어요. 하지만 항상그렇지는 않습니다. LDA는 관측치들이 각 클래스들끼리 공통된 공분산을 가지는 가우시안 분포를 따른다고 가정하고 있어, 이 가정이 올바른 경우 로지스틱 회귀를 능가합니다. 역으로 로지스틱 회귀난 가우시안 가정이 적합하지 않은 경우 LDA보다 더 좋으성능을 보입니다.
2장에서 봤던 KNN은 이번장에서 본 분류기랑은 완전히 다른 방법인데, X = x에 대한 관측치를 예측하기 위해서, x와 가까운 K개의 관측치를 찾아야 합니다. 그리고 주위에 있는 관측치가 많이 속해있는 클래스로 분류되요. 그래서 KNN은 완어떠한 결정 경계의 형태를 가진다는 가정이 없는 완전히 비모수적인 방법이라고 할수 있습니다.
그러므로 이 방법은 LDA나 로지스틱회귀보다 결정 경계가 완전히 비선형적인경우 더 뛰어난 성능을 보인다고 할 수 있어요. 하지만 KNN은 입력 변수들이 얼마나 중요한지 알려주는게 없다보니 표 4.3과같은 계수에 대한 테이블을 만들수가 없습니다.
마지막으로 QDA는 비모수적 방법인 KNN과 선형 LDA, 로지스틱 회귀 방법들을 절충한거라고 할수 있어요. QDA는 이차 결정 경계를 가정하다보니, 선형 방법들보다 더 넓은 범위를 정확한 모델을 만들수가 있어요. 하지만 KNN만큼 유연하지는 않고, QDA는 결정 경계의 형태에 대한 가정들을 만들다 보니 데이터가 많이 있을수록 더 좋은 성능을 보여요.
이 네가지 분류 방법의 성능을 보기위해서 6가지 서로 다른 시나리오의 데이터를 생성하였습니다. 세가지 시나리오 에서는 베이즈 결정경계는 선형적이고, 나머지 시나리오에서는 비선형적이라고 하겠습니다. 각 시나리오는 훈련데이터가 100개라고 해요. 그리고 이 데이터셋들로 학습을하고, 테스트 에러율을 구해볼게요.


그림 4.10가 선형 시나리오에 대한 결과, 그림 4.11은 비선형적인 시나리오들의 테스트 에러율의 결과를 보여주고 있습니다. KNN은 K를 지정하는게 필요하니 K는 1로 지정한 경우와 5장에서 다룰 교차검증 cross validation이란 방법으로 자동적으로 찾은 K를 사용하였습니다.
이 6개의 시나리오들은 p = 2이며, 아래와 같습니다.
- 시나리오 1 : 클래스 2개에 각각 20개의 관측치가 있고, 한 클래스에 속하는 관측치들ㅈ은 서로 다른 클래스와 상관관계를 가지고 있지 않아요. 그림 4.10의 왼쪽 그림에서 LDA가 잘동작하고 있지만 KNN는 편향을 제거하여 분산이 오프셋되지않다보니 나쁜 성능을 보이고 있습니다. QDA또한 LDA보다 필요 이상으로 유연하다보니 좋은 성능이 나오지않아요. 로지스틱 회귀는 선형 결정 경계를 가정으로 하고있어 LDA보다 성능이 약간 떨어지는걸 볼수 있습니다.
- 시나리오 2 : 자세한 사항은 시나리오 1과 동일하지만 두 입력변수간에 -0.5의 상관관계를 가진다고 할께요. 그림 4.10의 중간 판낼을 보면 이전 시나리오와 비교하면 각 방법들의 성능이 약간 바뀐걸 볼수 있어요.
- 시나리오 3 : $X_{1}$과 $X_{2}$는 t분포로를 따르며, 각 클래스 당 관측치가 50개를 가져요. t 분포는 정규 분포와 비슷한 형태이지만 평균으로부터 더 멀어진 경향을 보여요. 여기서도 결정경계는 선형적이고, 로지스틱을 학습한다고 할께요. 하지만 LDA의 가정을 위반해서, 다시말하면 정규분포를 따르지않아 그림 4.10의 오른쪽 판낼에서 로지스틱이 LDA보다 더 좋은 성능을 보이고 있고, 다른 방법들보다 우수한 성능을보여요. 하지만 비정규성을 따르다보니 QDA의 성능이 상당히 떨어졌어요.
- 시나리오 4 : 데이터를 정규 분포로 생성했고 첫번쨰 클래스의 입력변수들은 0.5의 상관관계를 가지고 있고, 두번쨰 클래스의 입력 변수들은 -0.5의 상관관계를 갖는다고 할꼐요. 이 상황은 QDA의 가정을 잘 따르므로 이차 결정 경계의 형태가 나오죠. 그림 4.11의 왼쪽 패널은 QDA가 다른 방법들에 비해 큰 성능을 보이는걸 알 수 있어요.
- 시나리오 5 : 각 클래스들에 대한 관측치들은 정규분포로 생성했으며, 입력 변수 끼리 상관관계를 가지고 있지 않습니다. 하지만 반응 변수들을 $X_{1}^{2}$, $X_{2}^{2}$, $X_{1}$ x $X_{2}$를 입력변수로 하는 로지스틱 함수로부터 얻었다고 할께요. 그결과 결정 경계가 이차적으로 되다보니 그림 4.11의 중간 판낼에서 QDA가 최고의 성능을 보이고 KNN_CV가 뒤쫓아오고 있어요. 하지만 선형 방법들은 성능이 크게 떨어집니다.
- 시나리오 6 : 이전 시나리오와 동일하나 반응 값들을 더 복잡한 비선형 함수로 얻은 경우로, 결과를 보면 QDA의 이차 결정 경계는 이 데이터를 적절하게 모델링하지 못하고 있습니다. 그림 4.11의 오른쪽 판낼을 보면 QDA는 다른 선형 모델보다 약간 더 나은 성능을 보이기는 하지만 가장 유연한 KNN-CV방법이 최고의 결과를 보이고 있어요. 이 시나리오에서는 데이터가 너무 복잡한 비선형 관계를 가질때 유연성의 정도(K값)을 적절하게 지정하지 않으면 KNN같은 비모수적 방법도 여전히 성능이 뒤떨어지는걸 볼 수 있어요.
이 여섯가지 예시들을보면 모든 상황에서 최고의 성능을보이는 한가지 방법은 존재하지 않습니다. 실제 결정경계가 선형인 경우 LDA와 로지스틱 회귀가 잘 동작하는 편이었으며, 결정경계가 약간 비선형적이라면 QDA가 좋은 성능을 보였어요. 마지막에 아주 복잡한 결정 경계를 갖는 경우 KNN같은 비모수적 방법이 가장 뛰어났습니다. 하지만 비모수적 방법의 완만도(K값)을 신중하게 정해야해요. 다음 장에서는 올바른 완만도를 찾기위한 수많은 방법들을 살펴보고 최적의 방법을 골라보겠습니다.
마지막으로 3장에서 배운 내용을 다시 생각해보면, 입력 변수들을 변환을 하고 회귀를 수행해서 입력과 반응 사이 비선형적인 관계를 다룰수가 있었습니다. 비슷하게 분류에서도 그렇게 할수가 있어요. 예를들면 $X^{2}$, $X^{3}$, $X^{4}$같은 입력변수들을 추가해서 로지스틱 회귀의 유연한 버전을 만들수도 있겠습니다.
하지만 이거는 분산이 크게 증가하느냐에 따라 성능이 개선될수도 있고 안될수도 있어요. 이건 추가된 유연성이 편향을 충분히 크게 상쉐시킬지에 달렸거든요. LDA에서도 똑같이 적용할수 있겠습니다. 만약 LDA다가 이차항이나 교차항을 추가시키면, 계수 추정치가 다르더라도 QDA랑 똑같은 형태가 될수도 있을거에요. 이러한 방법들로 LDA를 QDA로, QDA를 LDA로 변화시킬수 있겠습니다.
5. 리샘플링 기법
리샘플링 기법은 현대 통계학에서 필수적인 도구입니다. 이 방법은 훈련 데이터셋으로 반복해서 샘플을 뽑고, 이렇게 뽑은 샘플로 모델을 학습시켜 전체 훈련 데이터셋을 한번에 학습시킨것과 다른 모델을 만들어 추가적인 정보를 얻을수가 있어요. 예를든다면 선형 회귀 모델의 변동성을 추정하고자 할때 훈련 데이터셋으로부터 다른 샘플들을 반복해서 뽑고 이걸 학습을 시키면, 다른 학습 모델을 만들어 추가적인 정보를 얻을수가 있습니다. 이러한 방법을 덕분에 기존 원본 훈련 데이터 샘플을 만든 모델과는 다른 정보들을 얻을수 있게 됩니다.
리샘플링 기법은 계산 비용이 꽤 클수 있는데, 훈련 데이터에서 여러 하부집합들을 뽑아 여러번 통계적인 학습을 수행할수도 있거든요. 하지만 최근 계산 성능이 좋아지면서 리샘플링 기법의 계산 비용 문제는 사라졌습니다. 이번 장에서는 가장 널리 사용되는 리샘플링 기법인 교차 검증 cross validation과 부트스트랩 boostrap 기법에 대해서 이야기 해봅시다.
이 방법 둘다 많은 통계적 학습 과정에서 매우 자주 사용되는 방법인데, 예를들어 교차 검증 같은 경우에는 우리가 만든 통계적 학습 모델의 테스트 에러율을 구하여, 모델의 성능을 보거나 적절한 유연성 정도를 찾기위해서 사용해요. 이렇게 추정한 모델의 성능을 평가하는 과정을 모델 평가 model assessment라고 부르고, 모델의 유연성 정도를 찾아내는 과ㅏ정을 모델 선택 model selection이라고 부릅니다. 부트스트랩 boostrap은 다양한 상황에서 사용되고 있는데, 가장 흔하게는 주어진 통계적 학습 방법의 파라미터 추정치가 얼마나 정확한지 측정하고자 사용되요.
5.1 교차 검증 cross-validation
2장에서 테스트 에러율 test error rate와 훈련 에러율 train error rate의 차이를 살펴봤었습니다. 테스트 에러율은 학습하지 못한 관측치를 예측할때 평균 에러율이었었어요. 데이터셋이 주어지고 테스트 에러가 낮은 통계적 학습 방법이 사용되어요. 테스트 에러는 테스트 데이터셋이 있으면 쉽게 계산할수 있지만 가끔 없는 경우도 존재합니다.
반대로 훈련 에러는 통계적 학습 모델에다가 훈련떄 사용한 관측치들을 넣어 쉽게 계산할 수 있어요. 하지만 2장에서 봤다 시피 훈련 에러율은 테스트 에러율과 꽤 다를수 있으며, 대체로 훈련 에러율은 테스트 에러율보다 크게 떨어져요.
테스트 에러율을 계산하는데 필요한 테스트 데이터셋이 없을때 가지고 있는 데이터로 이 척도를 구하는 많은 방법들이 있는데, 어떤 방법들은 훈련 에러율을 수학적인 방법으로 조정해서 테스트 에러율을 구하기도 하지만 이건 6장에서 살펴보겠습니다.
이번 장에서는 학습 과정에서 사용될수 있는 훈련 관측치들의 일부를 홀드 아웃hold out/집어와서 테스트 에러율을 계산하는 방법들을 이야기해보고, 통계적 학습 기법들에 적용해봅시다.
5.1.1 ~ 5.1.4장에서는 양적 반응을 가지는 회귀 모델을 가정하고 간단하게 살펴보고, 5.1.5장에서는 질적 변수를 다루는 분류 문제를 살펴봅시다. 질적 변수든 양적 변수든 키 컨샙은 같다고 보면 되요.
5.1.1 검증 데이터셋 방법 The Validation Set Approach

한번 우리가 훈련 에러율을 구하고 싶을대, 그림 5.1의 검증 데이터셋 방법이 사용될 수 있는대 매우 간단한 방법이에요. 그냥 주어진 데이터셋을 훈련데이터셋 training set과 검증 데이터셋 validation set/ 홀드아웃데이터셋 hold-out set으로 임의로 나눠주기만 하면 되거든요. 그러면 모델은 훈련 데이터셋을 학습하고, 학습한 모델을 검증 데이터셋으로 결과를 예측해서 검증하면 되요. 그렇게 양적 반응에 대한 MSE를 계산해서 검증 데이터셋의 에러율을 구하면 그게 테스트 에러율로 보면 되겠습니다.
한번 이 검증 데이터 셋 방법을 차량 데이터셋에다가 사용해볼꼐요. 우리는 지난 3장에서 mpg와 마력 사이에 비선형 관계가 있는걸 봤었어요. 그리고 마력과 $마력^{2}$으로 mpg를 예측하는 모델을 만들어서 선형 항만 있었을때보다는 더 나은 결과를 얻을수가 있었습니다. 그렇다보니 무조건 더 높은 차수를 가지고 있으면 더 좋은 결과를 얻을수 있을까? 궁금할수 있을거에요.
3장에서 이 질문에 대해서 2차항과 더 고차 항을 사용하는 선형 회귀의 p value를 보면서 확인할수 ㅇ있었습니다. 하지만 p value말고도 검증 데이터셋을 사용해서 확인할 수도 있어요. 그러면 한번 392개의 관측치들을 196개의 훈련 데이터셋과 196개의 검증 데이터셋으로 분할시켜볼꼐요.
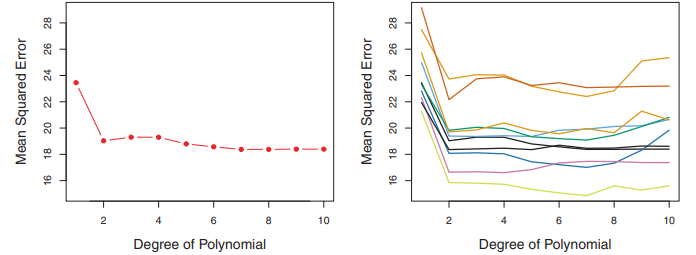
검증 데이터셋 에러율은 훈련 데이터셋으로 여러가지 복잡도/차수를 가진 모델들을 학습하고, 검증 셋으로 성능 평가해서 구할수가 있겠죠. 여기서 MSE를 검증 셋의 에러 평가 척도로 사용해서 보았고, 그 결과를 그림 5.2의 왼쪽 판낼에서 볼수 있어요.
이차 학습 모델의 검증 데이터셋 MSE는 선형적인 모델보다 상당히 줄어들었지만, 삼차항 모델같은 경우 이차 모델보다 약간 증가하였죠. 그래서 회귀 모델에서 삼차항까지 포함시킨다고해서 간단하게 이차항을 썻을때보다 예측성능이 더나아진다고 볼수는 어렵습니다.
한번 그림 5.2의 판낼처럼 만들기위해서 한번 데이터셋을 훈련 데이터셋과 검증 데이터셋으로 임의로 나눴다고 해볼깨요. 그런데 이 동작을 여러번 반복하면, 테스트 MSE도 계속 다르게 나올거에요. 이 내용이 그림 5.2의 오른쪽 판낼에서 나오는대 서로 다른 10개의 훈련데이터로 학습하고, 검증데이터셋으로 평가한 테스트 MSE를 보여주고 있어요.
모든 곡선들을 보면 이차항 까지만 포함된 모델의 경우 선형 항만 포함된 모델보다 훨씬 테스트 MSE가 적은걸 볼수 있어요. 그러므로 10가지 경우들을 보면서 3차항이나 더 고차항을 쓴다고해서 더 나은 성능을 얻을수 있지 않다는걸 알 수 있어요. 그리고 서로 다른 회귀 모델가지고 테스트 MSE를 구했으니 서로 다른 곡선들이 나오는게 당연하구요. 그렇다보니 한 모델이 가장 낮은 검증 MSE를 가진다고 하기도 힘들어요. 이런 곡선들의 변동성을 고려해서 우리가 결론 내릴수 있는건 이 데이터셋에 선형 모델이 적합하지 않다는 거구요.
검증 데이터셋 방법은 간단하며 구현하기도 쉽습니다. 하지만 다음의 두가지 결점을 가지고 있어요.
1. 그림 5.2에 보시다시피, 검증 에러율은 훈련 데이터셋과 검증 데이터셋이 임의로 만들어지는거에 크게 영향을 받아 변동이 심합니다.
2. 검증 데이터셋방법은 전체 관측치의 일부를 사용하다보니, 검증 데이터셋은 훈련 데이터셋보다 적어요. 그리고 적은 데이터로 훈련하면 성능이 떨어지다보니, 검증 데이터셋 에러율은 전체 데이터셋으로 학습한 모델의 테스트 에러율을 과소평가/ 전체 데이터셋을 학습한 모델의 테스트 에러율보다 떨어지는 경향이 있어요.
그래서 다음 장에서는 검증 데이터셋 방법이 가지고 있는 두가지 문제를 개선하고자 나온 방법인 교차 검증 cross validation에 대해서 알아봅시다.
'번역 > 통계적학습법개론' 카테고리의 다른 글
| [통계기반학습개론] 5.1.4 K 폴드 교차검증의 편향-분산 트레이드 오프 ~ 5.2 부트스트랩 (0) | 2021.03.02 |
|---|---|
| [통계기반학습개론] 5.1.2 LOOCV 하나만 가지고 교차검증, 5.1.3 K-폴드 교차 검증 (0) | 2021.03.01 |
| [통계기반학습개론] 4.3.4 다중 로지스틱 회귀와 선형/이차 판별 분석 (0) | 2021.02.21 |
| [통계기반학습개론] 4. 분류 Classification 와 로지스틱회귀모델 (0) | 2021.02.19 |
| [통계기반학습개론] 3.4 마케팅 전략/3.5 KNN과 선형 회귀 모델 비교 (0) | 2021.02.06 |