4. 분류 Classification
지난 3장에서는 선형 회귀 모델에 대해서 이야기 하였습니다. 회귀 모델에서 반응 변수 Y는 양적 변수였었죠. 하지만 반응 변수가 질적 변수인 경우도 많이 있어요. 예를들면 눈의 색깔도 질적 변수로 파란색, 갈색, 녹색같은게 있겠죠. 종종 이런 질적 변수 qualitative variaables를 카테고리 categorical이라고 부르기도 해요. 그리서 이런 용어들을 자주 사용할거고 이번 장에서는 질적 반응, 카테고리를 예측하는 방법들 즉 분류 기법에 대해서 배워봅시다.
주어진 데이터, 관측된 데이터, 입력 데이터 x를 가지고 질적 반응 변수, 카테고리를 예측하는일을 분류 라고 부릅니다. 왜냐면 주어진 데이터를 가지고 이게 어느 카테고리 혹은 클래스에 속하는지를 다루거든요. 하지만 분류를 하기 위해서 우선은 어디에 속하는지 판단하기 위해서 각 카테고리별 확률을 예측하여 봅시다. 그러면 이건 회귀적인 방법을 사용한다고 볼수 있겠죠.
질적 반응을 예측하는데 사용가능한 아주 많은 분류 기법들, 분류기들이 있는데 우선 2.1.5, 2.2.3장에서 몇가지를 살펴보려고 합니다. 이번 장에서 가장 널리 사용되는 분류기인 로지스틱 회귀 logistic regression과 선형 판별 분석 linear discriminant anlaysis 그리고 최근접 이웃 K-nearest neighbor에 대해서 이야기해봅시다. 그리고 차후 챕터에서 일반화 가산 모델 generalized additive models(7장), 트리 모델, 랜덤 포레스트, 부스팅(8장), 서포트벡터 머신(9장)과 같이 더 복잡한 방법들을 이야기해봐요.
4.1 분류 개요 An Overview of Classification
분류 문제는 어떻게 보면 회귀 문제보다 더 많이 존재한다고 할수 있을거 같아요. 예를들자면
1. 어떤 사람이 병증 때문에 응급실에 왔습니다. 3가지 의료 상태 중 하나를 줄 수 있겠는데, 예를 들면 (정상, 긴급, 사망) 같은 경우가 있다고 해요. 각자 사람의 증상/상황을 보고 어떻게 분류하여야 할까요?
2. 온라인 은행 서비스같은 경우 사용자의 주소, 이전 거래 기록, 그 이외의 정보로 현재 거래가 사기(위법)인지 아닌지 판단할수 있어야 해요.
3. 어떤 질병이 있는 혹은 없는 사람들의 DNA 시퀀스 데이터가 있다고 합시다. 그러면 생명공학자는 이 질병을 야기시키는/원인이 되는 DNA변종이 있는지 다시 말하면 이 사람이 병에 걸릴 위험이 있는지 없는지 판단할 수 있어야 해요.
회귀 상황과 마찬가지로 분류 상황에서도 훈련 데이터/관측치 observations ($x_{1}$, $y_{1}$), . . .($x_{n}$, $y_{n}$)을 가지고 있고, 이 데이터를 사용해서 분류기를 만들수가 있어요. 그리고 우리가 만든 분류기가 훈련 데이터에만 잘 동작하는게 아니라 (훈련 과정에 사용하지 않은)테스트 관측치/테스트 데이터에서도 잘 동작되야하겠죠.

이번 장에서는 시뮬레이션으로 만든 채무 불이행/디폴트에 관한 데이터셋을 사용하여 분류의 개념에 대해서 볼것이고, 사람들의 연간 수입과 매달 신용카드 대금 balance 등을 보고 신용카드 지출 채무 불이행 여부를 예측해봅시다. 이 데이터는 그림 4.1에서 볼수 있어요. 이 그림는 1만명의 연간 수입 income과 매달 신용카드 대금 일부를 그래프로 띄웠습니다.
그림 4.1의 왼쪽 판낼에서 채무 불이행한 사람들은 주황색, 그렇지 않은 사람은 파랑색으로 나타내고 있으며 (전반적인 체무 불이행 비율은 3%정도 됩니다.) 카드 대금이 클수록 채무 불이행이 큰것으로 나오고 있습니다. 그림 4.1의 오른쪽 판낼에서는 두 박스 플롯을 보여주고 있습니다. 첫번째 박스 플롯은 채무 불이행 여부에 따른 카드 대금 분포를, 두번째 그림에서는 채무 불이행에 따른 수입의 분포를 보여주고 있습니다.
이번 장에서는 카드 대금 $X_{1}$과 수입 $X_{2}$로 채무 불이행 여부 Y를 예측하는 모델을 만드는 방법을 배워보도록 합시다. Y는 양적 변수가 아니므로 3장에서 본 단순 선형 회귀 모델은 사용할수가 없어요.
그림 4.1에서는 입력 변수 카드 대금 balance과 반응 변수 채무 불이행 defualt이 중요한 관계를 가지고 있는걸 볼수 있겠습니다. 대부분의 현실 세계에서는 입력 변수와 반응 변수 사이에 이렇게 강한 관계를 가지고 있지는 않습니다. 하지만 이번 장에서 분류 과정을 쉽게 이야기하기위해서 입력과 반응 사이의 관계가 과장될 정도로 강한 예시를 사용해서 보겠습니다.
4.2 왜 선형 회귀가 아닐까요? Why Not Linear Regression?
반응 변수가 질적 변수인 경우 선형회귀가 적절하지 않다고 했는데 왜그럴까요? 한번 응급실에 온 환자의 증상을 보고 상태가 어떤지 진단을 해본다고 합시다. 진단 결과 다음 3가지 경우가 있다고 해요. 뇌졸증 stroke, 약물 과다복용 drug overdose, 간질 발작 epileptic seizure. 이 값들을 아래와 같이 반응 변수 Y로 인코딩을 해봅시다.

이렇게 인코딩을 하고, 최소 제곱법을 사용해서 입력 변수의 속성들 $X_{1}$, ..., $X_{p}$로 Y를 예측할 수 있도록 선형 회귀 모델을 학습해 봅시다. 하지만 이 인코딩 방식 처럼 뇌졸증 stroke와 간질 발작 epileptic seizure 사이에 약물 과다 복용 drug overdose를 넣어버리면 출력 값 사이에는 순서가 있는것이 되며, (뇌졸증 - 약물 과다복용) == (약물 과다복용 - 간질 발작) 다시 말하면 뇌졸증과 약물과다복용의 차이와 약물 과다복용과 간질 발작의 차이가 같다고 할수 있겠죠. 하지만 진단 결과들 끼리는 순서가 존재하지도 않고 2- 1 == 3 - 2가되는 관계 같은건 존재하지도 않아요.
세가지 상태 끼리 완전히 다른 관계를 가지고 있다고 본다면 그러니까 순서를 가진게 아닌 카테고리로 본다면 옳은 인코딩 방식이라고 할 수 있을거에요.

그리고 이 인코딩 각각으로 완전히 다른 선형 회귀 모델들을 만들어 테스트 입력이 주어질때 여러개의 예측값(stroke에 대한 예측, drug overdose에 대한 예측, epileptic seizure에 대한 예측)값들이 만들어 지겠죠.
만약 반응 변수 값들이 순한 mild, 중간 moderate, 센 severe처럼 순서를 가지고 있다고 보는게 자연수러운 경우에는 1, 2, 3으로 인코딩시키는게 유용할 거에요. 하지만 경우의 수가 3개 이상인 정적 반응 변수를 자연스럽게 선형 회귀 모델에서 사용가능한 양적 변수로 바꿀 방법이 없어요.
이진 양적 반응 binary qualtative response(반응 변수 값이 2개인 경우)의 경우는 간단한데, 예를들면 환자 상태가 뇌졸증 혹은 약물 과다복용 두가지 경우에 대한 확률만 있다고 할게요. 그러면 이걸 3.3.1장에서본 가변수를 사용해서 반응 변수를 아래와 같이 인코딩할수 있을거에요.

이렇게 되면 이진 반응을 선형 회귀 모델로 학습시키고, $\hat{Y}$ > 0.5이면 약물 과다복용을 아니면 뇌졸증으로 예측할 수 있을거에요. 이진 분류 문제에서는 위 인코딩을 뒤집더라도 선형 회귀 모델은 같은 예측 결과를 나오니 어렵지는 않습니다.
위와 같이 반응 변수가 0/1로 인코딩 된 경우 최소제곱을 이용한 회귀 모델에서 잘 동작하는데, 예를 들면 X$\hat{\beta}$를 Pr(약물 과다복용 | X)을 추정하도록 선형 회귀로 얻은 모델이라고 할수 있을거에요.

하지만 선형 회귀를 사용한다면 그림 4.2같이 [0, 1]사이 구간 밖을 나갈수 있어 확률로 다루기는 힘들어요. 하지만 선형 회귀 모델의 예측 결과는 순차적이다 보니 처리되지 않은 확률 추정치 crude probability estimates라고 할수 있겠죠. 아무튼 이진 반응 결과를 예측하기 위해서 선형회귀를 사용하는 분류 방법을 LDA Linear Discriminant analysis라고 하는데 4.4장에서 살펴봅시다.
하지만 가변수 방법은 3개이상인 경우의 수로 확장해서 쓰기가 힘들어요. 이런 이유로 다음 장에서 나오는 방법이 이런 반응변수들을 다루는데 적합합니다.
=> 이 부분이 좀 햇갈리는데 아래와 같이 정리 할 수 있겠다.
경우의 수들을 1, 2, 3과 같이 인코딩 해버리면 결과 끼리 순서가 있는 것으로 만들어 버리는 문제가 있다.
* 라벨이 순서가 있는 경우는 괜찬으나 순서가 없는 경우는 문제가 된다.
가변수를 이용해여 0과 1로 인코딩 하는 경우 경우의 수가 2개일 때만 사용 가능하다.
4.3 로지스틱 회귀 Logistic Regression
디폴트 데이터셋을 생각해보면 디폴트 유무를 두 카테고리 Yes, No로 만들수 있을거에요. 하지만 Y를 직접 구하도록 모델링하기 보다는 로지스틱 회귀에서는 해당 카테고리에 속할 확률을 구하도록 모델링 합니다.
디폴트 데이터셋의 경우에는 로지스틱 회귀 모델은 디폴트될 확률을 구하겠죠. 예를들면 채무 잔액 밸런스 balance가 주어질때 디폴트가 될 확률은 아래와 같이 정리할수 있을거에요.

Pr(default = Yse | balance)의 값은 0, 1 사이가 될것이며 p(balance)로 축약할게요. 이 예측 값으로 디폴트 유무를 판단할수 있겠죠. 예를들어 어떤 사람이 p(balance) > 0.5이라면 이 사람은 default = Yes 라고 볼수 있겠습니다. 이걸 조금 더 수정하자면 회사가 디폴트 위험 여부를 보수적으로 판단한다면 하한 임계치를 0.1로 낮출수도 있을거에요.
4.3.1 로지스틱 모델
어떻게 p(X) = Pr(Y = 1 | X)와 X 사이 관계를 모델링 할 수 있을까요?(편의를 위해서 반응을 0과 1만 쓰겠습니다.) 4.2장에서 선형 회귀 모델을 사용해서 확률을 구할수 있다고 얘길 했었습니다.

우리가 카드 대금 balance로 default=Yes 인지 예측하기 위해서 이 방법을 사용한다면, 그림 4.2의 왼쪽 판낼 같은 모델이 만들어 질거에요. 이 그림을 보시면 이 방법의 문제가 나오는데 카드 대금이 0에 가까우면 디폴트일 확률 값이 -로 내려갑니다.. 카드 대금이 너무 크다면 1을 또 넘어갈거에요. 이런 예측 결과는 말도 안되고, 디폴트가 될 확률을 구해야하므로 카드 대금에 상관없이 0과 1사이에 속해야 합니다. 또, 이 문제는 신용 디폴트 데이터에서만 생기는게 아니구요.
하지만 아무리 직선 모델로 0/1인 반응 변수로 학습을 하던간에 p(X) < 0 또는 p (X) > 1이 되는 경우가 생길수 밖에 없습니다. 이 문제를 피하기 위해서 모든 X가 0과 1사이 값을 가지도록 하는 함수를 사용해서 p(X)를 모델링 해야 합니다. 많은 함수들이 있지만 이번에는 로지스틱 회귀를 다루므로 로지스틱 함수를 사용하겠습니다.
* 로지스틱 함수

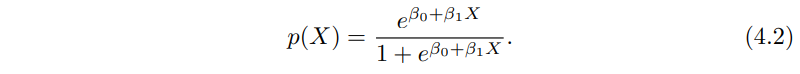
식 (4.2)의 로지스틱 회귀 모델을 학습하기 위해서는 다음장에서 설명할 최대 가능도법 maximum likelihood를 사용해야 합니다. 그림 4.2에서 로지스틱 회귀 모델을 디폴트 데이터에 학습 시킨 결과를 보여주고 있는데, 카드 대금이 적을수록 디폴트 확률이 0에 가까워지지만 0에는 안되고 있죠. 반대로 카드 대금이 클수록 1에 가까워지지 1이 되지는 않습니다.
로지스틱 함수는 항상 이런 S형태의 곡선을 만들며 X의 값에 상관없이 우리가 얻고자하는 확률 예측값을 얻을수가 있어요. 그리고 왼쪽 그림에서 이 로지스틱 회귀 모델이 선형 회귀 모델보다 확률 범위들을 더 잘 적합하고 있는걸 볼수 있어요. 두 모델로 구한 평균 확률은 0.0333으로 같으며, 이 데이터셋의 채무 불이행, 디폴트 한 사람의 비율과도 같아요.

식 (4.2)를 약간 변형하면 위와 같이 바꿀 수 있는데 이걸 오즈 odds라고 부르며 0 ~ 무한대 사이의 값을 가지고 있어요. 이 오즈가 0, 무한대에 가까울 수록 여기서 사용된 확률이 매우 낮거나 높다고 할수 있겠습니다. 예를 들어 평균적으로 5명중 1명이 디폴트가 된다고 하면 p(X) = 1/5 = 0.2가 되고, 0.2/(1-0.2) = 1/4, 오즈는 1/4가 됩니다. 10명 중 9명이 디폴트가 된다면 p(X) = 9/10이고 오즈는 0.9/(1 - 0.9) = 9가 될 거에요. 오즈는 확률이 작으면 작게, 크면 크게 하다보니 확률 대신에 자주 사용하고 있습니다.
위 (4.3) 양변에다가 로그를 취하면 다음의 식을 얻을수 있는데 왼쪽은 로그 오즈 log-odds 혹은 로짓 logit이라고 부르고 있어요. 결국 로지스틱 회귀 모델 (4.2)은 X에 대해 선형함수인 로짓을 가지고 있습니다.

3장에서 선형 회귀 모델을 다룰때 $\beta_{1}$은 X가 한단위 증가할때 Y가 평균적으로 변화하는 양이라고 했었는데, 이 로지스틱 회귀 모델의 경우 X가 한단위 증가할때 (4.4) 로그 오즈를 $\beta_{1}$만큼 바꾸며 (4.3)의 오즈에 $e^{\beta_{1}}$을 곱한것과 같다고 할 수 있겠습니다. 하지만 (4.2)에서 X와 p(X)의 관계는 직선이 아니다 보니 X가 한 단위 증가해도 $\beta_{1}$만큼 p(X)를 바꾸지를 못합니다.
p(X)가 변하는 크기는 현재 X의 값이 어떤지에 영향을 받습니다. 하지만 X가 어떤지간에 $\beta_{1}$이 양수인 경우 X가 증가하면 p(X)도 상승할 것이며, $\beta_{1}$이 음수인경우 X가 증가하더라도 p(X)는 감소할 것입니다. X와 p(X)사이 선형적인 관계가 존재하지 않으며, p(X)의 변화율은 현재 X의 값에 따라 정해지는 내용들은 그림 4.2의 오른쪽 판낼에서 확인할수 있겠습니다.
=> 정리
1. 회귀 모델로 확률을 예측 할 수 있다. (식 4.1)
2. 선형 모델로 확률을 예측하면 음수도 나오고 0과 1 밖을 나가버린다. (그림 4.2)
3. 선형 회귀 모델을 로지스틱 함수에 넣어 0과 1사이 확률 값만 나오게 만들었다 (식 4.2)
4. 선형 회귀 모델은 선형적으로 변하나, 로지스틱 회귀 모델은 현재 값에 따라 변함의 정도가 다르다.
- X가 한단위 증가할 떄 단순 선형 회귀 모델은 $\beta_{1}$만큼 Y가 바뀐다.
- 로지스틱 회귀 모델은 $\beta_{1}$만큼 로짓이 바뀐다. => 실제 p(X)는 X와 다르게 변한다.
4.3.2 회귀 계수 추정하기 Estimating the Regression Coefficients
식 (4.2)의 회귀 계수 $\beta_{0}$, $\beta_{1}$은 모르지만 훈련 데이터셋으로 추정해야 합니다. 3장에서는 아직 모르는 선형 회귀 계수들을 추정하기 위해 최소제곱법을 사용했지만. 식 (4.4)같은 모델도 (비선형) 최소 제곱법을 사용할 수 있기는 하지만 일반적으로는 최대 가능도 법 maximum likelihood이 잘 사용되고 있습니다.
로지스틱 회귀 모델을 학습하기 위해서 최대 가능도법을 사용하는 기본 개념은 (4.2)의 식을 사용해서 모든 사람의 예측 확률 $\hat{p}$($x_{i}$)이 실제 관측치에 가장 가깝도록 하는 계수 추정치들을 구하는 방법입니다. 다시 말하면 실제 디폴트인 사람들에 대한 확률이 1이 많이 나오도록 하는 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$를 찾는거에요. 이 개념을 수식화 할수 있으며 이걸 가능도 함수 likelihood function이라고 부릅니다.
$\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$는 이 우도 함수로 최대화 시키고자 할 계수들이구요. 최대 우도법은 이 책 전반에서 다룰 수많은 비선형 적인 방법들을 학습시키는데 널리 사용되고 있습니다. 선형 회귀에서는 최소 제곱법이 사용되었는데, 최대 가능도 법의 특수한 케이스라고 할수 있어요. 최대 가능도법에 대한 수학적으로 자세한 설명은 이책 범위 밖이지만 R 같은 통계적 소프트웨어 패키지에서 사용해서 쉽게 로지스틱 회귀나 다른 모델들을 학습시킬수가 있어요. 그러니 최대 가능도법을 이용한 학습과정의 자세한 사항들에 대해서 걱정할 필요는 없습니다.

표 4.1에서는 카드 대금으로 디폴트=Yes일 확률을 예측하는 로지스틱 회귀 모델 학습 결과로 회귀 계수 추정치와 관련 정보들을 보여주고 있습니다 $\widehat{\beta}_{1}$ = 0.0055는 입력이 증가할때 디폴트 증가 확률과 관련이 되어있으며, 정확하게 얘기하자면 입력이 한 단위 증가할때 디폴트의 로그 오즈가 0.0055 만큼 증가합니다.
표 4.12에서는 로지스팀 회귀 모델의 다른 결과 값들도 보여주고 있으며 3장의 결과물과 비슷합니다. 예를들어 표준 오차 를 계산하여 추정 계수의 정확도를 측정할수 있을 것이고, 표 4.1의 z통계량은 선형 회귀에서 t 통계량과 같은 역활을 하는데 페이지 68의 표 3.1에서 볼수 있습니다. $\beta_{1}$에대한 z통계량은 $\widehat{\beta}_{1}$/ SE($\widehat{\beta}_{1}$과 같으며, z통계량이 클 수록 귀무 가설 $H_{0}$ : $\beta_{1}$ = 0이다. 즉, 채무 확률은 카드 대금에 영향을 받지 않는다 상관없다 라는 귀무가설이 틀렸다고 할 수 있습니다. 카드 대금에 대한 유의확률 p value는 매우 작으므로 귀무 가설 $H_{0}$를 기각 할 수 있고, 다시말하면 카드 대금과 디폴트 확률 사이에는 유의미한 관계가 있다고 볼수있습니다. 표 4.1의 추정 절편은 중요치 않으므로 넘어가겠습니다.
=> 정리
- 로지스틱 회귀 모델의 회귀 계수는 최대 우도법으로 추정한다.
- 최대 우도법을 이용한 계수 추정은 다양한 통계 소프트웨어에서 제공하니 넘어감.
- X가 1씩 증가할때 채무 불이행 확률의 로그 오즈가 0.0055가 증가한다.
4.3.3 예측 하기 Making Predictions
회귀 계수들을 추정하면 카드 대금에 따른 디폴트 확률은 쉽게 계산할 수 있습니다. 표 4.1의 계수 추정치를 이용해서 카드 대금에 대해 X가 $1,000일 때 디폴트 확률을 아래와 같이 구할 수 있는데 아직 확률은 1%보다 낮습니다.

하지만 카드 대금이 $2,000인 경우에는 58.6%로 훨씬 커지게 되요.
3.3.1장에서 본 가변수 방법으로 로지스틱 회귀 모델을 예측할 수도 있겠는데, 예를 들면 학생 여부를 이용하여 디폴트를 판단한다고 해보겠습니다. 이 모델을 학습하기 위해선 학생인경우 1, 학생이 아닌 경우 0으로 두고 가변수를 만들어 모델을 학습하면 되요.


그러면 학생인 경우 채무 불이행할 확률에 대한 로지스틱 회귀 모델의 결과는 표 4.2에서 볼수 있겠습니다. 이 경우는 학생인 경우에 대한 계수들로 보여주고 있는데 p value가 통계적으로 유의미한 것을 볼수 있습니다. 이는 학생이 아닌 경우보다 학생일때 디폴트할 확률이 더 크다는걸 알려줘요.
'번역 > 통계적학습법개론' 카테고리의 다른 글
| [통계기반학습개론] 4.5 분류 기법들 비교하기와 5. 리샘플링 방법 (0) | 2021.02.23 |
|---|---|
| [통계기반학습개론] 4.3.4 다중 로지스틱 회귀와 선형/이차 판별 분석 (0) | 2021.02.21 |
| [통계기반학습개론] 3.4 마케팅 전략/3.5 KNN과 선형 회귀 모델 비교 (0) | 2021.02.06 |
| [통계기반학습개론] 3.2.2 & 3.3 회귀 모델에 대한 중요한 질문들과 다른 고려사항들 (0) | 2021.02.06 |
| [통계기반학습개론] 3.2 다중 선형 회귀 Multiple Linear Regression (0) | 2021.01.31 |