[통계기반학습개론] 5.1.2 LOOCV 하나만 가지고 교차검증, 5.1.3 K-폴드 교차 검증

 

 

5.1.2  Leave-One-Out Cross-Validation

 

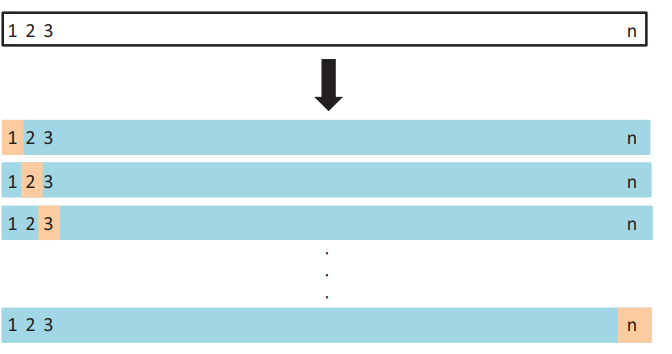
 LOOCV Leave-one-out cross-validation은 5.1.1장에서 본 검증 방법과 비슷한 방법이나 그 방법의 결점을 개선한 것으로 교차 검증셋 방법처럼 LOOCV도 전체 데이터를 두 파트로 나누지만, 어느 정도의 크기의 하부 집합으로 분할하는게 아니라 하나의 데이터 ($x_{1}$, $y_{1}$)만 검증 셋으로 사용하고 나머지 {($x_{2}$, $y_{2}$, . . ., ($x_{n}$, $y_{n}$))}은 훈련셋으로 사용하는 방법입니다. 그래서 통계적 학습 방법을 이용하여 n - 1개의 훈련 데이터들을 학습하고, 1개의 데이터 $x_{1}$으로 $\widehat{y}_{1}$을 예측하게 되요.

 

 

 

 ($x_{1}$, $y_{1}$)만 훈련 과정에서 사용되지 않다보니 $MSE_{1}$ = ($y_{1}$ - $\widehat{y}_{1}$ $)^{2}$은 불편향 추정량인 테스트 에러가 됩니다. 그리고 하나의 데이터만 가지고 테스트를 추정기에는 변동이 큰 문제가 있겠습니다. 이 과정을 ($x_{2}$, $y_{2}$)을 검증셋으로 사용하고 나머지 n - 1개를 훈련으로 사용해서$MSE_{2}$ = ($y_{2}$ - $\widehat{y}_{2}$ $)^{2}$ 를 계산할 수가 있겠습니다. 그래서 이 제곱 오차를 n번 구할수가 있고 $MSE_{1}$, $MSE_{2}$, . . . , $MSE_{n}$을 구해서 이 n 개의 테스트 에러 추정치를 평균으로하여 LOOCV 추정량을 계산 할 수가 있겠습니다.

 

그림 5.3 LOOCV 개요도. n개의 데이터를 가지고 데이터 1개를 검증셋(주황색), 나머지 n - 1개의 데이터들을 훈련셋으로 사용함. 테스트 에러는 n개의 MSE의 평균을 구하여 계산한다. 

 

* LOOCV에 대한 내용은 여기까지만*

 

 

 

 

5.1.3 K-폴드 교차 검증

 

 이번에 볼 LOOCV(생략)의 대안으로 사용할 수 있는 방법으로 k-fold 교차 검증 방법이 있다. 이 방법은 전체 데이터들을 동일한 사이즈를 가지는 k개의 그룹(폴드)로 무작위로 나누고 한 폴드는 검증 데이터셋 나머지 k - 1개의 폴드들은 학습하는데 사용하는 방법이다.

 

 평균 제곱 오차 MSE는 각 폴드들은 한번은 검증 데이터셋, 나머지는 학습 셋으로 사용되도록 하여 전체 k번을 반복하며 각 k 번째 폴드의 $MSE_{1}$, $MSE_{2}$, . . ., $MSE_{k}$의 평균을 구하는 식으로 K-폴드 검증 테스트 에러를 구한다.

 

그림 5.5 이 그림은 5-폴드 교차검증의 개요도로. 전체 데이터들을 겹치지 않는 5개의 그룹으로 분할한다. 각 분할된 폴드(베이지)는 검증셋으로 사용되고, 그 이외는 훈련셋(파란색)으로 사용된다. 테스트 에러는 각 폴드들의 MSE를 평균으로 계산한다.

 LOOCV는 K-폴드 교차검증에서 k를 n으로 설정한거라고 할수 있는데, k-폴드 교차검증에서는 k = 5 혹은 k = 10이라는 식으로 사용한다. k = n이 아닌, k = 5 또는 k = 10으로 지정해서 사용ㅇ하는 경우 이점은 어떤게 있을까? 가장 명확한 장점은 계산 성능이라고 할수 있겠다. LOOCV는 학습과정에 n번을 수행하여야 하다보니 계산 비용이 아주 클수가 있다.

 

 하지만 교차 검증은 어떤 통계적 학습 방법이던 간에 사용할수 있는 방법이기도 한데, 일부 학습 방법의 경우 계산 비용이 아주 클수가 있고, 그래서 LOOCV는 특히 n이 큰 경우에 계산비용적으로 문제가 될수 있다.

 

 하지만 이와 반대로 10-폴드 교차검증의 경우에는 학습 과정을 10번만 하면 되다보니, n보다는 더 계산할수 있으며, 5.1.4장에는 5-폴드 혹은 10-폴드 교차검증의 계산과 관련되지 않은 장점들 편향-분산의 트레이드오프를 보겠다.

 

그림 5.4 차량 데이터셋에서 마력에 대한 다항함수로 mpg를 얼마나 잘 예측하는지를 보기 위해 테스트 에러를 계산하도록 교차검증이 사용됨. 좌측 : LOOCV 곡선, 우측 : 10폴드 교차검증으로 구한 결과. 우측의 계산 결과들은 조금씩 다르게 나오고 있다.

 그림 5.4의 우측 판낼은 10-폴드 교차검증으로 구한 9개의 테스트 에러 결과인데, 10폴드로 나누어서 학습하고 검증시킨 결과에 약간의 변동이 있는걸 볼수 있다. 하지만 이 변동은 그림 5.2의 오른쪽 판낼에서 볼 수 있는 검증셋 방법(홀드 아웃 방법)보다 테스트 에러에서 변동이 일반적으로는 더 작다.

 

  실제 데이터를 사용하는 경우, 우리는 실제 테스트 MSE를 모르다보니 교차 검증의 결과가 얼마나 정확한지를 판단하기는 어려우나 시뮬레이션으로 생성한 데이터를 사용하는 경우 실제 Test MSE를 계산할수 있고 교차 검증의 결과가 얼마나 정확한지 평가할 수 있다.

 

그림 5.6 그림 2.9, 2.10, 2.11에서 사용한 시뮬레이션 데이터의 실제 그리고 추정 테스트 MSE. 실제 MSE는 파란색 선이고, LOOCV로 구한 결과는 검은 점선, 10-폴드 교차 검증으로 구한 결과는 주황색이다. 그리고 X 표시된 지점은 각 MSE곡선이 최저인 지점들을 표기하였다.

 그림 5.6은 2장에서 본 그림 2.9 ~ 2.11에서 사용된 시뮬레이션된 데이터를 가지고 교차 검증/실제 테스트 에러율을 보여주고 있습니다. 여기서 실제 테스트 에러율은 파란선이고, 검은 점선과 주황 선은 LOOCV와 10-폴드 교차검증 추정 MSE가 됩니다.

 

 세 플롯들 다 두 교차 검증 추정량은 비슷하지만 그림 5.6의 오른쪽 판낼에서 실제 테스트 에러율과 교차 검증 테스트 에러율이 아주 비슷한 것을 볼 수 있습니다. 그림 5.6의 중간 판낼의 경우 두 교차 검증 곡선은 차수/유연성이 낮을때는 비슷하지만 유연성/차수가 높을때 테스트 에러율을 과대 추정하고 있습니다. 그림 5.6의 왼쪽 판낼은 교차 검증 곡선들을 형태는 올바르지만 실제 테스트 MSE를 과소 추정하고 있는걸 볼 수 있습니다.

 

 이런 교차 검증을 사용해서 테스트 MSE 추정치를 계산을 하는게 목표가 될 수도 있고, 테스트 MSE 커브의 최소가 되는 지점을 찾는게 목표가 될수도 있겠습니다.  이 지점은 다양한 차수/복잡도를 가지는 모델을 교차검증으로 구할수가 있습니다. 그림 5.6에서처럼 어떤 경우 테스트 MSE 곡선이 실제 테스트 MSE를 과소 평가할때도 있지만, 모든 교차 검증 곡선들은 복잡도에 따라 동일한 형태를 보이며 이를 통해서 가장 작은 테스트 MSE를 찾을수가 있겠습니다.