점유 격자 지도 작성과 역 관측 모델
점유 격자 지도작성 알고리즘은 아래의 주변화된 역 관측 모델 marginalized inverse measurement을 필요로 합니다.
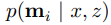
결합 확률, 주변 확률, 조건부 확률
- 결합 확률 joint probability : p(a , b) - 사건 a와 b가 동시에 일어날 확률
- 주변 확률 marginal probability : p(a), p(b) - 사건 a와 b가 결합되지 않은 개별 확률
- 조건부 확률 conditional probability : p(a | b) - 사건 b가 일어났을때 a가 발생할 확률
역 관측 모델
여기서 역이란 의미는 결과로 부터 원인을 찾아내는 것으로
관측치를 이용해서 실제 세계, 주변 환경에 대한 정보를 얻을 수 있습니다.
역 주변 모델과 역 완전 모델
주변 역 관측 모델은 각각의 그리드 셀들의 확률 분포를 말하며, 완전 역 관측 모델은 전체 지도에 대한 확률 분포가 됩니다. 아래는 완전 역 관측 모델과 같습니다.
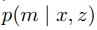
관측 모델로 역 관측 모델 구하기
관측 모델에 대한 식을 이용하여 역 관측모델에 대한 식으로 아래와 같이 정리할 수 있습니다. 여기서 로봇의 자세 정보는 필요없다고 하고 p(m | x) = p(m)이라 합시다.
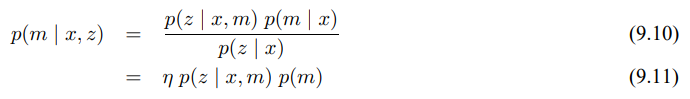
주변화된 역 관측 모델
i번째 그리드 셀에 대한 역 모델은 아래의 식과 같습니다.

기존 관측 모델로 역 센서 모델 학습시키기
관측 모델로 샘플들을 생성시키고, 함수 근사기로 역 모델을 학습 시킬 수 있습니다.
표준 점유 격자 지도작성 알고리즘 특징
지도의 사후확률 추정을 수많은 단일 셀에 대한 사후확률 추정 문제로 변환함으로서
각각의 점유 추정값들 간에 의존관계가 존재하지 않습니다.
완전 지도 사후확률 full map posterior
완전 지도 사후확률은 격자로 정의되는 지도가 크기 때문에
보통 계산이 불가능하나, 최대화 시킬수 있습니다.
최대화를 통해 데이터에 일관적인 지도를 구할수 있습니다.
하지만 최대화시 가능한 모든 데이터를 사용해야하고,
지도 상에 존재하는 불확실성을 놓칠수가 있습니다.
아래의 그림은 (a) 관측치, (b) 기존 점유 격자 지도 알고리즘 (c) 지도 사후확률 최대화 결과 (d) 우도 함수로 불확실성을 가지고 있는 지도.

'로봇 > 로봇' 카테고리의 다른 글
| 파이썬 로보틱스 - SLAM 개요 (0) | 2020.07.06 |
|---|---|
| 파이썬 로보틱스 - 지도작성, 라이다 데이터를 격자 지도로 (0) | 2020.07.06 |
| 파이썬 로보틱스 - 지도 작성, 광선 투사 격자 지도 작성 (0) | 2020.07.04 |
| 파이썬 로보틱스 - 광선 투사와 관측 모델 (0) | 2020.07.04 |
| 파이썬 로보틱스 - 지도작성, 가우시안 그리드 맵 (0) | 2020.07.04 |