지난번에는
앞으로 정리할 지도 작성 예제들과
기본적인 점유 격자 지도작성 알고리즘에 대해서 알아보았고,
이번에는 가우시안 그리드맵에 대해 살펴보겠습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
EXTEND_AREA = 10.0 # [m] grid map extention length
show_animation = True
일단 임포트하는 라이브러리랑
기본 파라미터로 추가 길이를 선언해주는데
뒤에서 천천히 살펴봐야겠습니다.
메인으로 넘어와서 보면
def main():
print(__file__ + " start!!")
xyreso = 0.5 # xy grid resolution
STD = 5.0 # standard diviation for gaussian distribution
for i in range(5):
ox = (np.random.rand(4) - 0.5) * 10.0
oy = (np.random.rand(4) - 0.5) * 10.0
gmap, minx, maxx, miny, maxy = generate_gaussian_grid_map(
ox, oy, xyreso, STD)
if show_animation: # pragma: no cover
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heatmap(gmap, minx, maxx, miny, maxy, xyreso)
plt.plot(ox, oy, "xr")
plt.plot(0.0, 0.0, "ob")
plt.pause(1.0)
if __name__ == '__main__':
main()
루프를 돌리기 전에
해상도와 가우시안 분포 표준 편차를 설정해 줍니다.
이전에 본 위치 추정 애니메이션과는 달리
5번만 반복수행하나 봅니다.
이제 루프 내부 위주로 보겠습니다.
for i in range(5):
ox = (np.random.rand(4) - 0.5) * 10.0
oy = (np.random.rand(4) - 0.5) * 10.0
gmap, minx, maxx, miny, maxy = generate_gaussian_grid_map(
ox, oy, xyreso, STD)
내부 루프에 애니메이션 조건문을 빼고 보면
균일 분포 4개 데이터를 만들고 - 0.5를 해주면
4개의 리스트가 -0.5 ~ 0.5사이 값이 될것이고
*10.0을 하였으니
나오는 값은 x와 y에 대해 (4, )의 -5.0 ~ 5.0 사이 값이 되겠습니다.
이제 가우시안 그리드 맵 함수를 보겠습니다.
def generate_gaussian_grid_map(ox, oy, xyreso, std):
minx, miny, maxx, maxy, xw, yw = calc_grid_map_config(ox, oy, xyreso)
gmap = [[0.0 for i in range(yw)] for i in range(xw)]
for ix in range(xw):
for iy in range(yw):
x = ix * xyreso + minx
y = iy * xyreso + miny
# Search minimum distance
mindis = float("inf")
for (iox, ioy) in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if mindis >= d:
mindis = d
pdf = (1.0 - norm.cdf(mindis, 0.0, std))
gmap[ix][iy] = pdf
return gmap, minx, maxx, miny, maxy
이 함수에서는 우선 그리드 맵 컨피그 계산 부터 하게되는데,
4개의 랜드마크와 해상도를 사용하나 봅니다.
아직 정확하게 어떤건지는 모르겠지만
우선 해당 함수 내부에서 살펴봅시다.
def calc_grid_map_config(ox, oy, xyreso):
minx = round(min(ox) - EXTEND_AREA / 2.0)
miny = round(min(oy) - EXTEND_AREA / 2.0)
maxx = round(max(ox) + EXTEND_AREA / 2.0)
maxy = round(max(oy) + EXTEND_AREA / 2.0)
xw = int(round((maxx - minx) / xyreso))
yw = int(round((maxy - miny) / xyreso))
return minx, miny, maxx, maxy, xw, yw최소 ox - 10/2.0
최소 oy - 10/2.0
....
격자 지도 설정 계산 함수는
사용할 격자 지도의 크기를 설정해주는 함수였네요
격자의 최대 최소 범위 min xy, max xy
격자 갯수 xw, yw
이런 지도 설정을 가지고 다시 지도 작성 함수로 돌아갑시다.
def generate_gaussian_grid_map(ox, oy, xyreso, std):
minx, miny, maxx, maxy, xw, yw = calc_grid_map_config(ox, oy, xyreso)
gmap = [[0.0 for i in range(yw)] for i in range(xw)]
for ix in range(xw):
for iy in range(yw):
x = ix * xyreso + minx
y = iy * xyreso + miny
# Search minimum distance
mindis = float("inf")
for (iox, ioy) in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if mindis >= d:
mindis = d
pdf = (1.0 - norm.cdf(mindis, 0.0, std))
gmap[ix][iy] = pdf
return gmap, minx, maxx, miny, maxy그리드 지도 설정 후에는
중첩 반복문으로 xw, yw로 모든 셀의 값이 0.0인 격자 지도가 만들어집니다.
이 함수의 반복문 내부를 보면
for ix in range(xw):
for iy in range(yw):
x = ix * xyreso + minx
y = iy * xyreso + miny
# Search minimum distance
mindis = float("inf")
for (iox, ioy) in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if mindis >= d:
mindis = d
pdf = (1.0 - norm.cdf(mindis, 0.0, std))
gmap[ix][iy] = pdfminx = -10, xyreso = 0.5, ix = 1 이면
x = -10 + 0.5 = -9.5
ox, oy는 랜드마크의 좌표값으로
zip으로 묶어주면 각 랜드마크들의 리스트가 만들어 집니다.

for ix in range(xw):
for iy in range(yw):
x = ix * xyreso + minx
y = iy * xyreso + miny
# Search minimum distance
mindis = float("inf")
for (iox, ioy) in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if mindis >= d:
mindis = d
pdf = (1.0 - norm.cdf(mindis, 0.0, std))
gmap[ix][iy] = pdf첫번째 격자와 랜드마크 사이 거리 d를 계산해주고,
minds는 처음에 inf 이므로 이후에 mindis = d가 되겠습니다.
4개의 랜드마크에 대해 반복 하면
첫번째 셀에 가장 가까운 랜드마크의 거리가 구해질겁니다.
하지만 첫번째 셀이랑 가장 가까운 거리가 매우 멀다고 가정하고,
예를들어 10이라면 cdf는 1에 가까운 값이 될것이며
확률밀도함수 pdf는 0에 가까운 값이 될것입니다.
즉 이 함수는 랜드마크와 가장 가까운 셀일수록
높은 확률값을 가지게 됩니다.
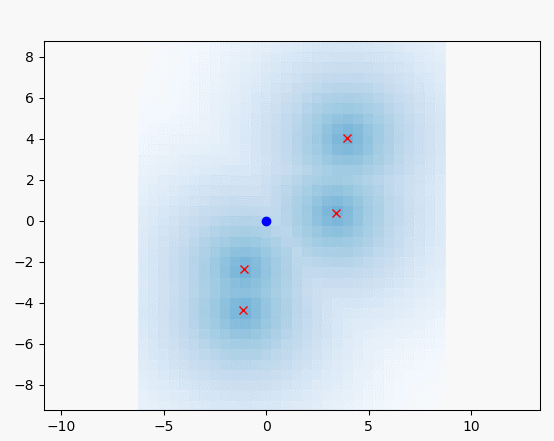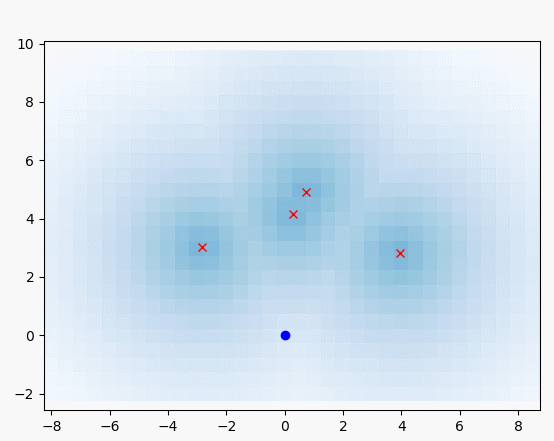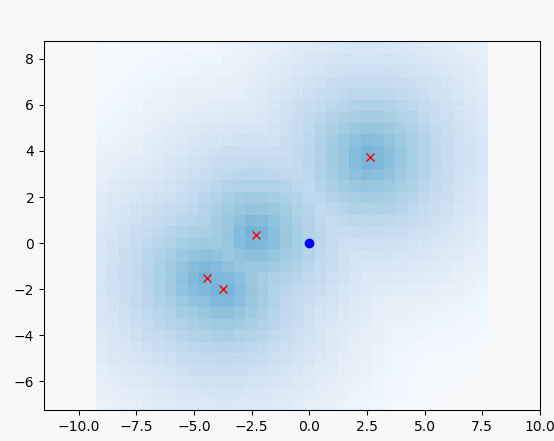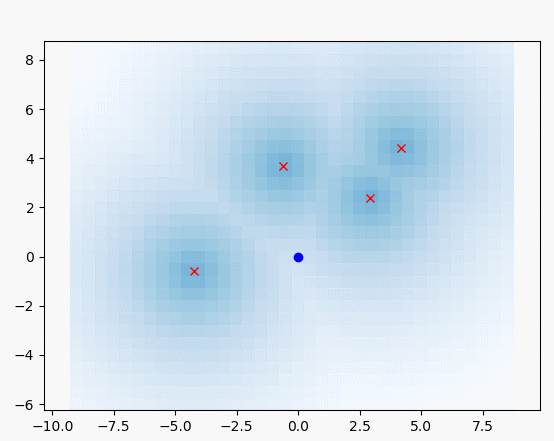
"""
2D gaussian grid map sample
author: Atsushi Sakai (@Atsushi_twi)
"""
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
EXTEND_AREA = 10.0 # [m] grid map extention length
show_animation = True
def generate_gaussian_grid_map(ox, oy, xyreso, std):
minx, miny, maxx, maxy, xw, yw = calc_grid_map_config(ox, oy, xyreso)
gmap = [[0.0 for i in range(yw)] for i in range(xw)]
for ix in range(xw):
for iy in range(yw):
x = ix * xyreso + minx
y = iy * xyreso + miny
# Search minimum distance
mindis = float("inf")
for (iox, ioy) in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if mindis >= d:
mindis = d
pdf = (1.0 - norm.cdf(mindis, 0.0, std))
gmap[ix][iy] = pdf
return gmap, minx, maxx, miny, maxy
def calc_grid_map_config(ox, oy, xyreso):
minx = round(min(ox) - EXTEND_AREA / 2.0)
miny = round(min(oy) - EXTEND_AREA / 2.0)
maxx = round(max(ox) + EXTEND_AREA / 2.0)
maxy = round(max(oy) + EXTEND_AREA / 2.0)
xw = int(round((maxx - minx) / xyreso))
yw = int(round((maxy - miny) / xyreso))
return minx, miny, maxx, maxy, xw, yw
def draw_heatmap(data, minx, maxx, miny, maxy, xyreso):
x, y = np.mgrid[slice(minx - xyreso / 2.0, maxx + xyreso / 2.0, xyreso),
slice(miny - xyreso / 2.0, maxy + xyreso / 2.0, xyreso)]
plt.pcolor(x, y, data, vmax=1.0, cmap=plt.cm.Blues)
plt.axis("equal")
def main():
print(__file__ + " start!!")
xyreso = 0.5 # xy grid resolution
STD = 5.0 # standard diviation for gaussian distribution
for i in range(5):
ox = (np.random.rand(4) - 0.5) * 10.0
oy = (np.random.rand(4) - 0.5) * 10.0
gmap, minx, maxx, miny, maxy = generate_gaussian_grid_map(
ox, oy, xyreso, STD)
if show_animation: # pragma: no cover
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heatmap(gmap, minx, maxx, miny, maxy, xyreso)
plt.plot(ox, oy, "xr")
plt.plot(0.0, 0.0, "ob")
plt.pause(1.0)
if __name__ == '__main__':
main()'로봇 > 로봇' 카테고리의 다른 글
| 파이썬 로보틱스 - 지도 작성, 광선 투사 격자 지도 작성 (0) | 2020.07.04 |
|---|---|
| 파이썬 로보틱스 - 광선 투사와 관측 모델 (0) | 2020.07.04 |
| 파이썬 로보틱스 - 점유 격자 지도 작성 알고리즘 복습 (0) | 2020.07.04 |
| 파이썬 로포틱스 - 맵핑 예제들 (0) | 2020.07.04 |
| 파이썬 로보틱스 - 위치추정, 히스토그램 필터 (0) | 2020.07.04 |