지난번에는
연속 공간에서의 위치 추정 문제를 다루는
확장 칼만 필터와 파티클 필터를 이용한 위치 추정 시뮬레이션을 동작 시켜보았습니다.
이번에는 히스토그램 필터에 대해서 살펴보겠습니다.
히스토그램 필터는 파티클 필터처럼 가우시안 모델을 사용하지 않는 비모수적인 필터 중 하나로
상태 공간을 유한개의 영역들로 나누고, 사후 확률을 각 영역들의 확률 값으로 나타내는 방법입니다.
이 작업이 이산 영역에 적용되면 이산 베이즈 필터, 연속 공간에서 적용이되면 히스토그램이라 부르개 됩니다.
이산 베이즈 필터를 본 후 연속 공간에 대한 히스토그램을 봅시다.
우선 이산 베이즈 필터는 2장에서 살펴본 베이즈 필터의 적분을
유한 합에 대한 식으로 수정한 것으로 아래와 같습니다.

이제 이 이산 베이즈 필터를 연속 상태 공간에서 근사 추론을 하는 도구로 사용을 할것이며, 이 필터를 히스토그램 필터라고 부릅니다.
히스토그램은 연속 상태공간을 유한개의 많은 영역으로 분해하므로 아래와 같이 정리할수 있겠습니다.
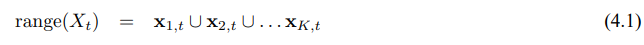
우선 처음에는 이산 베이즈 필터가 신뢰도 분포에 아무런 정보를 주지 못하므로, 각 영역에 대한 상태들이 균일 확률 분포가 되어 사후 확률은 상수 확률 밀도 함수가 됩니다. (우항의 분모는 해당 영역의 크기)

위 식에서 이산 베이즈 필터를 균일 분포를 사용하여 다음의 근사화 결과를 구할수 있습니다.


히스토그램에 대해 간단히 여기까지 살펴보고 히스토그램 필터 시뮬레이션 코드를 살펴보겠습니다.
# Parameters
SIM_TIME = 10.0 # simulation time [s]
DT = 0.1 # time tick [s]
MAX_RANGE = 10.0 # maximum observation range
MOTION_STD = 1.0 # standard deviation for motion gaussian distribution
RANGE_STD = 3.0 # standard deviation for observation gaussian distribution
# grid map param
XY_RESOLUTION = 0.5 # xy grid resolution
MIN_X = -15.0
MIN_Y = -5.0
MAX_X = 15.0
MAX_Y = 25.0
# simulation parameters
NOISE_RANGE = 2.0 # [m] 1σ range noise parameter
NOISE_SPEED = 0.5 # [m/s] 1σ speed noise parameter
show_animation = True
- 기본 파라미터
일단 시뮬레이션 시간은 10초
시간 간격은 0.1초
최대 측정 거리 10m
동작 모델 노이즈 가우시안 분포 표준편차 1.0
측정 모델 노이즈 가우시안 분포 표준편차 3.0
- 격자 지도 파라미터
지도 해상도는 0.5
x : -15 ~ 15
y : -5 ~ 25
- 시뮬레이션 파라미터
관측 노이즈 2.0
속도 노이즈 0.5
class GridMap:
def __init__(self):
self.data = None
self.xy_resolution = None
self.min_x = None
self.min_y = None
self.max_x = None
self.max_y = None
self.x_w = None
self.y_w = None
self.dx = 0.0 # movement distance
self.dy = 0.0 # movement distance일단 그리드맵 클래스 구조는 위와 같습니다.
일단 main함수에서 순서대로 따라가봅시다.
def main():
print(__file__ + " start!!")
# RF_ID positions [x, y]
RF_ID = np.array([[10.0, 0.0],
[10.0, 10.0],
[0.0, 15.0],
[-5.0, 20.0]])
time = 0.0
xTrue = np.zeros((4, 1))
grid_map = init_grid_map(XY_RESOLUTION, MIN_X, MIN_Y, MAX_X, MAX_Y)
mx, my = calc_grid_index(grid_map) # for grid map visualization
while SIM_TIME >= time:
time += DT
print("Time:", time)
u = calc_input()
yaw = xTrue[2, 0] # Orientation is known
xTrue, z, ud = observation(xTrue, u, RF_ID)
grid_map = histogram_filter_localization(grid_map, u, z, yaw)
if show_animation:
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heat_map(grid_map.data, mx, my)
plt.plot(xTrue[0, :], xTrue[1, :], "xr")
plt.plot(RF_ID[:, 0], RF_ID[:, 1], ".k")
for i in range(z.shape[0]):
plt.plot([xTrue[0, :], z[i, 1]], [
xTrue[1, :], z[i, 2]], "-k")
plt.title("Time[s]:" + str(time)[0: 4])
plt.pause(0.1)
print("Done")
if __name__ == '__main__':
main()
메인 전체에서 루프 이전 내용들을 살펴보겠습니다.
def main():
print(__file__ + " start!!")
# RF_ID positions [x, y]
RF_ID = np.array([[10.0, 0.0],
[10.0, 10.0],
[0.0, 15.0],
[-5.0, 20.0]])
time = 0.0
xTrue = np.zeros((4, 1))
grid_map = init_grid_map(XY_RESOLUTION, MIN_X, MIN_Y, MAX_X, MAX_Y)
mx, my = calc_grid_index(grid_map) # for grid map visualization
중요한 부분만 짚고 넘어가면
1. 관측할 RF_ID 4개 위치를 초기화
2. 실제 로봇의 상태 공간 초기화
3. 그리드맵 초기화
4. 그리드 인덱스 계산
일단 그리드맵 초기화 부분을 살펴보면
def init_grid_map(xy_resolution, min_x, min_y, max_x, max_y):
grid_map = GridMap()
grid_map.xy_resolution = xy_resolution
grid_map.min_x = min_x
grid_map.min_y = min_y
grid_map.max_x = max_x
grid_map.max_y = max_y
grid_map.x_w = int(round((grid_map.max_x - grid_map.min_x)
/ grid_map.xy_resolution))
grid_map.y_w = int(round((grid_map.max_y - grid_map.min_y)
/ grid_map.xy_resolution))
grid_map.data = [[1.0 for _ in range(grid_map.y_w)]
for _ in range(grid_map.x_w)]
grid_map = normalize_probability(grid_map)
return grid_map위에서 정의한 구조체 대로 그리드맵을 생성 후
지정한 파라미터들을 전달하고
x_w, y_w를 계산하는데
x축 경우만 살펴보면
15 - (-15) / 0.5 = 30/0.5 =60
x_w는 x 공간의 개수
y_w는 y 공간의 개수가 될것이고
grid_map.data는 모든 격자의 값이 1인 2차원 격자가 되겠습니다.
def normalize_probability(grid_map):
sump = sum([sum(i_data) for i_data in grid_map.data])
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
grid_map.data[ix][iy] /= sump
return grid_map그 다음 오훌하는 확률 정규화 함수를 보면
모든 행의 합을 구하고
각 격자에 이 합을 나누면서
모든 격자는 균일 분포를 따르게 됩니다.
여기서 x, y 각각 60개 이므로 총 3,600개
하나의 격자는 1/3,600 크기를 가지게 됩니다.
이제 그리드 지도 초기화를 마치고 넘어가봅시다.
def main():
print(__file__ + " start!!")
# RF_ID positions [x, y]
RF_ID = np.array([[10.0, 0.0],
[10.0, 10.0],
[0.0, 15.0],
[-5.0, 20.0]])
time = 0.0
xTrue = np.zeros((4, 1))
grid_map = init_grid_map(XY_RESOLUTION, MIN_X, MIN_Y, MAX_X, MAX_Y)
mx, my = calc_grid_index(grid_map) # for grid map visualization다시 메인으로 돌아와 보면
그리드 인덱스도 계산해줍시다
def calc_grid_index(grid_map):
mx, my = np.mgrid[slice(grid_map.min_x - grid_map.xy_resolution / 2.0,
grid_map.max_x + grid_map.xy_resolution / 2.0,
grid_map.xy_resolution),
slice(grid_map.min_y - grid_map.xy_resolution / 2.0,
grid_map.max_y + grid_map.xy_resolution / 2.0,
grid_map.xy_resolution)]
return mx, my슬라이스 함수부터 보면
min_x 는 -15, resolution = 0.5
-15 - 0.25 = -15.25
-15.25 ~ 15.25간격을 0.5로 나눌것이고
30.5 / 0.5 = 61
길이가 61인 리스트가 반환될것이고
y도 있으니
길이가 61, 61인 리스트가 mgrid의 인자로 사용되겠습니다.
아래의 설명에 따르면 차원을 뻥튀기 해준다고하니
my, my는 둘다 61, 61차원의 값이 되겠습니다.

mx 출력 결과
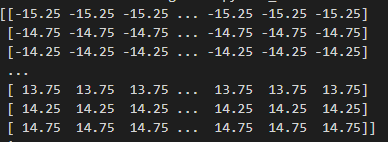
이제 그리드 인덱스 계산까지 마쳤으니 주 루프문을 다시 살펴보겠습니다.
while SIM_TIME >= time:
time += DT
print("Time:", time)
u = calc_input()
yaw = xTrue[2, 0] # Orientation is known
xTrue, z, ud = observation(xTrue, u, RF_ID)
grid_map = histogram_filter_localization(grid_map, u, z, yaw)
if show_animation:
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heat_map(grid_map.data, mx, my)
plt.plot(xTrue[0, :], xTrue[1, :], "xr")
plt.plot(RF_ID[:, 0], RF_ID[:, 1], ".k")
for i in range(z.shape[0]):
plt.plot([xTrue[0, :], z[i, 1]], [
xTrue[1, :], z[i, 2]], "-k")
plt.title("Time[s]:" + str(time)[0: 4])
plt.pause(0.1)
여기서 시각화 하는 부분을 빼면
1. 입력 계산 calc_input
2. 관측 observation
3. 히스토그램 필터 위치추정 histogram_filter_localization
이렇게 3 파트로 나눌수 있겠습니다.
입력 계산을 살펴보겠습니다.
def calc_input():
v = 1.0 # [m/s]
yaw_rate = 0.1 # [rad/s]
u = np.array([v, yaw_rate]).reshape(2, 1)
return u
여기는 속도 기반 모델인지
2,1의 행렬로
첫재 값은 선속도, 둘때 값은 각속도를 넣어서 반환해 줍니다
다음으로 관측을 봅시다
def observation(xTrue, u, RFID):
xTrue = motion_model(xTrue, u)
z = np.zeros((0, 3))
for i in range(len(RFID[:, 0])):
dx = xTrue[0, 0] - RFID[i, 0]
dy = xTrue[1, 0] - RFID[i, 1]
d = math.hypot(dx, dy)
if d <= MAX_RANGE:
# add noise to range observation
dn = d + np.random.randn() * NOISE_RANGE
zi = np.array([dn, RFID[i, 0], RFID[i, 1]])
z = np.vstack((z, zi))
# add noise to speed
ud = u[:, :]
ud[0] += np.random.randn() * NOISE_SPEED
return xTrue, z, ud
일단 관측하기전에
실제 상태에 노이즈 없는 입력을 주어
실제 이동 위치를 구하고
실제 이동 위치와 RFID 사이의 거리를 계산하겠습니다.
여기서 구한 거리 d가 관측 가능 거리에 속한다면
관측 노이즈 dn과 가우시안 분포를 곱하여 노이즈를 반영한 실제 측정치가 됩니다.
이 실제 측정치들을 모든 RFID에 구하여 z에 vstack으로 쌓아주면
아마 zi가 거리, rfid x, rfid y이므로 (1, 3)
zi가 4개이니
z는 (4, 3)d의 데이터가 될겁니다.
이제 실제 이동후 위치와 노이즈가 반영된 관측치, 노이즈가 반영된 입력치를 필터에 사용할수있도록 반환해줍시다.
while SIM_TIME >= time:
time += DT
print("Time:", time)
u = calc_input()
yaw = xTrue[2, 0] # Orientation is known
xTrue, z, ud = observation(xTrue, u, RF_ID)
grid_map = histogram_filter_localization(grid_map, u, z, yaw)
if show_animation:
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heat_map(grid_map.data, mx, my)
plt.plot(xTrue[0, :], xTrue[1, :], "xr")
plt.plot(RF_ID[:, 0], RF_ID[:, 1], ".k")
for i in range(z.shape[0]):
plt.plot([xTrue[0, :], z[i, 1]], [
xTrue[1, :], z[i, 2]], "-k")
plt.title("Time[s]:" + str(time)[0: 4])
plt.pause(0.1)
이제 이 시뮬레이션의 핵심인
히스토그램 위치 추정 파트를 살펴보겠습니다.
def histogram_filter_localization(grid_map, u, z, yaw):
grid_map = motion_update(grid_map, u, yaw)
grid_map = observation_update(grid_map, z, RANGE_STD)
return grid_map
히스토그램 필터는 모든 격자에 대해
아래의 이산 베이즈 필터처럼
동작 갱신과 관측 갱신이 수행됩니다.
우선 동작 갱신부터 살펴보겠습니다.

def motion_update(grid_map, u, yaw):
grid_map.dx += DT * math.cos(yaw) * u[0]
grid_map.dy += DT * math.sin(yaw) * u[0]
x_shift = grid_map.dx // grid_map.xy_resolution
y_shift = grid_map.dy // grid_map.xy_resolution
if abs(x_shift) >= 1.0 or abs(y_shift) >= 1.0: # map should be shifted
grid_map = map_shift(grid_map, int(x_shift), int(y_shift))
grid_map.dx -= x_shift * grid_map.xy_resolution
grid_map.dy -= y_shift * grid_map.xy_resolution
grid_map.data = gaussian_filter(grid_map.data, sigma=MOTION_STD)
return grid_map
우선 dx, dy를 계산하는데 초기화 당시에는 값을 넣어주지도 않았고,
첫번째 루프이므로 처음에는 0이 있었을 겁니다.
노이즈 입력치 u와 각 yaw, 시간 간격 dt에 따라 이동 거리가 dx, dy에 들어갈 것이고
일단 yaw는 이동 전에 구했으므로 0
u는 (1.0, 0.1)^T이고, 시간 간격은 0.1이므로
dx, dy는 아무튼 매우 작은 수일 겂니다.
x_shift, y_shift는 이 이동 거리 // 그리드 해상도이므로
이동거리가 어느정도 커지기 전까지는 시프트가 일어나지는 않을것 같습니다.
어느 정도 루프를 돌다보면 이동 거리도 커지고 지도가 시프트 해야 될 때가 올것 같습니다.
이번에는 map_shift 함수를 잠깐 살펴보면
def map_shift(grid_map, x_shift, y_shift):
tmp_grid_map = copy.deepcopy(grid_map.data)
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
nix = ix + x_shift
niy = iy + y_shift
if 0 <= nix < grid_map.x_w and 0 <= niy < grid_map.y_w:
grid_map.data[ix + x_shift][iy + y_shift] =\
tmp_grid_map[ix][iy]
return grid_map우선 그리드 맵의 데이터를 깊은 복사를 수행하네요.
맨 처음에 그리드 맵 데이터들을 균일 분포로 했으므로 각 영역들은 1/3,600의 값을 가지고 있을 겁니다.
그리드 맵 초기화 함수에서 x_w, y_w는 60이었으니
이제 각 그리드 영역에 접근해서 값을 수정하는 작업을 수행할것 같습니다.
일단 x_shift 1, y_shift도 1인 경우를 가정해서 생각해보겠습니다.
루프 안에서 nix, niy 값들은 모두 ix, iy보다 1씩 큰 값을 가지게 될겁니다.
그리고 이 nix와 niy가 각각 x, y 축 범위 안에 속한다면
이전 위치의 값 (0, 0)을 (1,1)을 옮기도록 수행하게 됩니다.
* 조건문 안에 " =\(역슬래시) " 부분을 보고 햇갈렸는데 우항 값이 다음줄로 넘어가기때문에 다음줄의 값을 좌항에다 넣기 위해 =\를 사용한듯합니다.
일단 map_shift 함수는 계산한 x,y_shift에 따라 기존의 맵에 존재하던 값들을 시프트 연산을 해주는게 되겠습니다.
다시 모션 업데이트를 돌아오면
def motion_update(grid_map, u, yaw):
grid_map.dx += DT * math.cos(yaw) * u[0]
grid_map.dy += DT * math.sin(yaw) * u[0]
x_shift = grid_map.dx // grid_map.xy_resolution
y_shift = grid_map.dy // grid_map.xy_resolution
if abs(x_shift) >= 1.0 or abs(y_shift) >= 1.0: # map should be shifted
grid_map = map_shift(grid_map, int(x_shift), int(y_shift))
grid_map.dx -= x_shift * grid_map.xy_resolution
grid_map.dy -= y_shift * grid_map.xy_resolution
grid_map.data = gaussian_filter(grid_map.data, sigma=MOTION_STD)
return grid_map
dx, dy가 무한히 커지는걸 막기위해 지도만 시프트한후
다시 시프트 한 크기만큼 이동 거리를 줄여줍니다.
마지막으로 가우시안 필터를 사용하게 되는데,
이동한 지도에 동작 노이즈만큼 가우시안 노이즈만 추가해주게 됩니다.
이제 이동한 지도 값도 구하고 동작 노이즈도 반영하였으니
관측 갱신 파트를 살펴보겠습니다.
def observation_update(grid_map, z, std):
for iz in range(z.shape[0]):
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
grid_map.data[ix][iy] *= calc_gaussian_observation_pdf(
grid_map, z, iz, ix, iy, std)
grid_map = normalize_probability(grid_map)
return grid_map관측 갱신에서는 기존의 지도, 관측 데이터,
관측 노이즈 표준편차를 사용하여 계산됩니다.
우선 z에 대해서 도는것을 보니 각각의 관측치 데이터를 가지고
전체 격자들의 값들을 변경시키는것 같습니다.
루프문 맨 안에 보면 가우시안 관측 밀도 함수 계산값을 구하여 각 격자 값을 갱신시키고 있습니다.
가우시안 관측 확률 밀도 계산 함수를 살펴보겠습니다.
def calc_gaussian_observation_pdf(grid_map, z, iz, ix, iy, std):
# predicted range
x = ix * grid_map.xy_resolution + grid_map.min_x
y = iy * grid_map.xy_resolution + grid_map.min_y
d = math.hypot(x - z[iz, 1], y - z[iz, 2])
# likelihood
pdf = (1.0 - norm.cdf(abs(d - z[iz, 0]), 0.0, std))
return pdf일단 z는 첫번째 rfid (10, 0)로
여기서 z는 관측 모델에서 구한 (10, 10, 0)으로 가정하겠습니다. (거리, x, y)
ix, iy는 1로 가정하고 살펴봅시다.
x = 1 * 0.5 + (-15) = -14.5일 것이고,
격자 1,1에서 첫번째 랜드마크 사이 거리 d를 구할것이고(예측 거리)
cdf는 누적 정규 분포로 아래의 표를 참고하면 좋겠습니다.
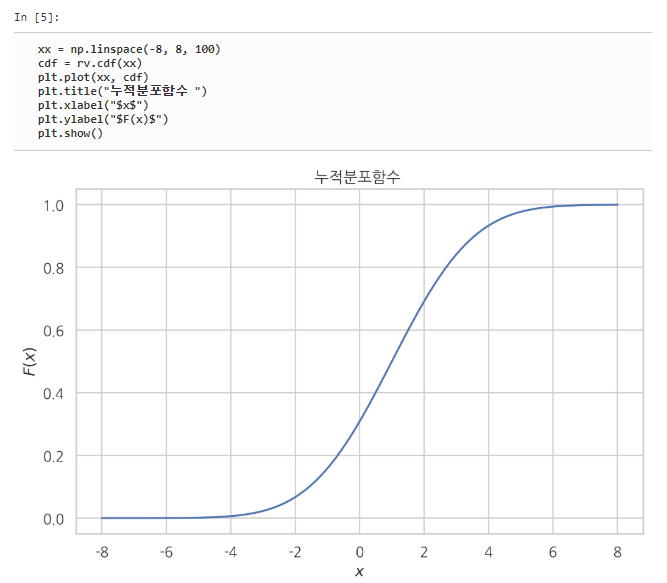
def calc_gaussian_observation_pdf(grid_map, z, iz, ix, iy, std):
# predicted range
x = ix * grid_map.xy_resolution + grid_map.min_x
y = iy * grid_map.xy_resolution + grid_map.min_y
d = math.hypot(x - z[iz, 1], y - z[iz, 2])
# likelihood
pdf = (1.0 - norm.cdf(abs(d - z[iz, 0]), 0.0, std))
return pdf
격자 (1,1)에서 예측 d는 첫번재 랜드마크와 매우 멀으므로
abs(예측 거리 - 실제 거리)는 매우 큰 값이 될것이고,
누적 정규 분포에 따라 1에 가까운 값이 됩니다.
하지만 우도를 계산하는만큼 1 - (1에 가까운 값)이라면 0에 가까운 확률 밀도가 반환되고
결국 (1,1) 격자는 가중치가 매우 작아질겁니다.
하지만 실제 첫번째 랜드마크와 가까운 격자라면
예측 거리 - 실제 거리는 매우 작은 값이 될것이며
높은 pdf 값을 반환한다고 볼수 있겠습니다.
def observation_update(grid_map, z, std):
for iz in range(z.shape[0]):
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
grid_map.data[ix][iy] *= calc_gaussian_observation_pdf(
grid_map, z, iz, ix, iy, std)
grid_map = normalize_probability(grid_map)
return grid_map다시 관측 갱신으로 돌아와
확률 정규화 과정을 시키면
첫번째 루프의 히스토그램 필터 수행이 완료됩니다.
# Parameters
SIM_TIME = 20.0 # simulation time [s]
DT = 0.5 # time tick [s]
MAX_RANGE = 10.0 # maximum observation range
MOTION_STD = 1.0 # standard deviation for motion gaussian distribution
RANGE_STD = 3.0 # standard deviation for observation gaussian distribution
파라미터를 조금 수정해서
동작시켜보겠습니다.

전체 코드 histogram_filter.py
"""
Histogram Filter 2D localization example
In this simulation, x,y are unknown, yaw is known.
Initial position is not needed.
author: Atsushi Sakai (@Atsushi_twi)
"""
import copy
import math
import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import gaussian_filter
from scipy.stats import norm
# Parameters
SIM_TIME = 20.0 # simulation time [s]
DT = 0.5 # time tick [s]
MAX_RANGE = 10.0 # maximum observation range
MOTION_STD = 1.0 # standard deviation for motion gaussian distribution
RANGE_STD = 3.0 # standard deviation for observation gaussian distribution
# grid map param
XY_RESOLUTION = 0.5 # xy grid resolution
MIN_X = -15.0
MIN_Y = -5.0
MAX_X = 15.0
MAX_Y = 25.0
# simulation parameters
NOISE_RANGE = 2.0 # [m] 1σ range noise parameter
NOISE_SPEED = 0.5 # [m/s] 1σ speed noise parameter
show_animation = True
class GridMap:
def __init__(self):
self.data = None
self.xy_resolution = None
self.min_x = None
self.min_y = None
self.max_x = None
self.max_y = None
self.x_w = None
self.y_w = None
self.dx = 0.0 # movement distance
self.dy = 0.0 # movement distance
def histogram_filter_localization(grid_map, u, z, yaw):
grid_map = motion_update(grid_map, u, yaw)
grid_map = observation_update(grid_map, z, RANGE_STD)
return grid_map
def calc_gaussian_observation_pdf(grid_map, z, iz, ix, iy, std):
# predicted range
x = ix * grid_map.xy_resolution + grid_map.min_x
y = iy * grid_map.xy_resolution + grid_map.min_y
d = math.hypot(x - z[iz, 1], y - z[iz, 2])
# likelihood
pdf = (1.0 - norm.cdf(abs(d - z[iz, 0]), 0.0, std))
return pdf
def observation_update(grid_map, z, std):
for iz in range(z.shape[0]):
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
grid_map.data[ix][iy] *= calc_gaussian_observation_pdf(
grid_map, z, iz, ix, iy, std)
grid_map = normalize_probability(grid_map)
return grid_map
def calc_input():
v = 1.0 # [m/s]
yaw_rate = 0.1 # [rad/s]
u = np.array([v, yaw_rate]).reshape(2, 1)
return u
def motion_model(x, u):
F = np.array([[1.0, 0, 0, 0],
[0, 1.0, 0, 0],
[0, 0, 1.0, 0],
[0, 0, 0, 0]])
B = np.array([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT],
[1.0, 0.0]])
x = F @ x + B @ u
return x
def draw_heat_map(data, mx, my):
max_value = max([max(i_data) for i_data in data])
plt.pcolor(mx, my, data, vmax=max_value, cmap=plt.cm.get_cmap("Blues"))
plt.axis("equal")
def observation(xTrue, u, RFID):
xTrue = motion_model(xTrue, u)
z = np.zeros((0, 3))
for i in range(len(RFID[:, 0])):
dx = xTrue[0, 0] - RFID[i, 0]
dy = xTrue[1, 0] - RFID[i, 1]
d = math.hypot(dx, dy)
if d <= MAX_RANGE:
# add noise to range observation
dn = d + np.random.randn() * NOISE_RANGE
zi = np.array([dn, RFID[i, 0], RFID[i, 1]])
z = np.vstack((z, zi))
# add noise to speed
ud = u[:, :]
ud[0] += np.random.randn() * NOISE_SPEED
return xTrue, z, ud
def normalize_probability(grid_map):
sump = sum([sum(i_data) for i_data in grid_map.data])
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
grid_map.data[ix][iy] /= sump
return grid_map
def init_grid_map(xy_resolution, min_x, min_y, max_x, max_y):
grid_map = GridMap()
grid_map.xy_resolution = xy_resolution
grid_map.min_x = min_x
grid_map.min_y = min_y
grid_map.max_x = max_x
grid_map.max_y = max_y
grid_map.x_w = int(round((grid_map.max_x - grid_map.min_x)
/ grid_map.xy_resolution))
grid_map.y_w = int(round((grid_map.max_y - grid_map.min_y)
/ grid_map.xy_resolution))
grid_map.data = [[1.0 for _ in range(grid_map.y_w)]
for _ in range(grid_map.x_w)]
grid_map = normalize_probability(grid_map)
return grid_map
def map_shift(grid_map, x_shift, y_shift):
tmp_grid_map = copy.deepcopy(grid_map.data)
for ix in range(grid_map.x_w):
for iy in range(grid_map.y_w):
nix = ix + x_shift
niy = iy + y_shift
if 0 <= nix < grid_map.x_w and 0 <= niy < grid_map.y_w:
grid_map.data[ix + x_shift][iy + y_shift] =\
tmp_grid_map[ix][iy]
return grid_map
def motion_update(grid_map, u, yaw):
grid_map.dx += DT * math.cos(yaw) * u[0]
grid_map.dy += DT * math.sin(yaw) * u[0]
x_shift = grid_map.dx // grid_map.xy_resolution
y_shift = grid_map.dy // grid_map.xy_resolution
if abs(x_shift) >= 1.0 or abs(y_shift) >= 1.0: # map should be shifted
grid_map = map_shift(grid_map, int(x_shift), int(y_shift))
grid_map.dx -= x_shift * grid_map.xy_resolution
grid_map.dy -= y_shift * grid_map.xy_resolution
grid_map.data = gaussian_filter(grid_map.data, sigma=MOTION_STD)
return grid_map
def calc_grid_index(grid_map):
mx, my = np.mgrid[slice(grid_map.min_x - grid_map.xy_resolution / 2.0,
grid_map.max_x + grid_map.xy_resolution / 2.0,
grid_map.xy_resolution),
slice(grid_map.min_y - grid_map.xy_resolution / 2.0,
grid_map.max_y + grid_map.xy_resolution / 2.0,
grid_map.xy_resolution)]
return mx, my
def main():
print(__file__ + " start!!")
# RF_ID positions [x, y]
RF_ID = np.array([[10.0, 0.0],
[10.0, 10.0],
[0.0, 15.0],
[-5.0, 20.0]])
time = 0.0
xTrue = np.zeros((4, 1))
grid_map = init_grid_map(XY_RESOLUTION, MIN_X, MIN_Y, MAX_X, MAX_Y)
mx, my = calc_grid_index(grid_map) # for grid map visualization
while SIM_TIME >= time:
time += DT
print("Time:", time)
u = calc_input()
yaw = xTrue[2, 0] # Orientation is known
xTrue, z, ud = observation(xTrue, u, RF_ID)
grid_map = histogram_filter_localization(grid_map, u, z, yaw)
if show_animation:
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
draw_heat_map(grid_map.data, mx, my)
plt.plot(xTrue[0, :], xTrue[1, :], "xr")
plt.plot(RF_ID[:, 0], RF_ID[:, 1], ".k")
for i in range(z.shape[0]):
plt.plot([xTrue[0, :], z[i, 1]], [
xTrue[1, :], z[i, 2]], "-k")
plt.title("Time[s]:" + str(time)[0: 4])
plt.pause(0.1)
print("Done")
if __name__ == '__main__':
main()
'로봇 > 로봇' 카테고리의 다른 글
| 파이썬 로보틱스 - 점유 격자 지도 작성 알고리즘 복습 (0) | 2020.07.04 |
|---|---|
| 파이썬 로포틱스 - 맵핑 예제들 (0) | 2020.07.04 |
| 14.6~ 3차원 지도 작성 (0) | 2020.06.29 |
| 14.4 증분 지도작성과 사후확률추정 (0) | 2020.06.29 |
| 확률적 로봇 공학 - 7.6 대응관계 추정 (0) | 2020.06.24 |