14.4 증분 지도 작성과 사후확률 추정 incremental mapping with posterior estimation
이러한 사이클 문제를 극복하려면 과거 자세 추정치 개선이 필요합니다. 이는 데이터가 기억되어야 하는데, 에를들자면 우리가 시간에 대해 각점에서 단일 점유 격자 값만 유지한다면 사이클이 닫힐때 발견되는 불일관성을 따라 그리드를 바꿀수가 없습니다. 그래서 자세가 회상하여 고칠수 있도록 과거의 센서 관측값과 추정 자세를 기억하는게 필수입니다.
14.4.1 사이클 감지
다음으로 살펴볼 매카니즘은 사이클 감지하는것인데, 로봇의 자세에 대한 완전 사후확률을 수행하는 두번째 추정기를 소개하면서 살펴보겠습니다. 사후확률 자세 추정은 위치 추정과 동일합니다. 로봇 위치 추정기는 이미 2~ 7장사이의 내용들로 넓게 살펴봤는데, 이 기본 개념 방정식을 이용해서 다시 간단히 정리하면 다음과 같습니다.

여기서 $x^{(t)}$는 시간 t에서 로봇의 자세가 됩니다. 자세가 주어질때 사후확률 추정하는 알고리즘은 표 7.1에서 볼수 있습니다.
위치 추정을 구현할때 고려해야할것은 이미 로봇의 위치를 추정하는 증분 지도 추정기와 함께 동시적으로 수행되어야 합니다. 최소한 최대 우도 추정기는 비사이클 상황에서 일관성을 가져야만 합니다. 그래서 P($x^{t}$ | $a^{(t-1)}$, $x^{(t-1)}$, m)은 로봇 동작 모델이 아닙니다. 대신 이것은 최대 우도 추정기로 구한 잔여 에러 모델이며, 일관되게 하기 위해서 P($x^{t}$ | $a^{(t-1)}$, $x^{(t-1)}$, m)의 모드는 식 14.13의 최대 우도 자세 추정기의 결과는 같아야 합니다.

조건부 확률의 불확실성은 이 추정의 사후확률 불확실성을 반영하며, 이 불확실성은 0평균 정규 분포를 따른다고 가정할때, 역 공분산 행렬은 식 14.13의 로그 우도 함수의 이차미분에서 복워할수 있습니다. 비슷하게 그동안 살펴본 동작 모델 중 하나를 사용하여 시도하여 동작 노이즈 파라미터를 추측할수도 있습니다. 다른 경우로 P($x^{t}$ | $a^{(t-1)}$, $x^{(t-1)}$, m)는 이 모델은 센서 관측에 의해 자세를 갱신한 후의 불호가실성을 설계하기 때문에 기존의 로봇 동작 모델보다 더 중요한 확률분포가 됩니다.
비슷하게 P($o^{t}$ | $x^{(t)}$, $m^{(t)}$)는 인지 모델이라고 할수 없는데, 이것을 인지 확률로 사용한다면 최근 센서 스캔으로 얻은 정보는 최대 우도 추정기에서 한번 사후확률 추정에서 한번 두번 사용더ㅣ어야 합니다. 그리고 로봇은 자신의 자세를 잘못 과신하게 될수 있습니다. 대신 다이클이 닫힐때, 충돌하는 센서 관측에 대한 P($o^{t}$ | $x^{(t)}$, $m^{(t)}$)를 평가하겠습니다. 이러한 과거 관측은 추적 시간과 최대 우도 위치를 유지하여 쉽게 식별할수 있습니다. 그 결과 사후확률 Bel($x^{(t)}$)는 로봇이 탐사되지 않은 공간에 이동하면서 증가하게 됩니다. 이전에 만난 지역과 다시 연결할때 인지 확률 P($o^{t}$ | $x^{(t)}$, $m^{(t)}$)에서의 결과 요소들이 감소하게 될것입니다.
14.4.2 시간 역방향 자세 교정 correcting poses backwards in time
지도 작성의 목표를 고려하면 로봇의 자세 추정치는 사후확률의 Bel($x^{(t)}$)의 모드로 바뀔 것입니다. 다른말로 하자면 14.13을 자세 추정기로 사용하는 대신 사후확률 P($x^{t}$ | $a^{(t-1)}$, $x^{(t-1)}$, m)를 사용하겠습니다. 로봇이 탐사되지 않은 지역으로 이동할 때 $argmax_{x^{(t)}}$ Bel($x^{(t)}$)는 최대 우도 추정기의 근사치와 동일할 것입니다. 하지만 사이클이 닫힐때 두 추정치는 달라질 것입니다.
지도의 일관성을 유지하기위해서 이러한 차이들은 사이클을 따라 시간 역방향으로 전파되어야 합니다. 이것은 다시 중첩 최대 우도 문제가 됩니다. 하지만 계산 효율성도 고려하여야합니다. 역방향 교정을 효율적으로 구현하기 위한 방법으로 다음의 두 페이즈 알고리즘이 있습니다.
1. 단계별 최대 우도 추정치와 사후 확률의 모드 사이의 차이는 사이클을 따라 모든 자세에 대해 선형적으로 분포합니다. 이 선형 수정 항을 계산하는것은 매우 빠르고 교정된 추정치로 닫혀야하는 곳에 위치하게 됩니다. 하지만 최적화 문제는 매우 비선형 적입니다.
2. 이후 증분 최대 우도 추정기는 시간에 대해 역방향으로 이웃이 주어질때 자세의 확률을 최대화 하도록 적용되어 집니다. 이 알고리즘은 위에서 보았던것과 비슷하나 여기서 자세하게 설명하지는 않겠습니다.

표 14.5 사이클이 존재하는 환경에서 지도 작성을 위한 증분 최대 우도 지도작성 알고리즘의 확장판
- 이 알고리즘은 단계별 최대 우도 지도를 따라 자세의 사후확률 추정치를 전달합니다.
- 사이클이 닫힐때 최대우도 추정치 s'와 사후확률의 모드 s''는 달라지고, 로봇 자세의 역방향 조정이 시작됩니다.
표 14.5는 자세에 대한 최대 우도 지도와 완전 사후확률 추정치를 동시에 유지하는 결과 알고리즘을 보여주고 있습니다. 사이클이 닫힐때 최대 우도 자세 추정과 사후확률의 모드는 달라지게 되고, 이 알고리즘의 5번째에서 감지됩니다. 6, 7번째 단계에서 시간 역방향으로 자세 교정 매카니즘이 수행 됩니다.
14.4.3 설명
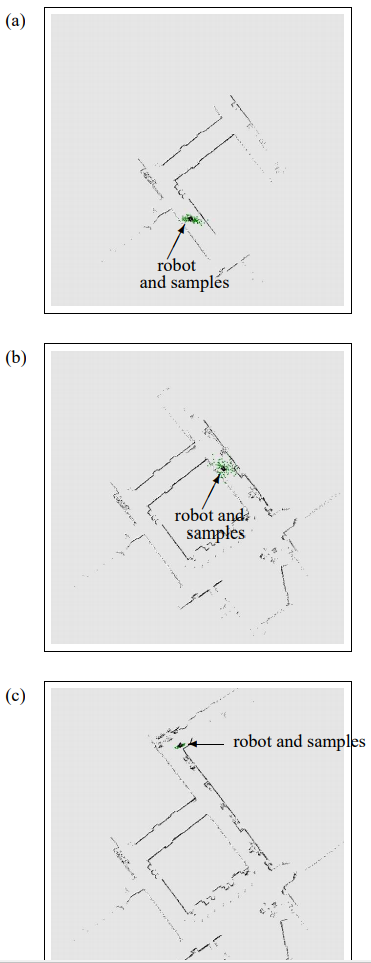
그림 14.3 사후 확률 자세 추정을 위해 파티클 필터를 사용하여 사이클 환경에서 지도 작성
- 로봇을 중심으로하는 주위 점들은 시간에 따라 증가하는 사후확률 신뢰도를 의미합니다.
- 그림 (c)에서 사이클이 닫힐때, 이 지도는 고쳐져서 사후확률은 다시 작아지게 됩니다.
그림 14.3은 그림 14.2에서 본 지도를 생성하기 위해 같은 데이터들을 이 알고리즘에 적용한 예시를 보여주고 있습니다. 여기서 사후확률 추정기는 몬테카를로 위치 추정기 MCL로 구현하였습니다. 시작시 로봇은 모르는 지역에서 시작하여 샘플 집합은 퍼지게 됩니다. 이것은 로봇의 동작 모델처럼 아저 멀리 퍼지지는 않습니다. 그림 14.3a에서는 증분 최대 우도 추정기로 얻은 지도를 따라 사후확률 샘플들을 보여주고 있습니다.
그림 14.3b는 사이클이 닫히기 전 상황을 보여주고 있는데, 이 전에 로봇은 최대 우도 추정기에서 자세추정 오차가 크게 누적되고 있습니다. 하지만 이 에러는 자세의 사후 확률 추정을 파티클 셋으로 잘 잡혀져 왔습니다. 그림 14.3c는 사이클이 닫힌 후 상황을 보여주는데, 지도의 시작 부분과 관측치들이 합해지기 때문에 사후확률 추정치들이 매우 주목받고 있습니다.
최대 우도 추정기를 사용함에도 불구하고 사이클을 위한 증분 최대 우도 지도 작성 incremental ML mapping for cycle 알고리즘은 매우 강인합니다.
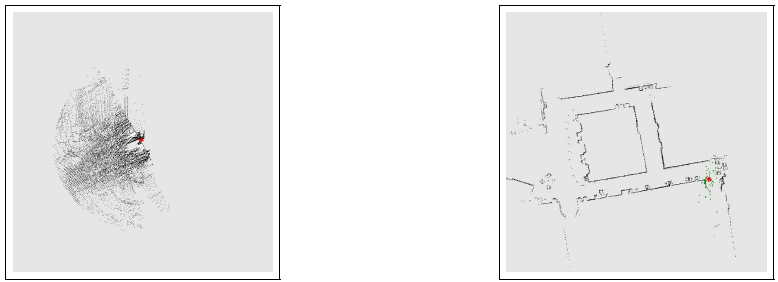
그림 14.4 오도메트리 없이 지도작성
- 좌측은 처리하지 않은 데이터
- 실시간으로 생성된 지도
그림 14.4는 오도메트리 데이터가 주어지지 않는 경우 지도 작성시에 이 알고리즘을 적용한 결과를 보여주고 있습니다. 결과적으로 로 데이터는 해석하기 매우 힘듭니다. 그림 14.4a는 오도메트리 정보의 부재로 인한 데이터 집합을 보여주는데 스캔들의 겹침으로 인해 사람의 눈으로 이해할수 없는 이미지가 나오게 됩니다.
우리가 구한 알고리즘을 이 데이터셋에 적용하면 그림 14.4b처럼 그래도 정확한 지도가 나오게 됩니다. 여기서 기본 알고리즘과 차이는 기울기 $\Delta_{s'}$ log P(s' | a , s)를 생략한 것으로 이것은 동작 a가 존재하지 않으므로 0으로 만들기 위해 생략하였습니다.
지도작성을 하는동안 누적되는 에러는 오도매트리 정보 만큼 크게 근사화됩니다. 하지만 사이클이 닫히면서 루프를 따라 존재하던 에러는 크게 감소하고 결과 지도는 오도메트리 정보가 주어지는 경우와 동일한 퀄리티를 가지게 됩니다. 하지만 이런 결과는ㄴ 소금 한알과 같은데, 이 방법은 레이저 스캐너 데이터로부터 자세를 추정할만큼 충분한 구조적 특성이 없는 특징없는 복도의 경우 실패하게 됩니다. 그렇지만 이 결과들은 일반적인 경우에 강인함을 보여주고 있습니다.
위에서 구한 모든 지도들은 300Mhz 팬티엄 2와 초당 60cm 이동하는 로봇으로 실시간으로 작성하였습니다. 하지만 우리가 알아야 할 것은 이러한 방법들은 중첩된 루프에서 사용할수 없고, 루프가 매우 크다면 실시간으로 사이클을 딸 ㅏ자세 추정치를 고치기는 힘들수도 있습니다.
'로봇 > 로봇' 카테고리의 다른 글
| 파이썬 로보틱스 - 위치추정, 히스토그램 필터 (0) | 2020.07.04 |
|---|---|
| 14.6~ 3차원 지도 작성 (0) | 2020.06.29 |
| 확률적 로봇 공학 - 7.6 대응관계 추정 (0) | 2020.06.24 |
| 파이썬 로보틱스 - 위치추정, 파티클 필터 (0) | 2020.06.20 |
| 칼만, 베이즈 필터 - 파티클 필터 개요와 몬테카를로 방법 (0) | 2020.06.20 |