728x90
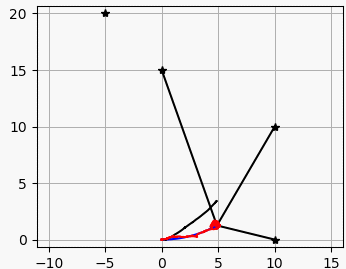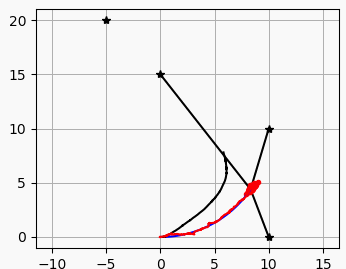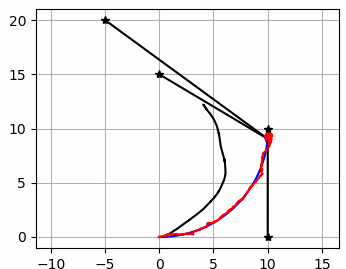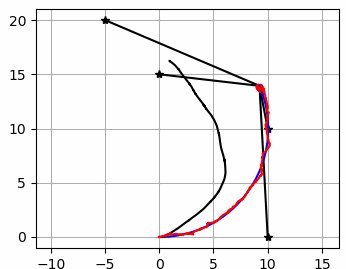
여기서는 파티클필터를 이용한 센서퓨전 위치 추정방법으로
파란 선은 실제 궤적
검은 선은 추측 항법으로 계산한 궤적
빨간선은 파티클 필터로 추정한 궤적입니다.
검은 점은 RFID 랜드마크로 로봇은 랜드마크까지의 거리를 측정하여 파티클 필터 위치추정에 사용합니다.
"""
Particle Filter localization sample
author: Atsushi Sakai (@Atsushi_twi)
"""
import math
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as Rot
# Estimation parameter of PF
Q = np.diag([0.2]) ** 2 # range error
R = np.diag([2.0, np.deg2rad(40.0)]) ** 2 # input error
# Simulation parameter
Q_sim = np.diag([0.2]) ** 2
R_sim = np.diag([1.0, np.deg2rad(30.0)]) ** 2
DT = 0.1 # time tick [s]
SIM_TIME = 20.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range
# Particle filter parameter
NP = 100 # Number of Particle
NTh = NP / 2.0 # Number of particle for re-sampling
show_animation = True
def calc_input():
v = 1.0 # [m/s]
yaw_rate = 0.1 # [rad/s]
u = np.array([[v, yaw_rate]]).T
return u
def observation(x_true, xd, u, rf_id):
x_true = motion_model(x_true, u)
# add noise to gps x-y
z = np.zeros((0, 3))
for i in range(len(rf_id[:, 0])):
dx = x_true[0, 0] - rf_id[i, 0]
dy = x_true[1, 0] - rf_id[i, 1]
d = math.hypot(dx, dy)
if d <= MAX_RANGE:
dn = d + np.random.randn() * Q_sim[0, 0] ** 0.5 # add noise
zi = np.array([[dn, rf_id[i, 0], rf_id[i, 1]]])
z = np.vstack((z, zi))
# add noise to input
ud1 = u[0, 0] + np.random.randn() * R_sim[0, 0] ** 0.5
ud2 = u[1, 0] + np.random.randn() * R_sim[1, 1] ** 0.5
ud = np.array([[ud1, ud2]]).T
xd = motion_model(xd, ud)
return x_true, z, xd, ud
def motion_model(x, u):
F = np.array([[1.0, 0, 0, 0],
[0, 1.0, 0, 0],
[0, 0, 1.0, 0],
[0, 0, 0, 0]])
B = np.array([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT],
[1.0, 0.0]])
x = F.dot(x) + B.dot(u)
return x
def gauss_likelihood(x, sigma):
p = 1.0 / math.sqrt(2.0 * math.pi * sigma ** 2) * \
math.exp(-x ** 2 / (2 * sigma ** 2))
return p
def calc_covariance(x_est, px, pw):
"""
calculate covariance matrix
see ipynb doc
"""
cov = np.zeros((3, 3))
n_particle = px.shape[1]
for i in range(n_particle):
dx = (px[:, i:i + 1] - x_est)[0:3]
cov += pw[0, i] * dx @ dx.T
cov *= 1.0 / (1.0 - pw @ pw.T)
return cov
def pf_localization(px, pw, z, u):
"""
Localization with Particle filter
"""
for ip in range(NP):
x = np.array([px[:, ip]]).T
w = pw[0, ip]
# Predict with random input sampling
ud1 = u[0, 0] + np.random.randn() * R[0, 0] ** 0.5
ud2 = u[1, 0] + np.random.randn() * R[1, 1] ** 0.5
ud = np.array([[ud1, ud2]]).T
x = motion_model(x, ud)
# Calc Importance Weight
for i in range(len(z[:, 0])):
dx = x[0, 0] - z[i, 1]
dy = x[1, 0] - z[i, 2]
pre_z = math.hypot(dx, dy)
dz = pre_z - z[i, 0]
w = w * gauss_likelihood(dz, math.sqrt(Q[0, 0]))
px[:, ip] = x[:, 0]
pw[0, ip] = w
pw = pw / pw.sum() # normalize
x_est = px.dot(pw.T)
p_est = calc_covariance(x_est, px, pw)
N_eff = 1.0 / (pw.dot(pw.T))[0, 0] # Effective particle number
if N_eff < NTh:
px, pw = re_sampling(px, pw)
return x_est, p_est, px, pw
def re_sampling(px, pw):
"""
low variance re-sampling
"""
w_cum = np.cumsum(pw)
base = np.arange(0.0, 1.0, 1 / NP)
re_sample_id = base + np.random.uniform(0, 1 / NP)
indexes = []
ind = 0
for ip in range(NP):
while re_sample_id[ip] > w_cum[ind]:
ind += 1
indexes.append(ind)
px = px[:, indexes]
pw = np.zeros((1, NP)) + 1.0 / NP # init weight
return px, pw
def plot_covariance_ellipse(x_est, p_est): # pragma: no cover
p_xy = p_est[0:2, 0:2]
eig_val, eig_vec = np.linalg.eig(p_xy)
if eig_val[0] >= eig_val[1]:
big_ind = 0
small_ind = 1
else:
big_ind = 1
small_ind = 0
t = np.arange(0, 2 * math.pi + 0.1, 0.1)
# eig_val[big_ind] or eiq_val[small_ind] were occasionally negative
# numbers extremely close to 0 (~10^-20), catch these cases and set the
# respective variable to 0
try:
a = math.sqrt(eig_val[big_ind])
except ValueError:
a = 0
try:
b = math.sqrt(eig_val[small_ind])
except ValueError:
b = 0
x = [a * math.cos(it) for it in t]
y = [b * math.sin(it) for it in t]
angle = math.atan2(eig_vec[big_ind, 1], eig_vec[big_ind, 0])
rot = Rot.from_euler('z', angle).as_matrix()[0:2, 0:2]
fx = rot.dot(np.array([[x, y]]))
px = np.array(fx[0, :] + x_est[0, 0]).flatten()
py = np.array(fx[1, :] + x_est[1, 0]).flatten()
plt.plot(px, py, "--r")
def main():
time = 0.0
# RF_ID positions [x, y]
rf_id = np.array([[10.0, 0.0],
[10.0, 10.0],
[0.0, 15.0],
[-5.0, 20.0]])
# State Vector [x y yaw v]'
x_est = np.zeros((4, 1))
x_true = np.zeros((4, 1))
px = np.zeros((4, NP)) # Particle store
pw = np.zeros((1, NP)) + 1.0 / NP # Particle weight
x_dr = np.zeros((4, 1)) # Dead reckoning
# history
h_x_est = x_est
h_x_true = x_true
h_x_dr = x_true
while SIM_TIME >= time:
time += DT
u = calc_input()
x_true, z, x_dr, ud = observation(x_true, x_dr, u, rf_id)
x_est, PEst, px, pw = pf_localization(px, pw, z, ud)
# store data history
h_x_est = np.hstack((h_x_est, x_est))
h_x_dr = np.hstack((h_x_dr, x_dr))
h_x_true = np.hstack((h_x_true, x_true))
if show_animation:
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
for i in range(len(z[:, 0])):
plt.plot([x_true[0, 0], z[i, 1]], [x_true[1, 0], z[i, 2]], "-k")
plt.plot(rf_id[:, 0], rf_id[:, 1], "*k")
plt.plot(px[0, :], px[1, :], ".r")
plt.plot(np.array(h_x_true[0, :]).flatten(),
np.array(h_x_true[1, :]).flatten(), "-b")
plt.plot(np.array(h_x_dr[0, :]).flatten(),
np.array(h_x_dr[1, :]).flatten(), "-k")
plt.plot(np.array(h_x_est[0, :]).flatten(),
np.array(h_x_est[1, :]).flatten(), "-r")
plot_covariance_ellipse(x_est, PEst)
plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
if __name__ == '__main__':
main()300x250
'로봇 > 로봇' 카테고리의 다른 글
| 14.4 증분 지도작성과 사후확률추정 (0) | 2020.06.29 |
|---|---|
| 확률적 로봇 공학 - 7.6 대응관계 추정 (0) | 2020.06.24 |
| 칼만, 베이즈 필터 - 파티클 필터 개요와 몬테카를로 방법 (0) | 2020.06.20 |
| 파이썬 로보틱스 - 위치추정, 확장 칼만 필터 (0) | 2020.06.20 |
| 칼만과 베이즈 필터 in python (0) | 2020.06.19 |