대표적인 분류 문제로 피마 인디언 당뇨병 여부를 예측(분류)를 해보자
링크는 www.kaggle.com/uciml/pima-indians-diabetes-database
잠깐 소개 문구를 읽어보면
당뇨병, 소화, 신장 질환 등을 연구하는 국립 연구소에서 얻은 데이터고
이 데이터셋으로 우리가 할일은 환자가 당뇨병을 가지고 있는지 예측하면 된다.
내용물은 여러개의 독립변수와 한개의 목표 변수(Outcome)
독립 변수는 환자의 임신 횟수, BMI, 인슐린, 나이 등이 있다고 한다.

우리가 할일은 뭐더라
일단 이 문제가 당뇨병 여부인지를 판단하는 것이므로
분류 문제임을 알았다.
머신러닝 알고리즘을 활용하는 과정은
0. 데이터 훑어보기
1. 탐색적 데이터 분석
2. 전처리
3. 모델 학습
4. 성능 평가
정도로 분류할수 있을거 같구.
지금까지 학습한 내용들을 전부 활용해서 해보면
탐색적 데이터 분석에서는
시본으로 페어플롯이나 다양한 플롯들을 그리면서 분석할 예정
전처리 단계에서는
결측치 처리, 라벨 인코딩, 열 드롭 등 할거고
모델 학습 단계에서는
분류기 모델들 설정,
gridsearchcv로 하이퍼 파라미터별 최적 추정기를 구하고자 한다.
성능 평가 단계에서는 조금전에 확인한
성능 평가지표들을 구하여 비교해보자
0. 빠르게 훑어보기
- 평소 하던데로 기본 라이브러리 임포트와 데이터 프레임 조회
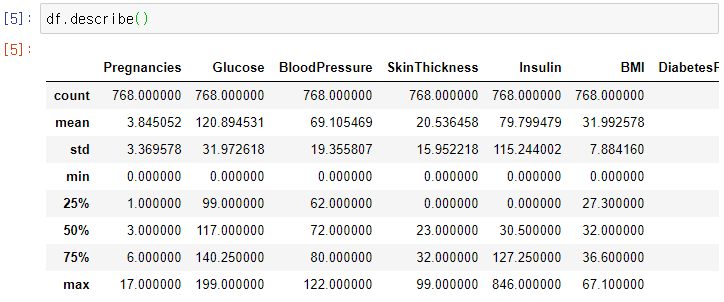
- 기초 통계량, 데이터 형태 등을 확인해봄.
* 위 설명대로 당뇨병 여부인 목표변수 Outcome과 이를 설명하기 위한 Pregenancies, BMI, Insulin 등이 있다.
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
df = pd.read_csv("res/pima/diabetes.csv")
df.info()

1. 탐색적 데이터 분석
- 데이터를 전처리 하기에 앞서 데이터간 의미를 한번 살펴보고자 한다.
- 우선 데이터나 변수도 많지 않고, 편하게 seaborn의 pairplot을 사용해보자.
* 사진이 잘 안보이므로 따로 다운로드 받아서 확대해서 보면 수월하다.
- 회귀 문제가 아니다 보니 출력 변수와 타 변수간의 상관관계를 알아보기가 힘들다.
sns.pairplot(df)
- 회귀 문제가 아니다 보니 출력 변수와 타 변수간의 상관관계를 알아는데는 pairplot은 좋지 않아보인다.

- 한번 임신 횟수에 대한 박스 플롯을 보자
-> 평균 임신 횟수가 약 3회 정도가 되나 13회를 넘어가는 아웃라이어들이 존재한다.
-> 한개의 박스 플롯으로 의미있는 정보를 보기 힘드니 여러개를 띄워보자
sns.boxplot(y="Pregnancies", data=df)
- 당뇨병 여부에 따른 임신 횟수를 살펴봣더니, 임신 횟수가 적을 수록 당뇨병 발병이 적은걸 알수 있다.
sns.boxplot(x="Outcome", y="Pregnancies", data=df)
- 나머지 변수들도 비슷한 결과를 보이고 있다.


- 나이대별 발병 여부는 어떨까?
-> 젊은 층보다 중고령층인 경우 발병확률이 높음을 알 수 있다.
plt.figure(figsize=(12,6))
sns.barplot(x="Age", y="Outcome", data=df)
- 임신 횟수별 발병율을 바 플롯으로 본 결과. 횟수가 많을수록 유병율이 높은걸 확인할수 있다.
plt.figure(figsize=(12,6))
sns.barplot(x="Pregnancies", y="Outcome", data=df)
대강 탐색적 데이터 분석은 여기까지 하고
2. 전처리
이제 전처리 과정을 생각해보려고 한다.
전처리 과정에서 할일은 이렇게 정리할수 있을것같다.
1. 결측치 처리
2. 데이터 분할
3. 인코딩
4. 스케일링/정규화
5. 아웃라이어 처리
2. 1 우선 결측치 부터 처리하자
- 전처리 단계서 사용할 라이브러리 임포트
- 결측치를 확인해보니 존재하지 않는다.
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
df.isnull().sum()
2.2 아웃라이어 처리
- 데이터프레임의 기초 통계량들을 보자
- 값 > 평균 + 3 * 표준편차들은 아웃라이어로 보고 좀 생각해보자

- 전체 768 행 데이터 중에서 아웃라이어들 갯수를 다 합쳐도 40개쯤 되는거 같다.
-> 이 아웃라이어가 존재하는 행들은 다 제거해주자.
cols = df.columns
print(df.shape)
for col in cols:
mean = df[col].mean()
std = df[col].std()
threshold = mean + 3 * std
n_outlier = np.sum(df[col] > threshold)
print(col + ". num of outlier : "+str(n_outlier))
- 위 조건을 넘는 값을 아웃라이어로 판단하고, 제거하였다.
-> 제거한 결과 768개 에서 727개로 줄어듦. 이제 스케일링 처리를 수행하자.
cols = df.columns
print("before drop outlier : {}".format(df.shape))
for col in cols:
mean = df[col].mean()
std = df[col].std()
threshold = mean + 3 * std
n_outlier = np.sum(df[col] > threshold)
#print(df[df[col] > threshold])
df.drop(df[df[col] > threshold].index[:], inplace=True)
df.dropna()
print("after drop outlier : {}".format(df.shape))
2.3 피처 스케일링
- 가우시안 커널을 사용하는 머신러닝 기법들은 특징들이 가우시안 분포를 따르는 경우 잘 동작된다고 한다.
- 모든 피쳐 데이터들을 표준화 시켜주기 위해 Standard Scaler를 사용해보자
-> 모든 데이터들이 표준 정규분포를 따르는 값들로 변환이 되었다.
X = df.loc[:, df.columns != "Outcome"]
y = df.loc[:, df.columns == "Outcome"]
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(X_scaled[:,:6])
3. 모델링
결측치는 없고,
아웃라이어 제거했고,
스케일링도했고,
라벨링 할 값도 존재하지 않는다.
이제 전처리 과정은 끝났으니 모델 구성, 학습을 해보자
내가 사용할 분류기는
1. Logistic Regression
2. SVM
3. Decision Tree
4. Random Forest
이 내가지를 사용하고자 한다.
여기서 grid seacrh cv를 사용하고자 하는데 사용할 파라미터들을 정리해야한다.
다큐먼트를 참고하여 설정할 파라미터들
1. Logistic Regression
-> penalty : "l1", "l2", "elasticnet", "none" default "l2"
2. SVM.svc
-> kernel{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’}, default=’rbf’
3. Decision Tree
4. Random Forest
트리는 max_depth와 min_samples_split을 사용하자.
하이퍼 파라미터에 따른 각 분류기들별 최적 성능과 최적의 파라미터를 구한 결과
대부분 비슷비슷하나
로지스틱 회귀에서 0.7917로 가장 좋은 성능이 나왔다.

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
def fit_clasifiers(gs_clfs, X, y):
for clf in gs_clfs:
print(X.shape)
clf.fit(X, y)
def show_gridsearch_result(gs_clfs):
estimators = []
scores = []
params = []
for clf in gs_clfs:
estimators.append(str(clf.estimator))
scores.append(clf.best_score_)
params.append(clf.best_params_)
for i, val in enumerate(estimators):
print(val)
print(scores[i])
print(params[i])
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2)
lr = LogisticRegression()
svc = SVC(probability=True)
dt = DecisionTreeClassifier()
rf = RandomForestClassifier()
param_lr = {"penalty":["l1", "l2", "elasticnet", "none"]}
param_svc = {"kernel":["linear", "poly", "rbf", "sigmoid"]}
param_tree = {
"max_depth" : [3, 4, 5, 6],
"min_samples_split" : [2, 3]
}
gs_lr = GridSearchCV(lr, param_grid=param_lr, cv=5, refit=True)
gs_svc = GridSearchCV(svc, param_grid=param_svc, cv=5, refit=True)
gs_dt = GridSearchCV(dt, param_grid=param_tree, cv=5, refit=True)
gs_rf = GridSearchCV(rf, param_grid=param_tree, cv=5, refit=True)
gs_clfs = [gs_lr, gs_svc, gs_dt, gs_rf]
fit_clasifiers(gs_clfs, X_train, y_train)
show_gridsearch_result(gs_clfs)
5. 평가지표들 살펴보기
- l2 패널티를 준 로지스틱 회귀 모델에서
- 혼동 행렬, 정확도, 재현률, 정밀도, roc curve와 roc_auc score 등을 살펴보자
- 정확도는 77.39, 정밀도는 0.8이나 재현율이 0.56으로 크게 떨어지고 있다.
- 임계치 0.3 부근에서 교차하므로 이지점을 기준으로 분류가 필요해보인다.

from sklearn.metrics import accuracy_score, confusion_matrix, roc_auc_score
from sklearn.metrics import recall_score, precision_score,roc_curve
from sklearn.metrics import precision_recall_curve
def show_metrics(y_test, y_pred):
confusion = confusion_matrix(y_test, y_pred)
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
print(confusion)
print("Acc : {}".format(accuracy))
print("precision : {}".format(precision))
print("recall : {}".format(recall))
def show_precision_recall_curve(y_test,prob_positive_pred):
precisions, recalls, thresholds = precision_recall_curve(y_test, prob_positive_pred)
print("th val : {}".format(thresholds[:4]))
print("precision val : {}".format(precisions[:4]))
print("recalls val : {}".format(recalls[:4]))
df = {
"thresholds":thresholds,
"precisions":precisions[:-1],
"recalls":recalls[:-1]
}
df = pd.DataFrame.from_dict(df)
sns.lineplot(x="thresholds", y="precisions", data=df)
sns.lineplot(x="thresholds", y="recalls", data=df)
y_pred = gs_lr.predict(X_test)
pred_prob = gs_lr.predict_proba(X_test)
show_metrics(y_test, y_pred)
y_pred = np.concatenate([pred_prob, y_pred.reshape(-1, 1)], axis=1)
prob_positive_pred = y_pred[:, 1]
show_precision_recall_curve(y_test,prob_positive_pred)
- roc cuv
-> roc_auc 값은 0.8188

def show_roc_curve(y_test,prob_positive_pred):
fpr, tpr, thresholds = roc_curve(y_test,prob_positive_pred)
print("fpr val : {}".format(fpr[:4]))
print("tpr val : {}".format(tpr[:4]))
print("thresholds val : {}".format(thresholds[:4]))
df = {"threshold":thresholds, "fpr":fpr, "tpr":tpr}
df = pd.DataFrame.from_dict(df)
sns.lineplot(x="fpr", y="tpr", data=df)
roc_score = roc_auc_score(y_test, prob_positive_pred)
print(roc_score)
show_roc_curve(y_test,prob_positive_pred)
6. 수정
이 문제를 풀면서 이상하게
정확도가 떨어지는지 보니
아웃라이어 처리때 상한 아웃라이어만 처리하고
하한 아웃라이어들은 처리하지 않았더라
하한 아웃라이어의 값들을 살펴보았다.
6.1 하한 아웃라이어
- 하한 아웃라이어들은 대부분 0으로 나오길래, 실제 값이 0인 데이터들의 갯수를 확인하였다.
- 임신 여부는 0일수도 있으니 넘어가더라도 SkinThickness와 insulin의 0이 너무 많다고 나오고 있다.
=>다른 열의 0행들은 제거하면 되지만, 많은 부분을 차지하는 행은 평균 값을 삽입해주자.


def show_lower_outlier(df, stdev=3, show_total=False):
# lower bound outliers
cols = df.columns
print(df.shape)
for col in cols:
#std
mean = df[col].mean()
std = df[col].std()
threshold = mean - stdev * std
n_outlier = np.sum(df[col] < threshold)
print(col + ". mean : "+str(round(mean,3))+", num of outlier : "+str(n_outlier))
if (show_total == True) & (n_outlier != 0):
print(df.loc[(df[col] < threshold),col][:5])
print(" -> cnt of zero : " + str(np.sum(df[col] == 0))+"\n")
show_lower_outlier(df,show_total=True)
- 인슐린, 피부두께, 혈압에 평균을 대입
df.loc[ df.loc[:, "Insulin"] == 0 , "Insulin"] = df["Insulin"].mean()
df.loc[ df.loc[:, "SkinThickness"] == 0 , "SkinThickness"] = df["SkinThickness"].mean()
df.loc[ df.loc[:, "BloodPressure"] == 0 , "BloodPressure"] = df["SkinThickness"].mean()
show_lower_outlier(df,show_total=True)
- outcome을 제외한 타 컬럼들의 0값은 Nan으로 변환후 제거
-> 768행에서 752행으로 줄었다.
* 그냥 outcome을 진작에 떄놓고 할걸 .. 떗따 붙엿다 힘들다.
print("before drop: "+ str(df.shape))
dfi = df.loc[:, (df.columns != "Outcome") & (df.columns != "Pregnancies")]
dfi[dfi[:] == 0] = np.NaN
dfi = dfi.dropna()
df.iloc[:,:-1] = dfi
show_lower_outlier(df,show_total=True)

너무 이문제에서 삽질 많이 했는데
매번 바뀌긴 하지만 결과를 정리하면
다음 전처리만 한 경우
- 상한 : 평균 + 3 * std 제거
=> acc : 0.753. , ROC AUC = 0.8119


전처리 추가시
- 하한 : 평균 - 3 * std제거, 일부 변수 0값 평균 대입, 0제거
=> ACC = 0.82119, ROC AUC = 0.8947


여러번 실행하면서 결과가 달라지다보니
하한 전처리를 추가했다고 항상 성능이 개선되지는 않았다.
'인공지능' 카테고리의 다른 글
| 파이썬머신러닝 - 9. 결정 트리를 이용한 사용자 행동 인식 분류하기 (0) | 2020.11.25 |
|---|---|
| 파이썬머신러닝 - 8. 결정 트리 (0) | 2020.11.25 |
| 파이썬머신러닝 - 6. 성능 평가 지표 (0) | 2020.11.24 |
| 파이썬머신러닝 - 5. 타이타닉 생존자 예측 (0) | 2020.11.23 |
| 파이썬머신러닝 - 4. 데이터 전처리 : 인코딩/피처 스케일링 (0) | 2020.11.23 |