C4W2L01 Why look at case studies?
- 이번 시간에는 지난 주에 배운 기초 블록들로 만든 신경망 케이스 연구들을 살펴보자.
- 누군가 개발한 개, 고양이 분류 신경망을 자율 주행이나 다른 분야에도 활용 할 수도 있음.
- 다음 강의에서 볼 고전 신경망으로 LeNet-5, Alexnet, VGG 등
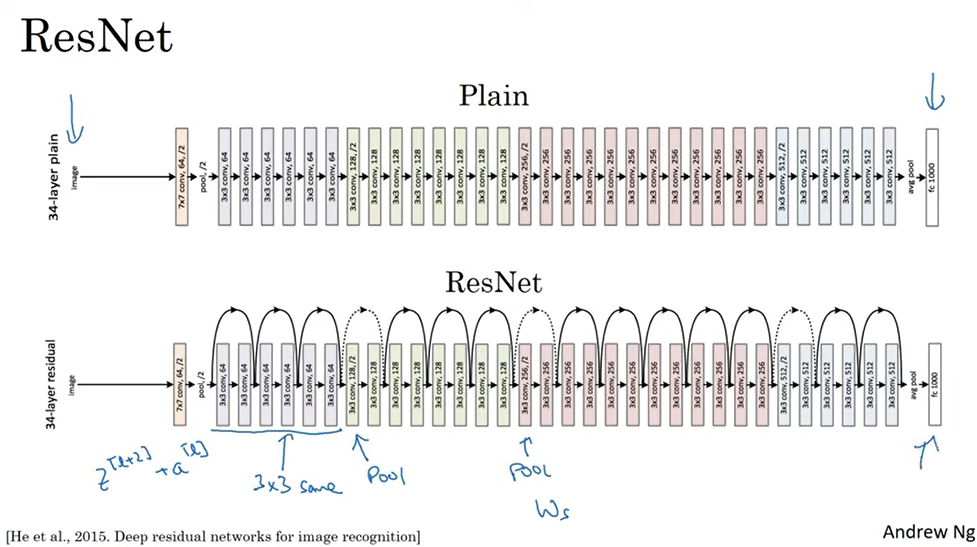
- 그 다음으로 resnet에 대해서 살펴볼것임. resnet은 깊게 학습 가능함.
- 마지막 케이스 스터디로 inception에 대해서 배우자.

C4W2L02 Classic Network
LeNet-5
- LeNet-5는 32 x 32 x 1 크기의 흑백 손글씨 이미지를 인식하는 모델
- conv2d, 5 x 5, s=1, 필터 6개 사용, no padding => 28 x 28 x 6
- avg pooling, f = 2, s = 2 => 14 x 14 x 6
- conv2d, 5 x 5, s = 1, 16 filters, no padding => 10 x 10 x 16
- avg pooling, f=2, s=2 => 5 x 5 x 16 = 400
- flatten 후 fully connected layer, hidden unit 120
- fc2, 84 => y_hat, 10 categories, softmax
- 60k parameter로 작은편, 요즘은 10m, 100M등 수천배만음.
- N_h, N_w가 줄어들고, N_c가 늘어남.
- conv - pool -> conv - pool -> fc -> fc -> output
- tahn/sigmoid를 활성화 함수로 사용하고, 당시에는 relu는 잘 안씀 * 풀링 뒤에 비선형 활성화 함수 사용.
* 이 논문을 읽을때 섹션 2, 3 읽기를 추천함.

AlexNet
- Alex krizhesky et al.
- 227 x 227 x 3 크기 이미지를 사용.
- 1. 11 x 11, s = 4, N_c = 96 => 55 x 55 x 96, max pooling 3 x 3, s= 2 => 27 x 27 x 96
- 2. 5 x 5, same, N_c = 256 => 27 x 27 x 256, max pooling 3 x 3, s = 2 => 13 x 13 x 256
- 3. conv + max_pooling => 6 x 6 x 256 = 9216
- 4. fc 4096 -> fc 1000 -> softmax, 1000
- LeNet-5와 유사하나 훨씬 큼. (LeNet - 60k 개의 파라미터였다면, AlexNet은 60M개의 파라미터를 가짐)
- LeNet-5와 달리 ReLU를 활성화 함수를 사용.
- 당시 GPU 성능이 나빠 두 개의 GPU에서 작업하도록 나눠서 사용.
- Local Response Normalization layer 도 있었으나 자주 사용되지 않음.
* 13 x 13 x 256 LRN은 h,w 한지점의 모든 채널을 보고 정규화 수행. 높은 활성 값을 가진 경우가 많아지는걸 방지하기 위함. 성능 상 유용하지는 않았음.

VGG - 16
- 단순한 신경망으로 간결함이 장점. conv = 3 x 3 filter, s = 1, same, max pool = 2 x 2, s = 2
- 1. 224 x 224 x 3 -> (conv 64) x 2-> 224 x 224 x 64 -> (max pooling) -> 112 x 112 x 64
- 2. 112 x 112 x 64 -> (conv 128) x 2 -> (max pooling) -> 56 x 56 x 128 => (여러번 반복)
- 3. 7 x 7 x 512 ->. (fc 4096) -> (fc 4096) -> softmax, 1000
- vgg-16인 이유는 16개의 레이어/층을 가지기 때문
- 138M 파라미터로 상당히 크나, 일관적임
- 다음 단계로 넘어갈때마다 필터 갯수가 규칙적으로 2배가 됨.
- 더 큰 버전으로 VGG - 19도 있음.