B. 3차원 레이저기반 지도작성
3차원으로 SLAM 알고리즘을 확장하는것에 대해서 이전 색션에서 살펴보았습니다. 차이는 2차원 스캔 매치와 루프 클로저 검출을 3차원 포인트 클라우드에서 동작하는 3차원 알고리즘들로 대체하면 됩니다. 구현하기 위해서 유명한 ICP 알고리즘을 사용하였고, Steder가 제안한 알고리즘으로 루프 클로저를 검출하였습니다. 게다가 그래프의 각 노드와 각 제약들은 SE(3)에서 존재합니다. 이 알고리즘의 결과는 그림 2(a)와 (b)가됩니다.
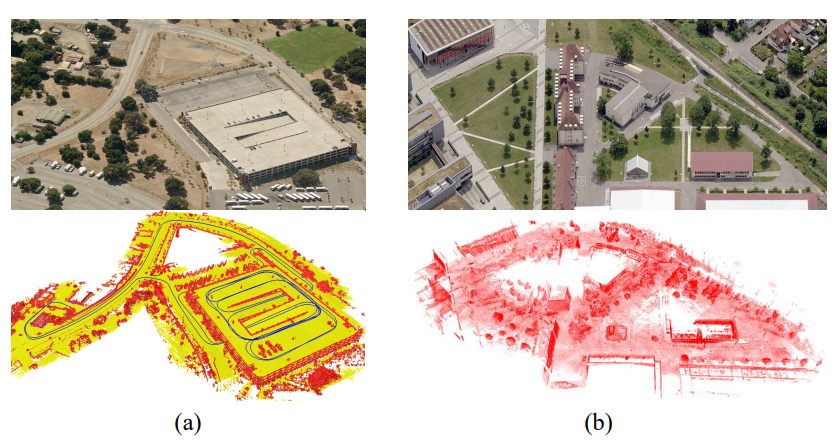
그림 2. 그래프 기반 3차원 지도작성 결과
SE(3)의 요소를 나타내기 위한 파라미터의 최소 갯수는 6개로 3차원 평행이동 백터와 3차원 오일러각으로 구성됩니다. 이 파라미터화를 사용하여 알고리즘 1을 얻을수 있습니다. 하지만 이 최소화 표현은 특이해지도작성
3차원으로 SLAM 알고리즘을 확장하는것에 대해서 이전 색션에서 살펴보았습니다. 차이는 2차원 스캔 매치와 루프 클로저 검출을 3차원 포인트 클라우드에서 동작하는 3차원 알고리즘들로 대체하면 됩니다. 구현하기 위해서 유명한 ICP 알고리즘을 사용하였고, Steder가 제안한 알고리즘으로 루프 클로저를 검출하였습니다. 게다가 그래프의 각 노드와 각 제약들은 SE(3)에서 존재합니다. 이 알고리즘의 결과는 그림 2(a)와 (b)가됩니다.
SE(3)의 요소를 나타내기 위한 파라미터의 최소 갯수는 6개로 3차원 평행이동 백터와 3차원 오일러각으로 구성됩니다. 이 파라미터화를 사용하여 알고리즘 1을 얻을수 있습니다. 하지만 이 최소화 표현법은 특이해를 가지며, 과 파라미터화된 상태공간을 사용하여 피할수 있습니다.
대안으로 최소 표현법에서는 자세에서 벗어날때 최적화 문제의 상대적인 작은 변화를 $\Deta \breve{x}$로 나타낼수 있습니다. 이를 통해 알고리즘 2를 구할수가 있게 됩니다. 이번 장에서는 시뮬레이션된 로봇 얻은 자세 그래프에 두갖 ㅣ최적화 알고리즘들을 비교하여보겠습니다.
해시안의 희소 패턴은 두 케이스다 같으며, 선형 시스템을 계싼하는 시간은 무시하겠습니다. 파라미터화의 선택에 따라 수렴 속도에 영향을 주며, 한번 반복하는데 필요한 시간에는 영향을 주지는 않습니다. 이 효과를 강조하기 위해서 두 알고리즘을 사용하여 한번 최적화가 수행되는 동안 반복당 에러 변화를 보여주겠습니다.

그림 11. 구에서 주행한 시뮬레이션된 로봇으로 얻은 자세-그래프
좌측 : 초기 형태, 우측 : 자세-그래프를 최적화 한후 결과로 알고리즘 2로 정밀하게 복원되었습니다.
이 실험에서는 구 표면을 주행하는 로봇의 시뮬레이션된 3차원 데이터 셋을 사용하겠습니다. 측정치는 에러의 영향을 받고 있으며, 오도메트리 정보로 초기한 경우에 그림 11의 왼쪽 그림과 같은 그래프가 만들어 졌습니다. 초기 추측에서부터 시작하여, 가우스-뉴턴 알고리즘에 매니폴드 선형화를 적용한 경우나 적용하지 않은 상태(오일러 각 사용)로 실행하였습니다.

그림.12 3차원 구 데이터셋에 오일러각을 사용한 경우와 매니폴드 선형화를 사용하여 가우스-뉴턴 최적화로 얻은 오차 F(x)의 변화
그림 12는 두 방법으로 반복하는 동안 오차의 변화를 보여주고 있습니다. 처음에는 두 방법다 에러가 줄어들고 있었으나, 특이해가 알고리즘1이 발산하도록 하며, 알고리즘 2는 올바른 해를 향해 수렴하도록 하고 있습니다.
6. 결론
본 튜토리얼에서는 그래프 기반 SLAM에 대해서 소개하였습니다. 이 자료의 목적은 독자들이 제안된 방법을 쉽게 구현하고 세부적인 내용들을 효과적으로 전달하기 위함이고, 이 자료에서 소개한 알고리즘은 더복잡한 방법으로 블록을 만들어 사용해도 됩니다. 하지만 이 알고리즘을 최적화하여 구현하는것은 상당히 힘든 문제가 됩니다.
'로봇 > SLAM' 카테고리의 다른 글
| 5 Minutes with Cyrill - 0. 소개 (0) | 2020.08.25 |
|---|---|
| 그래프 기반 SLAM 튜토리얼 - 5. 응용 (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 4.C 매니폴드에서 최소 제곱 (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 4.B 선형화된 시스템의 구조에 대한 고려사항들 (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 4.A 지역 선형화 반복을 통한 에러 최소화 (0) | 2020.07.08 |