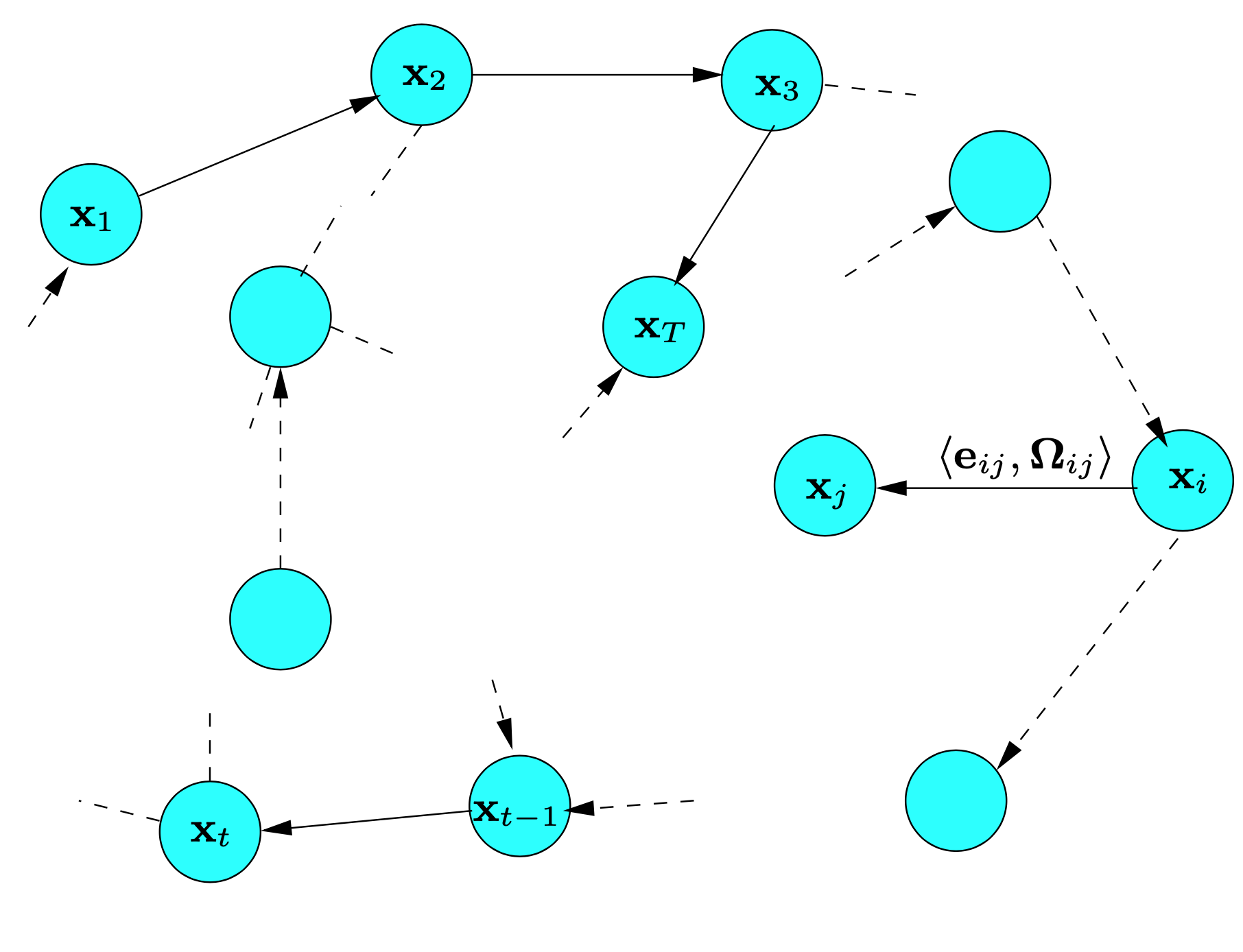
그림 6. SLAM 과정의 자세 그래프 표현. 그래프 상의 모든 노드들은 로봇의 자세를 의미합니다. 가까운 자세들끼리는 에지로 연결되어 있으며, 이 에지는 로봇의 자세 사이에서 관측으로 생기는 공간적인 제약들을 나타냅니다. 에지 $e_{t-1 t}$는 연속적인 자세들 사이에 있으며, 오도메트리 측정치를 설계하며, 다른 에지들은 동일하 환경에서 다중 관측으로부터 만들어지는 공간적인 제약조건들을 의미합니다.
x = ($x_1$, . . ., $x_T$$)^T$는 자세 노드 $x_i$의 벡터이며, $z_{ij}$와 $\Omega_{ij}$는 노드 i와 노드 j사이 가상 측정의 평균과 정보행렬을 의미합니다. 이 가상 측정은 i로부터 얻은 관측들이 j에서 얻은 관측들로 포개도록 만드는 변환입니다. 노드 $x_i$와 $x_j$의 형태가 주어질때 가상 측정의 예측치를 $\hat{z_{ij}}$($x_i$, $x_j$)라고 합시다.
이 예측은 두 노드 사이에 상대적인 변환이라고 할수 있으며, 관측 $z_{ij}$의 로그 우도 $l_{ij}$는 그러므로 다음과 같습니다.

e($x_i$, $x_j$, $z_{ij}$)는 기대 관측 $\hat{z_{ij}}$($x_i$, $x_j$)과 실제 관측 $z_{ij}$ 사이의 차이를 계산하는 함수로, 이 표기를 간단하게 정리하자면 관측 인덱스들을 에러 함수의 인덱스들로 바꾸겠습니다.


그림 7. 정점 $x_i$와 $x_j$를 연결하는 에지의 측면들. 이 에지는 관측 $z_{ij}$에서 시작합니다. 두 노드사이의 상대적인 차이로부터, $x_i$ 좌표계에서 보여지는 $x_j$를 나타내는 기대 측정치 $\hat{z_{ij}}$를 계산할수 있습니다. 에러 $e_{ij}$($x_i$, $x_j$)는 기대와 실제 측정치 사이의 차이에 의존하게되며, 에지는 에러 함수 $e_{ij}$($x_i$, $x_j$)와 불확실성을 나타내는 측정의 정보 행렬 $\Omega_{ij}$로 정리할수 있겠습니다.
그림 7은 그래프의 에지를 정의하는 양과 함수들을 보여주고 있습니다. C는 관측 제약 z가 존재하는 쌍 인덱스들의 집합이며, 최대 우도 방법의 목표는 모든 관측들에 대해 음의 로그 우도 F(X)를 최소화하는 노드 $x^{*}$의 형태를 찾는것이 되겠습니다.

이를 정리하면, 다음의 식을 푸는문제라고 할수 있겠습니다.

이번 섹션에서는 식 (5)를 풀고, 로봇의 주행 궤적에 따른 가우시안 근사를 계산하는 방법에 대해 설명하겠습니다. 가우스-뉴턴이나 Levenberg-Marquardt 알고리즘 같은 기존 최적화 방법을 사용하는 방법도 있지만, 이 방법은 구조 문제로 다루기 때문에 특히나 효율적으로 동작하게 됩니다.
우선 기존의 비선형 최소제곱 최적화 구현을 설명하고, 다음에는 로봇 자세 표현의 특이성을 다룰수 있도록 도와주는 다른 방법들을 소개하겠습니다.
A. 지역 선형화 반복을 통한 에러 최소화
로봇의 자세에 대한 좋은 초기 추측 guess $\breve{x}$를 알고있다면, 식 (5)의 수치적인 해는 가우스-뉴턴 법이나 Levenberg-Marquardt 알고리즘을 사용하여 얻을수 있겠습니다. 이 아이디어는 현재 초기 추측 $\breve{x}$ 주위에 1차 태일러 전개로 에러 함수를 근사화하는것으로 다음과 같습니다.

여기서 $J_{ij}$는 $\breve{x}$와 $e_ij$ = $e_{ij}$($\breve{x}$)로 계산되는 $e_{ij}$(x)의 자코비안입니다. 식 (4)의 에러 항 $F_{ij}$에 식 (7)을 대입하면 다음의 식을 얻을수 있겠습니다.

식 (14)와 같은 이차 식은 식 (13)에서 c = $\Sigma$$c_{ij}$, b = $\Sigma$$b_{ij}$, 그리고 H = $\Sigma$$H_{ij}$로 설정하여 얻을수 있으며, 선형 시스템의 해를 구함으로서 $\Delta$를 최소화 시킬수 있겠습니다.

행렬 H는 자코비안을 통해 궤정의 상태 공간에서 관측 에러를 사영함으로서 얻을수 있기 때문에 H는 시스템의 정보 행렬이 됩니다. 제약 조건에 의해 연결되는 자세들 사이에는 0이 아닌 값들을 가지며, 희소한 행렬이 됩니다. 이 행렬은 희소 Cholesky 분해를 이용하여 식 (15)을 풀수 있도록 도와줍니다. 희소 Cholesky 분해를 효과적으로 구현하기 위해 CSparse라이브러리를 사용할수 있겠습니다.
초기 추정을 더함으로서 선형화된 해률 얻을수 있게됩니다.

많이 사용되는 가우스-뉴턴 알고리즘은 식 (14)의 선형화와 식 (15)의 해, 식 (16)에서 갱신 단계를 반복해서 수행합니다. 모든 반복과정에서 이전의 해가 선형화 지점과 초기 추정치로 사용됩니다.
위에서 설명한 과정들은 다변수 함수 최소화에 사용하는 일반적인 방법으로 SLAM 문제의 특별한 경우에서 사용됩니다. 하지만 이 일반적인 방법은 파라미터 x들의 공간이 유클리디안이라고 가정하고 있으며, 이 경우에는 SLAM에 사용할수 없으며, 하부 최적의 해를 구해야 할수 있습니다.
'로봇 > SLAM' 카테고리의 다른 글
| 그래프 기반 SLAM 튜토리얼 - 4.C 매니폴드에서 최소 제곱 (0) | 2020.07.08 |
|---|---|
| 그래프 기반 SLAM 튜토리얼 - 4.B 선형화된 시스템의 구조에 대한 고려사항들 (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 4. 그래프 기반 SLAM (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 3. 관련 연구들 (0) | 2020.07.08 |
| 그래프 기반 SLAM 튜토리얼 - 2. SLAM의 확률적 표현 (0) | 2020.07.08 |