3.2.2 칼만 필터 알고리즘
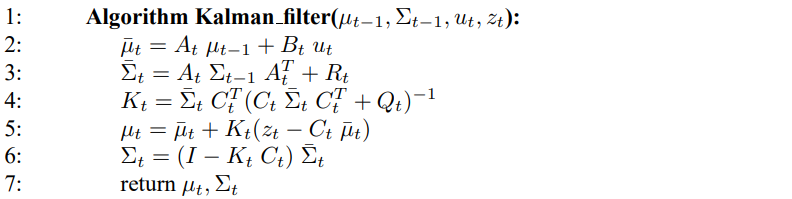
칼만 필터 알고리즘은 표 3.1과 같으며, 여기서 신뢰도 bel($x_t$)는 시간 t에 대해 평균 $\mu_t$, 공분산 $\Sigma_t$를 가집니다. 칼만 필터의 입력으로 시간 t-1일때의 신뢰도로 이 때 평균 $\mu_{t-1}$, $\Sigma_{t-1}$로 표현합니다. 이 값들을 갱신하기 위해 칼만 필터는 제어 입력 $u_t$와 측정 $z_t$가 필요하며, 그 결과가 시간 t에 대한 신뢰도가 됩니다.
2,3번째 줄에서 예측 신뢰도 $\bar{\mu}$, $\bar{\Sigma}$가 신뢰도 $\bar{bel} (x_t)$를 나타내고, $z_t$를 합치기 전의 값이 됩니다. 이 신뢰도는 제어 입력 $u_t$,를 합하여 구할수 있습니다. 이 평군치는 상태 전이 함수 (3.2)의 결정론적 형태를 이용하여 $x_{t-1}$ 대신 $\mu_{t-1}$로 대입하여 구할 수 있습니다. 공분산의 갱신을 하기 위해서는 선형 행렬 $A_t$를 통해 이전의 상태에서 구하며, 이 행렬은 공분산에 이차 형태로 곱해지게 되어, 공분산은 이차 행렬이 됩니다.
신뢰도 $\bar{bel}(x_t)$는 4 ~ 6줄의 과정을 통해 측정 $z_t$를 합쳐 신뢰도 $bel(x_t)$로 변형 됩니다. 여기서 4번 줄의 변수 $K_t$는 칼만 게인이라 부르며, 측정치를 새로운 상태 추정에 얼마나 반영할지 지정하는 이득으로 사용됩니다. 5번째줄에서 실제 측정치 $z_t$와 식 (3.5)의 측정 확률을 이용해 예측 측정치의 차이는 칼만 게인 $k_t$에 비례하여 평균값을 구하게 됩니다. 마지막으로 사후확률 신뢰도의 공분산은 6번재 줄과 같이 계산되는데 측정 치로부터 정보 게인을 조절을 하게 됩니다.
3.2.3 과정
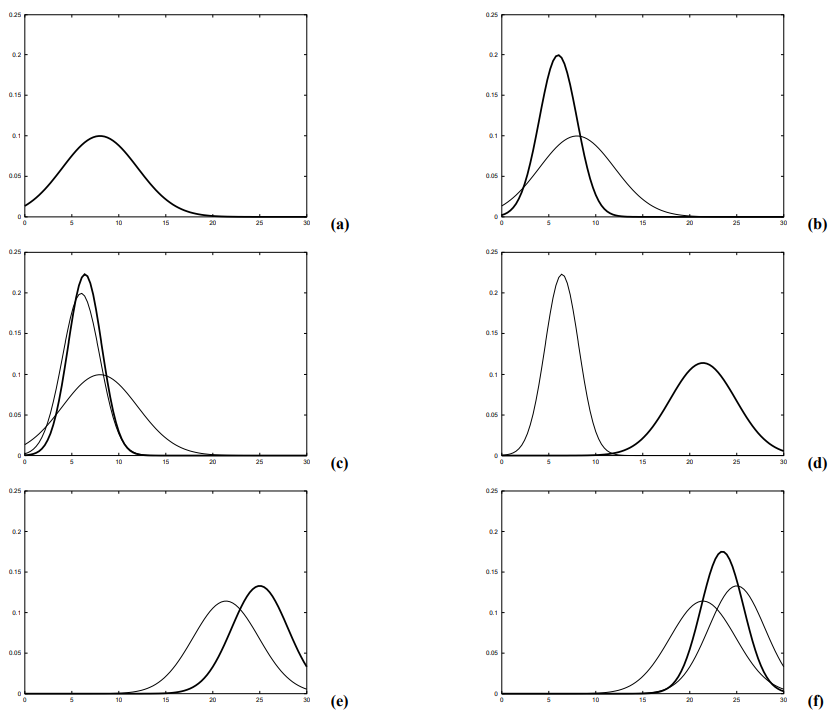
(a) 초기 신뢰도
(b) 측정치(굵은 가우시안)
(c) 칼만 필터 알고리즘을 이용해 측정치를 합쳐 구한 신뢰도
(d) 우측으로 이동후의 신뢰도(불확실성이 증가함)
(e) 새로운 측정
(f) 칼만 필터 수행후 구한 신뢰도
그림 3.2는 간단한 1차원 위치 추정 문제에서 칼만 필터 알고리즘의 수행과정을 보여줍니다. 그림 3.2의 각각의 다이어그램은 수평 축을 따라 로봇이 이동한다고 가정을 하고 있으며, 그림 3.2a에서 로봇의 위치 사전확률이 정규 분포로 주어지고 있습니다. 로봇은 gps와 같은 센서를 이용해 현재 위치를 확인하고 있으며, 그림 3.2b에서 굵은 가우시안의 꼭대기 중심이 측정치를 의미하고 있습니다. 이는 센서로 예측한 값으로 폭은 측정에서 불확실성에 대한 공분산을 의미합니다. 사전확률과 측정치를 합하여 표 3.1의 4~6줄 과정으로 그림 3.2c의 굵은 가우시안을 구하게 됩니다. 이는 기존의 두개의 평균 사이에 신뢰도의 평균이 존재하게 되며 그 값이 불확실성은 사용된 가우시안 분포 보다 작아지게 됩니다. 이는 칼만 필터의 정보 통합에 의한 기본적인 특성입니다.
다음으로 로봇이 우측으로 이동한다고 가정해봅시다. 그러면 불확실성은 증가하게 되고 칼만필터 알고리즘 2~3줄에 따라 그림 3.2d와 같은 가우시안 분포가 나ㅏ나게 됩니다. 이 가우시안은 로봇이 이동한 만큼 움직이게 되며 여러가지 이유로 폭이 커지게 됩니다. 그림 3.2f에서 굵은 가우시안으로 두번째 측정치를 구하고, 그림 3.2f에서 구한 사후확률을 굵은 가우시안으로 보여주고 있습니다.
이 예제는 칼만 필터에서 기존 신뢰도에 센서 데이터를 합치는 측정 갱신 과정(5 ~7 줄)과 동작 후 신뢰도의 변화를 보여주는 예측 과정을 보여주고 있습니다. 갱신 과정에서는 로봇 신뢰도 불확실성이 줄어드나 예측 과정에서는 불확실성이 커지는 모습을 볼 수 있습니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇공학 - 4 비모수적 필터 (0) | 2020.06.22 |
|---|---|
| 확률적 로봇공학 - 3.3 ~ 확장 칼만 필터 (0) | 2020.06.22 |
| 확률적 로봇공학 - 3 가우시안 필터 (0) | 2020.06.21 |
| 확률적 로봇공학 - 2.4.4 마르코브 가정 (0) | 2020.06.21 |
| 확률적 로봇공학 - 2.4 베이즈 필터 (0) | 2020.06.21 |