2.4 베이즈 필터 bayes filter
2.4.1 베이즈 필터 알고리즘
신뢰도 계산에서 사용되는 가장 일반적인 알고리즘으로 베이즈 필터가사용됩니다. 이 알고리즘은 신뢰도 분포 bel을 측정과 제어 데이터로 계산하게 되는데 우선 이 기본 알고리즘을 보고 수치적인 예시로 자세히 다뤄보겠습니다. 그러고 난 후 수학적으로 다루어 보겠습니다.

표 2.1은 기본 베이즈 필터의 슈도 알고리즘 형태로 베이즈 필터는 재귀적이므로 bel($x_t$)는 이전의 bel($x_{t-1}$)로부터 계산할 수 있습니다. 이 알고리즘의 입력은 시간 t-1에서의 신뢰도 bel과 최근의 제어 입력 $u_t$와 측정 $z_t$가 됩니다. 그리고 이 알고리즘의 출력은 시간 t에 대한 신뢰도 bel($x_t$)이 됩니다. 표 2.1은 베이즈 필터의 기본 단계인 갱신 법칙을 보여주고 있습니다. 이 갱신 법칙은 제귀적으로 수행되어 이전에 구한 bel($x_{t-1}$)로 bel($x_t$)를 구하는데 사용됩니다.
베이즈 필터 알고리즘은 2가지 필수적인 단계로 이루어지는데, 3번째 줄에서는 제어 $u_t$가 사용되어 사전확률로 상태 $x_{t-1}$과 제어 $u_t$를 이용하여 상태 $x_t$에 대한 신뢰도를 구하게 됩니다. 특히 신뢰도 $\bar{bel}$($x_t$)는 두 분포의 곱을 적분하여 상태 $x_t$를 구하는데, 이 때 $x_{t-1}$에 대한 사전확률과 제어 $u_t$가 $x_{t-1}$에서 $x_t$로 상태를 전이 시킬때의 확률를 사용합니다. 이는 식 (2.12)에서 본 갱신 과정과 비슷할 수 있는데 이 갱신 단계를 제어 갱신 control update나 예측 prediction이라 합니다.
베이즈 필터의 다음 단계로 측정 갱신 measurement update라 합니다. 베이즈 필터 알고리즘의 4번째 줄은 신뢰도 $\bar{bel}$($x_t$)를 측정 $z_t$에 대한 확률을 곱하게 됩니다. 이는 각 상태 사후확률 가정에 대해 적용이 됩니다. 곱의 결과는 일반적인 확률이 아니게되어 적분을 수행하지 않습니다. 그래서 이 결과는 정규화가 수행되어야 하는대 정규화 상수 $\eta$로 정규화를 수행합니다. 이 결과가 6번째 줄의 신뢰도 bel($x_t$)가 됩니다.
사후확률 신뢰도를 재귀적으로 계싼하기 위해서 이 알고리즘은 맨 처음의 신뢰도 bel($x_0$)이 필요한데, $x_0$에 대해 알고있다면 특정 지점 $x_0$을 중심으로 하는 분포로 초기화 하고 나머지에는 0으로 할당될겁니다. 하지만 초기값 $x_0$를 모른다면, bel($x_0$)은 균일 분포로 초기화가 되어야 합니다. 초기 값 $x_0$에 대해 일부분만 알고 있다면 비 균일 분포를 사용할 수 있지만 초기 값을 완전히 알거나 완전히 모르는 두 경우가 일반이게 됩니다.
2.4.2 예시
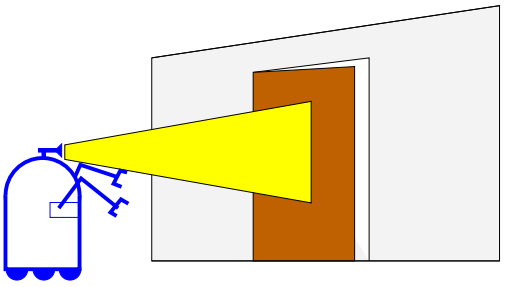
그림 2.2의 시나리오를 따라 베이즈 필터 알고리즘을 적용해보면, 여기서 로봇은 카메라를 이용해 문의 상태를 추정하고 있습니다. 이 문제를 쉽게 다루기 위해서 문에 대해서 2가지 상태(열림과 닫힘)만 존재한다고 가정하고, 로봇이 문의 상태를 바꿀수 있다고 합시다. 추가적으로 로봇은 처음에 문의 상태를 모른다고도 합시다. 대신, 두가지 문의 상태에 대해 다음과같이 똑같은 사전 확률을 주어봅시다.

로봇의 센서는 노이즈를 가지고 있으므로 노이즈는 다음과 같은 조건부 확률로 나타내어 보겠습니다.


이 확률들을 보면 로봇의 센서는 닫힌 문을 감지하는 경우 에러 확률이 0.2가 될만큼 더 신뢰할수 있음을 볼 수 있습니다. 하지만 문이 열린 경우 잘못 측정할 가능성이 0.4만큼이나 됩니다.
마지막으로 로봇이 매니퓰레이터로 문을 밀어 연다고 생각해봅시다. 문이 이미 열려있다면, 열린 채 일것이고 닫힌 경우에는 0.8의 확률로 열리게 될것입니다.
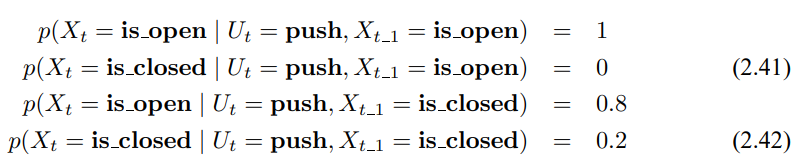
물론 매니퓰레이터를 사용하지 않는 경우도 존재하며 이 때 상태는 바뀌지 않을겁니다. 이를 조건부 확률로 다음과 같이 정리 할수있습니다.
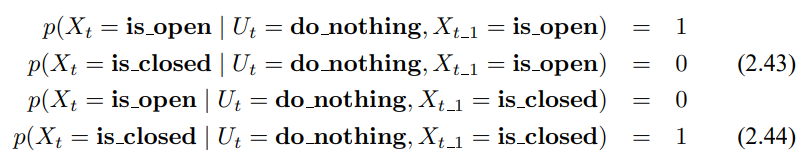
시간 t에 대해서 로봇이 아무런 제어 동작을 하지 않았지만 문이 열려있다고 인식했다고 합시다. 결과 사후확률 신뢰도는 사전 확률 신뢰도 bel($X_0$)과 제어 $u_1$ = do_nothing, 측정 sense_open을 입력으로 하는 베이즈 필터로 구할 수 있습니다. 상태 공간은 유한하므로 3번째 줄의 적분을 유한 개의 합으로 나타내면 다음과 같습니다.
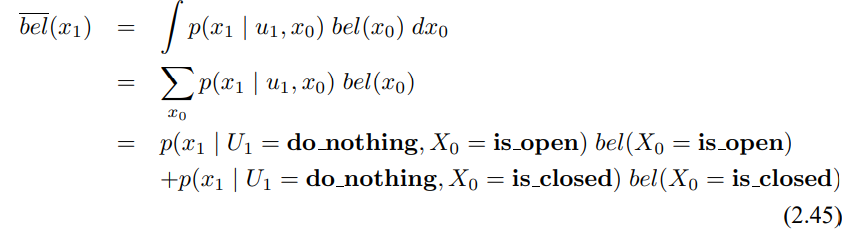
여기서 상태 변수 $X_1$에 대한 두가지 값을 정리할수 있는데, $X_1$ = is_open이라면 다음과 같이 정리 할 수 있습니다.
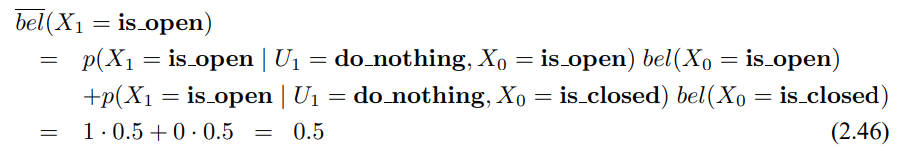
이처럼 $X_1$인 경우에도 아래와 같이 구할 수 있습니다.
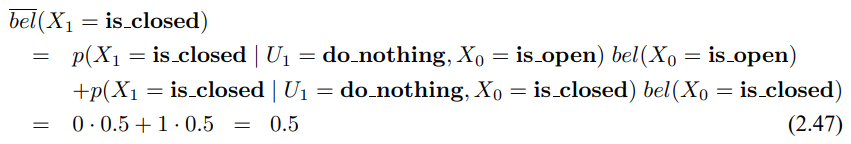
우리가 구한 신뢰도 $\bar{bel}$($x_1$)은 사전 신뢰도 $x_0$와 같은데, 동작이 do_nothing이므로 상태에 영향을 주지 않으니 같더라도 놀랄 일은 아닙니다.
하지만 측정을 합치면 신뢰도가 변하게 됩니다. 베이즈 필터 알고리즘의 4번째 줄을 따라
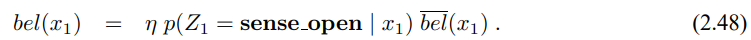
우리가 구한 두가지 경우인 $X_1$ = is_open과 $X_1$ = is_closed 구하면 다음의 결과를 얻을 수 있습니다.

정규자 $\eta$는 다음과 같이 계산할수 있으니

베이즈 필터를 이용해 구한 결과는 다음과 같습니다

다음 시간에 대해서 쉽게 개산할 수 있는데 이번에는 $u_2$ = push 이고, $z_2$ = sense_open 이라면 아래와 같이 계산할 수 있습니다.

'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇공학 - 3 가우시안 필터 (0) | 2020.06.21 |
|---|---|
| 확률적 로봇공학 - 2.4.4 마르코브 가정 (0) | 2020.06.21 |
| 확률적 로봇공학 - 2.3.3~ 확률 생성 법칙과 신뢰도 분포 (0) | 2020.06.20 |
| 확률적 로봇공학 - 2.3 로봇 환경 인터렉션 (0) | 2020.06.20 |
| 확률적 로봇공학 - 2.1 재귀적인 상태 추정 (0) | 2020.06.20 |