2.3.3 확률생성법칙 probabilistic generative laws
상태와 측정값은 확률 법칙이 적용됩니다. 그래서 보통 시간에 대한 상태 $x_t$는 확률적으로 만들어지게되고 확률 분포로 나타내게 됩니다. 우선 상태 $x_t$는 과거의 모든 상태와 측정, 제어에 조건부이므로 다음 혀앹의 확률 분포로 상태를 나타낼 수 있습니다.

그러나 상태 x가 완전하다면 이전 시간이 발생한 모든 것들의 결과라고 볼수 있습니다. $x_{t-1}$은 이전 모든 제어 $u_{1:t-1}$와 측정 $z_{1:t-1}$의 결과가 됩니다. 위를 이용해서 상태 $x_{t-1}$를 알고 제어 $u_t$만 중요하다고 하면 확률적인 용어로 이를 다음의 식으로 나타낼 수 있습니다.
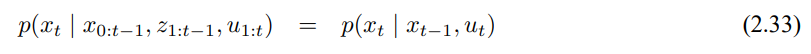
이러한 식은 조건부 독립의 예시를 보여주는데, 조건부 독립은 전반적으로 계속 다룰것이며 확률론적 로봇공학 알고리즘을 추적하는데 주요하게 사용됩니다.
비슷하게 측정이 수행되는 과정을 모델할때 $x_t$가 완전한 경우, 조건부 독립으로 다음과 같이 중요한 식을 구할 수 있습니다.
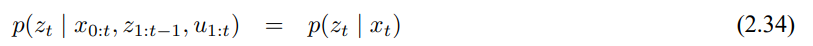
이는 상태 $x_t$로 측정 $z_t$를 예측하는데 충분한 것으로, 상태 $x_t$가 완전하다면 이전의 측정이나 제어, 상태 값들에 대해 알 필요가 없습니다.
두 조건부 확률 p($x_t$ | $x_{t-1}$, $u_t$)와 p($z_t$ | $x_t$)를 다루어 봅시다. 우선 확률 p($x_t$ | $x_{t-1}$, $u_t$)는 상태 전이 확률로 state transition probability 로봇 제어 $u_t$의 함수로 어떻게 상태를 진행시킬지를 알려줍니다. 로봇 환경은 확률론적이므로 p($x_t$ | $x_{t-1}$, $u_t$)는 결정론적인 함수가 아니라 확률분포가 됩니다. 때떄로 상태 전이 확률 분포는 시간 t에 의존하지 않을수 있습니다.
확률 p($z_t$ | $x_t$)는 측정 확률 measurement probability로 시간 t에 대해 의존하지 않을때는 p(z|x)로 쓸 수 있습니다. 측정 확률은 주위 환경 상태 x로부터 측정된 z에 대해 알려주며, 측정은 노이즈가 존재하는 상태의 사영이 됩니다.
상태 전이 확률과 측정 확률은 함께 사용하여 로봇과 주위 환경의 동적 확률시스템을 나타냅니다.
2.3.4 신뢰도 분포 Belief Distribution
확률론적 로봇공학에서 다른 주요 컨샙으로 신뢰도 belief가 있습니다. 이 신뢰도는 환경 상태 중에서 로봇에 관한 정보들을 알려주는데 이미 상태는 직접적으로 측정할수 없다고 했었습ㄴ디ㅏ. 예를 들어 로봇의 위치가 x = <14.12, 12.7, 0755>에 존재하더라도, 로봇은 GPS없이는 스스로의 위치를 직접 측정할수 없으므로 알 수가 없습니다. 대신 로봇은 데이터로부터 자세를 추론해야내만 하는데, 진짜 상태와 상태에 대한 지식을 신뢰도로 구분해서 다루겠습니다.
확률론적 로봇공학은 신뢰도를 조건부 확률 분포로 나타냅니다. 신뢰도 분포는 가정이 주어질때 진짜 상태에 대한 확률로 주어진 데이터에 대한 상태 변수들의 조건부 사후 확률입니다. 상태 변수 $x_t$에 대한 신뢰도를 bel($x_t$라 하며, 사후확률로 아래와 같이 표기 할 수 있습니다.

이 사후확률은 모든 이전의 측정 $z_{1:t}$과 제어 $u_{1:t}$가 주어질때 시간 t에 대한 상태 $x_t$의 확률 분포가 됩니다.
이 내용을 보다보면 신뢰도는 측정 $z_t$를 합한 구에야 구할수 있다고 볼수 있지만, 제어 $u_t$를 수행한 후 $z_t$를 합치기 전에 사후확률을 계산하여 유용하게 사용할 수 있습니다. 이 사후확률은 다음과 같이 표기합니다.

이 확률 분포는 확률 필터링 과정에서 예측 과정이라고도 부르며 이 용어는 $\bar{bel}$($x_t$)는 이전의 상태 사후확률를 이용하여 시간 t에서 측정을 합치기 전의 상태를 예측하는 것을 의미하게 됩니다. $\bar{bel}$($x_t$)로부터 bel($x_t$)를 계산하는 과정을 측정 갱신/갱신 mearuement update/correction이라 합니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇공학 - 2.4.4 마르코브 가정 (0) | 2020.06.21 |
|---|---|
| 확률적 로봇공학 - 2.4 베이즈 필터 (0) | 2020.06.21 |
| 확률적 로봇공학 - 2.3 로봇 환경 인터렉션 (0) | 2020.06.20 |
| 확률적 로봇공학 - 2.1 재귀적인 상태 추정 (0) | 2020.06.20 |
| 확률적 로봇공학 - 1 소개 (2) | 2020.06.20 |