확률 생성 법칙 probabilistic generative laws
제 1법칙
신뢰도는 상태 $x_t$로 나타내며, 이 값은 모든 이전 상태와 측정, 그리고 제어 입력이 주어질 때 구할수 있는데, 이 조건부 확률은 수학적으로 정리하면 다음과 같습니다.

1. $z_t$는 측정
2. $u_t$ 동작 명령
3. $x_t$는 시간 t에 대한 로봇이나 주위 환경의 상태(위치, 속도 등)
만약 우리가 상태 $x_{t-1}$과 $u_t$를 알고 있다면, 상태 $x_{0:t-2}$와 $z_{1:t-1}$는 조건부 독립 성질에 따라 아는게 크게 중요하지는 않습니다. 상태 $x_{t-1}$는 $x_t$와 $z_{1:t-1}$, $u_{1:t1}$ 사이 조건부 독립을 나타내는데 사용됩니다. 이를 정리하면 다음과 같습니다.

2법칙
$x_t$가 완전하다면

여기서 $x_t$가 완전하다는것의 의미는 과거의 상태, 측정, 동작 명령이 미래를 예측하는데 필요한 정보를 주지않는 경우를 말합니다.
$x_{0:t-1}$, $z_{1:t-1}$, $u_{1:t}$는 조건부 독립인 $x_t$가 주어질때 $z_t$와 같습니다.
이 필터는 아래의 두 가지의 파트로 이루어 집니다.
p($x_t$ | $x_{t-1}$, $u_t$) -> 상태 전이 확률 state trasition probability
p($z_t$ | $x_t$) -> 측정 확률
조건부 의존과 조건부 독립의 예제
- 독립인 경우와 조건부 의존하는 경우
2개의 양면 동전이 있다고 합시다.
A - 첫번째 동전이 앞면을
B - 두 번째 동전이 앞면을
C - 두 동전이 같은 경우
A와 B만 보면 독립이지만, C가 주어진 경우라면 A와 B는 조건부 독립이 됩니다. C라는 사실을 알고 있다면 첫번째 동전의 결과가 다른 것의 결과도 알려주기 때문입니다.
- 의존하는 경우와 조건부 독립인 경우
어느 상자에 2개의 동전이 있는데 1개는 일반적인 동전이고 하나는 둘다 동일한 가짜 동전이라고 합시다(P(H) = 1). 동전을 하나 고르고 던지는 것을 2번 해보면 이 사건들을 다음과 같이 정의할 수 있습니다.
A = 첫 코인이 앞면이 나온 경우
B = 두 번째 동전이 앞면이 나오는 경우
C = 일반 동전을 골른 경우
A가 발생한 경우, 우리가 일반 코인 보다는 가짜 코인을 고른 가능성이 더 크다고 볼 수 있습니다. 이는 B가 발생할 조건부 확률을 증가시키는데, A와 B는 의존 관계임을 의미합니다. 하지만 C라는 사실이 주어질 때는 A와 B는 서로 독립이 됩니다.
베이즈 법칙 bayes rule
사후 확률 posterior P(B | A) = $\frac{우도 Likelihood P(A|B) * 사전 확률 prior P(B)} {주변 확률 분포 Marginal P(A)}$
여기서
- 사후 확률 : A라는 사건 일어났을때, 사건 B가 일어날 확률
- 우도 : 사건 B가 일어났을때, A인 확률
- 사전 확률 : 사건 B가 일어날 확률
- 주변 확률 : 사건 A가 일어날 확률
예제 :
여성 중 1%는 유방암을 가지고 99%는 그렇지 않습니다. 유방함 검사로 80%의 경우 유방암을 찾아내지만 20%는 놓치게 됩니다. 유방암 검사에서 9.6%는 유방암이 존재하지 않지만 유방암이 있다고 잘못 찾아냅니다.
베이즈 정리로 이를 식으로 정리하면 다음과 같이 정리할 수 있습니다.
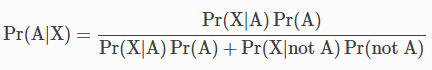
- Pr(A|X) - 양성 (X)인데, 실제로 암을 가진 (A) 확률을 위 식을 이용해서 구하면 7.8%가 됩니다.
- Pr(X|A) - 암을 가진 경우 (A), 양성인 (X) 경우 이는 참 긍정으로 80%가 됩니다.
- Pr(A) - 암이 있는 경우 1%
- Pr(not A) - 암이 없는 경우 99%
- Pr(X | not A) - 암이 없는데 (~A) 양성 (X)이 된 경우, 이는 거짓 긍정 false positive으로 9.6%가 됩니다.
베이즈 필터 알고리즘
기본 필터 알고리즘은 $x_t$에 대해 다음과 같이 정리 할 수 있습니다.
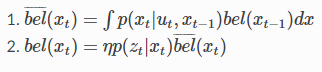
예측 단계
첫 번째 단계는 베이즈 정리 bayes theorem을 이용하여 사전확률을 구하는데 이를 예측 과정 prediction step이라 합니다. 신뢰도 $\bar{bel}(x_t)$는 시간 t일때 측정 $z_t$를 반영하기 이전으로 이 단계에서는 동작이 발생함에 따라 기존의 가우시안과 공분산이 더해져 기존 정보를 잃어버리게 됩니다. 이 방정식의 RHS(right hand side) 우항은 사전 확률 계산을 위해서 전체 확률 법칙 law of total probabily를 사용합니다.
갱신 단계
다음은 갱신 단계로 correction or update step 시간 t에서의 측정 $z_t$를 통합하여 로봇의 신뢰도를 계산하는데, 로봇이 어디에 있는지 센서 정보로 반영하며 구하며 여기서 가우시안 분포들을 곱하게 됩니다. 가우시안의 곱 연산 결과로 평균은 사이에 위치하고, 공분산은 작아지게 됩니다.

위 그림은 베이즈 필터로 로봇의 위치를 추정하는 예시로서 로봇은 복도가 어떻게 생겼는지는(지도) 알지만 자신의 위치를 모르는 상태 입니다.
1. 맨 처음, 로봇은 지도상에서 어디에 위치하는지 모르므로 지도 전체에 동일한 확률들을 배정합니다.
2. 첫 센서 결과로 문이 존재하는것을 알았습니다. 로봇은 지도가 어떻게 되어있는지 알고는 있으나 문이 3개가 있으므로 어디에 있는지는 아직 알 수 없습니다. 그래서 각각의 문 위치에다가 같은 확률들이 배정됩니다.
3. 로봇이 앞으로 전진하면서 예측과정이 발생하는데 일부 정보를 잃어버리므로 4번째 다이어그램 처럼 가우시안의 분산이 커지게 됩니다. 마지막으로 신뢰도 분포는 이전 단계서의 사후확률과 동작후 상태를 컨볼루션한 결과로 평균이 우측으로 이동하게 됩니다.
4. 다시 측정 결과를 반영을 하는데 문이 존재한다면, 세 문들 앞에서 모두 문이 존재할 확률들은 같으므 5번째 다이어그램에서 계산한 사후확률을 구할 수 있습니다. 이 사후확률은 이전 사후확률과 측정의 컨벌루션 결과이며 로봇이 2번째 문 근처에 있음을 알 수 있습니다. 이때 분산은 작아지며 확률은 커지게 됩니다.
5. 이러한 동작과 갱신 과정이 반복되면 로봇은 6번째 다이어그램처럼 주위 환경에 대해 자신의 위치를 추정할 수 있게 됩니다.
베이즈 필터와 칼만 필터 구조
칼만 필터의 기본 구조와 컨셉은 베이즈 필터와 동일합니다. 다만 차이점은 칼만 필터의 수학적인 표현법인데, 칼만 필터는 가우시안을 이용한 베이지안 필터가 아닙니다. 베이즈 필터를 칼만 필터에 적용하기 위해서 가우시안을 히스토그램이 아닌 방법으로 나타낼건데, 베이즈 필터의 기본 공식은 다음과 같습니다.

$\bar{x}$는 사전 확률
$\iota$는 사전 확률 $\bar{x}$가 주어질때 측정에 대한 우도
$f_x$($\cdot$)은 속도를 이용해서 다음 위치를 예측할때 사용하는 모델이 됩니다.
*는 컨볼루션을 의미합니다.
칼만 게인

위에서 x는 사후확률이며 $\iota$와 $\bar{x}$는 가우시안이 됩니다.
그러므로 이 사후확률의 평균은 다음과 같이 정리할 수 있습니다.
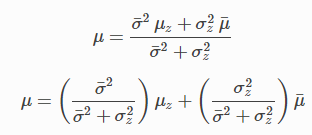
다음과 같은 형태로 사전확률과 측정치를 스캐일링을 할수 있는데

여기서 분모가 정규화 시키므로 가중치를 하나에 합치며 K = $W_1$로 정리하면 다음과 같습니다.

칼만 게인에서의 분산은 다음과 같습니다.
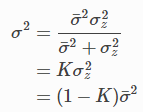
K는 칼만게인이라 하며 측정치 $\mu_z$와 예측 평균 $\bar{\mu}$ 사이 값을 얼마나 반영할지 스케일링하는데 사용됩니다.
칼만 필터 - 단변수와 다변수
예측 단계

갱신 단계

레퍼런스
1. 로저 라베의 칼만 필터 관련 저장소
github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python
2. 세바스찬 스런의 probabilistic robotics
'로봇 > 로봇' 카테고리의 다른 글
| 칼만, 베이즈 필터 - 파티클 필터 개요와 몬테카를로 방법 (0) | 2020.06.20 |
|---|---|
| 파이썬 로보틱스 - 위치추정, 확장 칼만 필터 (0) | 2020.06.20 |
| 칼만과 베이즈 필터 in python (0) | 2020.06.19 |
| 파이썬 로보틱스 - 칼만 필터 기초 파트 1 (0) | 2020.06.18 |
| 파이썬 로보틱스 (1) | 2020.06.18 |