왜 확률 밀도 함수 PDF로 신뢰도 belief를 나타내는데 사용하는가?
로봇이 동작하는 환경은 확률론적이기 때문입니다. 로봇과 주위 환경은 (시간에 대한 함수인)결정론적인 모델이 될수 없는데, 현실 세계의 센서들은 에러를 포함하고 있어 그 센서에 대한 평균과 분산으로 나타냅니다. 그래서 앞으로 평균과 분산을 이용한 모델을 다루게 될 것 입니다.
확률 변수의 기대값이란 무엇인가? expectation of a random variable
기대값은 확률의 평균 뿐만이 아니라

연속 영역에서의 형태로도 나타낼 수 있습니다.

import numpy as np
import random
x=[3,1,2]
p=[0.1,0.3,0.4]
E_x=np.sum(np.multiply(x,p))
print(E_x)

멀티모달보다 유니모달로 신뢰도를 나타내는 경우 이점은 무엇인가?
What is the advantage of representing the belief as a unimodal as opposed to multimodal?
움직이는 자동차의 위치를 두 가지 확률로 나타내는건 햇갈리므로 효율적이지는 않습니다.
분산, 공분산, 상관계수
분산
분산은 데이터가 퍼진 정도를 의미하며, 평균은 데이터가 얼마나 많은지를 나타내지는 않습니다.
x=np.random.randn(10)
np.var(x)
공분산
다변수 분포 multivariate distribution인 경우에 사용되는데, 예를 들면 2차원 공간에서의 로봇은 위치를 나타내는데 x, y 값을 사용할겁니다. 이를 나타내기 위해서 평균이 x, y인 정규 분포가 사용됩니다.
다변수 분포에서 평균 $\mu$는 아래의 행렬로 나타낼수 있는데
이처럼 분산도 표현할 수 있습니다.
하지만 중요한 점은 모든 변수들은 그 값에 대해 분산을 가지고 있는 점인데, 각각의 확률 변수들이 어떻게 서로 다른 형태 존재하도록 가능해 집니다. 역시 이 두 데이터셋에는 그들이 얼마나 관련되어있는지를 의미하는 상관 계수와도 관련 있습니다.
예를 들자면 보통 키가 증가하면 몸무게도 증가하는데, 이러한 변수들은 서로 상관관계를 가진다고 할 수 있습니다. 이 값들은 한 변수가 커지면 다른것도 커지므로 양의 상관 관계가 가진것이 됩니다.
이제 다변수 정규분포의 공분산을 공분산 행렬 covariance matrix를 사용해서 다음과 같이 나타내겠습니다.

대각 성분 diagonal : 각 변수들의 분산
비대각 성분 off-diagonal : $i_{th}$ 변수와 $j_{th}$ 변수의 공분산

x=np.random.random((3,3))
np.cov(x)
가우시안 Gaussian
중심 극한 이론 Central Limit Thorem
이 이론에 따르면, 독립 확률 변수 n개 샘플의 평균은 샘플 사이즈를 늘릴수록 정규 분포의 형태가 되는 경향이 있습니다.(일반적으로 n >= 30)
import matplotlib.pyplot as plt
import random
a=np.zeros((100,))
for i in range(100):
x=[random.uniform(1,10) for _ in range(1000)]
a[i]=np.sum(x,axis=0)/1000
plt.hist(a)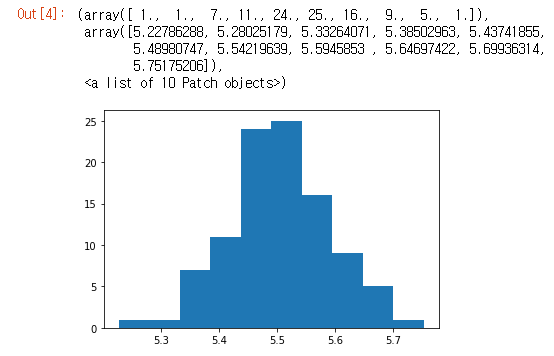
가우시안 분포 gaussian distribution
가우시안은 연속 확률 분포 중 하나로 평균 $\mu$와 분산 $\sigma^2$ 두개의 파라미터로 나타내며 정의는 아래와 같습니다.

이는 평균 $\mu$과 표준편차 $\sigma$의 함수로서 종 모양이 되는 정규 분포의 특성을 나타냅니다.
import matplotlib.mlab as mlab
import math
import scipy.stats
mu = 0
variance = 5
sigma = math.sqrt(variance)
x = np.linspace(mu - 5*sigma, mu + 5*sigma, 100)
plt.plot(x,scipy.stats.norm.pdf(x, mu, sigma))
plt.show()
가우시안의 성질 Gaussian Properties
곱 multiplication
베이즈 필터 bayes filter의 측정 갱신 measurement update에서 그 알고리즘은 사전 확률 P($X_t$)와 측정 확률 P($Z_t$ | $X_t$)를 다음의 사후 확률을 구하기 위해 곱하여야 합니다.
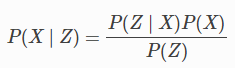
여기서 분자 P(Z | X), P(X)는 N($\bar{\mu}$, $\bar{\sigma}^{1}$), N($\bar{\mu}$, $\bar{\sigma}^{2}$)을 따르는 가우시안이 됩니다.
곱 연산으로 구한 새로운 평균은
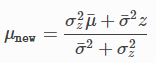
새로운 분산은

import matplotlib.mlab as mlab
import math
mu1 = 0
variance1 = 2
sigma = math.sqrt(variance1)
x1 = np.linspace(mu1 - 3*sigma, mu1 + 3*sigma, 100)
plt.plot(x1,scipy.stats.norm.pdf(x1, mu1, sigma),label='prior')
mu2 = 10
variance2 = 2
sigma = math.sqrt(variance2)
x2 = np.linspace(mu2 - 3*sigma, mu2 + 3*sigma, 100)
plt.plot(x2,scipy.stats.norm.pdf(x2, mu2, sigma),"g-",label='measurement')
mu_new=(mu1*variance2+mu2*variance1)/(variance1+variance2)
print("New mean is at: ",mu_new)
var_new=(variance1*variance2)/(variance1+variance2)
print("New variance is: ",var_new)
sigma = math.sqrt(var_new)
x3 = np.linspace(mu_new - 3*sigma, mu_new + 3*sigma, 100)
plt.plot(x3,scipy.stats.norm.pdf(x3, mu_new, var_new),label="posterior")
plt.legend(loc='upper left')
plt.xlim(-10,20)
plt.show()
덧셈 Addition
동작 단계 motion step에서는 확률을 더하게 되는데, 여기서 사용되는 두 가우시안인 신뢰도들이 합하여야 합니다. 아래는 두 확률의 덧셈 예시가 됩니다.

import matplotlib.mlab as mlab
import math
mu1 = 5
variance1 = 1
sigma = math.sqrt(variance1)
x1 = np.linspace(mu1 - 3*sigma, mu1 + 3*sigma, 100)
plt.plot(x1,scipy.stats.norm.pdf(x1, mu1, sigma),label='prior')
mu2 = 10
variance2 = 1
sigma = math.sqrt(variance2)
x2 = np.linspace(mu2 - 3*sigma, mu2 + 3*sigma, 100)
plt.plot(x2,scipy.stats.norm.pdf(x2, mu2, sigma),"g-",label='measurement')
mu_new=mu1+mu2
print("New mean is at: ",mu_new)
var_new=(variance1+variance2)
print("New variance is: ",var_new)
sigma = math.sqrt(var_new)
x3 = np.linspace(mu_new - 3*sigma, mu_new + 3*sigma, 100)
plt.plot(x3,scipy.stats.norm.pdf(x3, mu_new, var_new),label="posterior")
plt.legend(loc='upper left')
plt.xlim(-10,20)
plt.show()
이번 예시는 이변수 가우시안 분포 bivariate gaussian distribution를 시각화하는 예제로 2차원 표면에서 나오는 결과를 3차원으로 사영한 결과를 보여줍니다. 타원에서 가장 깊은 곳은 가장 높은 부분으로 주어진 (x,y)의 최대 확률이 됩니다.
#Example from:
#https://scipython.com/blog/visualizing-the-bivariate-gaussian-distribution/
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
# Our 2-dimensional distribution will be over variables X and Y
N = 60
X = np.linspace(-3, 3, N)
Y = np.linspace(-3, 4, N)
X, Y = np.meshgrid(X, Y)
# Mean vector and covariance matrix
mu = np.array([0., 1.])
Sigma = np.array([[ 1. , -0.5], [-0.5, 1.5]])
# Pack X and Y into a single 3-dimensional array
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y
def multivariate_gaussian(pos, mu, Sigma):
"""Return the multivariate Gaussian distribution on array pos.
pos is an array constructed by packing the meshed arrays of variables
x_1, x_2, x_3, ..., x_k into its _last_ dimension.
"""
n = mu.shape[0]
Sigma_det = np.linalg.det(Sigma)
Sigma_inv = np.linalg.inv(Sigma)
N = np.sqrt((2*np.pi)**n * Sigma_det)
# This einsum call calculates (x-mu)T.Sigma-1.(x-mu) in a vectorized
# way across all the input variables.
fac = np.einsum('...k,kl,...l->...', pos-mu, Sigma_inv, pos-mu)
return np.exp(-fac / 2) / N
# The distribution on the variables X, Y packed into pos.
Z = multivariate_gaussian(pos, mu, Sigma)
# Create a surface plot and projected filled contour plot under it.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z, rstride=3, cstride=3, linewidth=1, antialiased=True,
cmap=cm.viridis)
cset = ax.contourf(X, Y, Z, zdir='z', offset=-0.15, cmap=cm.viridis)
# Adjust the limits, ticks and view angle
ax.set_zlim(-0.15,0.2)
ax.set_zticks(np.linspace(0,0.2,5))
ax.view_init(27, -21)
plt.show()
'로봇 > 로봇' 카테고리의 다른 글
| 칼만, 베이즈 필터 - 파티클 필터 개요와 몬테카를로 방법 (0) | 2020.06.20 |
|---|---|
| 파이썬 로보틱스 - 위치추정, 확장 칼만 필터 (0) | 2020.06.20 |
| 칼만과 베이즈 필터 in python (0) | 2020.06.19 |
| 파이썬 로보틱스 - 칼만 필터 기초 파트 2 (0) | 2020.06.19 |
| 파이썬 로보틱스 (1) | 2020.06.18 |