728x90
캐글의 자전거 대여 수요 예측 문제
www.kaggle.com/c/bike-sharing-demand/data
일단 라이브러리 임포트
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
관련 데이터셋 로드

samples = pd.read_csv("./res/bike-sharing-demand/sampleSubmission.csv")
train = pd.read_csv("./res/bike-sharing-demand/train.csv")
test = pd.read_csv("./res/bike-sharing-demand/test.csv")
train.head()
데이터 확인하기

"""
session : 계절
holiday : 공휴일 여부
workingday : 평일 여부
weather : 날씨
temp : 온도
atemp : 체감온도
humidity : 습도
windspeed : 풍속
casual : 대여 회수
registered : 등록자의 대여횟수
count : 대여횟수
10886 x 12
na는 없음
"""
train.info()
날짜의 경우 문자열로 되어있으므로 datetime으로 변환
+ 년월일시간으로 분리

"""
문자열 날짜 -> datetime으로 변환
"""
train["datetime"] = train.datetime.apply(pd.to_datetime)
train["year"] = train.datetime.apply(lambda x : x.year)
train["month"] = train.datetime.apply(lambda x : x.month)
train["day"] = train.datetime.apply(lambda x : x.day)
train["hour"] = train.datetime.apply(lambda x : x.hour)
train.head()
필요없는 열 제거
datetime + casual, registered(count에 포함되므로)
"""
casual + registered = count
-> casual, registered, datetime 열 삭제
"""
drop_col = ["casual", "registered", "datetime"]
train.drop(columns=drop_col, axis=1, inplace= True)
성능 평가 지표들 정의
* np.log1p(val) : val + 1 후 로그 변환 수행
=> val = 0인 경우 -inf 방지
from sklearn.metrics import mean_squared_error, mean_absolute_error
#get root mean sqaured log error
def get_rmsle(y, pred):
log_y = np.log1p(y)
log_pred = np.log1p(pred)
mlse = np.sum((log_y - log_pred)**2)
rmlse = np.sqrt(mlse)
return rmlse
def get_rmse(y, pred):
return np.sqrt(mean_squared_error(y, pred))
def eval_reg(y, pred):
rmlse = get_rmsle(y, pred)
rmse = get_rmse(y, pred)
mae = mean_absolute_error(y, pred)
print("rmlse : {0:.3f}\nrmse : {1:.3f}\nmae : {2:.3f}".format(rmlse, rmse, mae))
단순 선형 회귀 학습 후 평가
- 성능 평가 지표들 오차 값이 크게 나옴

from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LinearRegression, Ridge, Lasso
y = train["count"]
X = train.drop(columns=["count"], axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
lr = LinearRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
eval_reg(y_test, pred)
오차가 가장 큰 값들 비교
실제 값과 예측 값사이 상당히 큰 오차
-> 타겟 값의 분포가 왜곡될 가능성이 큼

"""
종속 변수 count 값을 생각하면 오차가 상당히 크게 나옴
오차가 가장 큰 경우를 비교해보자
"""
def get_top_error_data(y_test, pred, n_tops = 5):
res = pd.DataFrame(data=y_test.values, columns=["real"])
res["predicted"] = pred
res["diff"] = np.abs(res["real"] - res["predicted"])
print(res.sort_values("diff", ascending=False)[:n_tops])
get_top_error_data(y_test, pred, n_tops=5)
라벨 분포 히스토그램으로 시각화
로그 변환을 통해 정규분포에 가깝게 변환

"""
예측 오류가 매우 큰것을 보면 타깃이 왜곡된 분포를 따르는지 확인해야함
"""
y.hist()
이전에 0을 중심으로 하던 분포가
5~6을 중심으로 정규 분포와 유사해짐

"""
로그 변환을 통해 y를 정규분포 형태로 바꾸어 주자
"""
y = np.log1p(y)
y.hist()
변환된 데이터로 재학습 및 성능 평가
rmse, mae는 크게 줄어들었으나 rmlse는 여전히 큼
-> 계수 확인해보자

"""
로그 변환을 수행 후
오차 척도들이 크게 줄어들었다.
"""
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
lr = LinearRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
eval_reg(y_test, pred)
get_top_error_data(y_test, pred, n_tops=5)
트리 모델에서 feature_importances_로 보았으나
회귀 모델에서 coef_로 볼수있음
"""
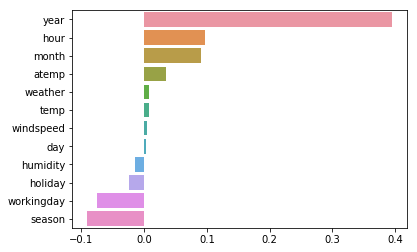
회귀 모델에서 피처 중요도로 보았던것과는 달리
선형 회귀 모델에선 회귀 계수로 어떤 피처가 중요하게 판단되었는지 몰수 있음
"""
coeff = pd.Series(data=lr.coef_, index=X.columns)
coeff_sort = coeff.sort_values(ascending=False)
sns.barplot(x=coeff_sort.values, y=coeff_sort.index)
카테고리형 데이터들을
원핫 인코딩으로 변환 후
학습, 결과 출력
rmlse도 어느정도 줄어듦

"""
상대적으로 큰 값을 갖는 year가 높은 중요도를 가진것으로 나오고 있음
year 간에는 큰 의미가 없는데도 영향을 주고 있으니
카테고리형 변수들을 인코딩 필요
"""
X_ohe = pd.get_dummies(X, columns=["year", "month", "hour", "holiday", "workingday",
"season", "weather"])
X_train, X_test, y_train, y_test = train_test_split(X_ohe, y, test_size = 0.3)
lr = LinearRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
eval_reg(y_test, pred)
get_top_error_data(y_test, pred, n_tops=5)
300x250
'인공지능' 카테고리의 다른 글
| 파이썬머신러닝 - 28. 차원 축소와 주성분 분석 (0) | 2020.12.10 |
|---|---|
| 파이썬머신러닝 - 27. 고급 회귀 기법을 이용한 주택 가격 예측 (0) | 2020.12.10 |
| 파이썬머신러닝 - 25. 트리기반 회귀분석 (0) | 2020.12.08 |
| 파이썬머신러닝 - 24. 로지스틱 회귀 분석 (0) | 2020.12.07 |
| 파이썬머신러닝 - 23. 선형 회귀 모델 데이터 변환 (0) | 2020.12.07 |