728x90
선형 회귀 모델은 기본적으로 오차항은 정규 분포를 따르고 있어
데이터의 분포가 정규분포를 따르는 것이 좋다.
하지만 분포가 한 방향으로 치우쳐진(왜도 != 0) 경우 예측 성능이 저하 될 수 있다.
-> 정규화 수행
1. 표준 정규 분포를 따르도록 정규화
- StandardScaler 사용
2. 최소 0, 최대 1이 되도록 정규화
- MinMaxScaler 사용
3. 로그 변환을 이용한 정규화
- 입력 데이터에 로그 변환 적용 -> 출력 값은 정규 분포를 따르게 됨.
데이터 변환 방법에 따른 성능을 비교하기 위해
이전의 선형 회귀 평가 함수에서 알파 값별 rmse를 반환하도록 약간 수정
def get_linear_reg_eval(model_name, params=None, X_data = None, y_target=None, visualize=False, columns=None):
fig, axs = plt.subplots(figsize=(18, 6), nrows=1, ncols=5)
coeff_df = pd.DataFrame()
print("#### {} ####".format(model_name))
params = params.copy()
rmses = []
for pos, param in enumerate(params):
if model_name == "Ridge": model = Ridge(alpha=param)
elif model_name == "Lasso": model= Lasso(alpha=param)
elif model_name == "ElasticNet": model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data, y, scoring="neg_mean_squared_error",cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
rmses.append(avg_rmse)
print("# alpha = {} #".format(param))
print("neg_mse_socres : {}".format(neg_mse_scores))
print("rmse_scores : {}".format(rmse_scores))
print("avg_rmse : {}\n".format(avg_rmse))
model.fit(X_data, y_target)
coeff = pd.Series(model.coef_, index=columns)
colname="alpha="+str(param)
coeff_df[colname] = coeff
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3, 6)
sns.barplot(x=coeff.values, y=coeff.index, ax=axs[pos])
if visualize == False:
plt.close()
return rmses
보스턴 집값 데이터를 사용하기 위해
보스턴 데이터 함수 정의
def get_boston_Xy():
boston = load_boston()
df = pd.DataFrame(data=boston.data, columns=boston.feature_names)
df["PRICE"] = boston.target
df.head()
X = df.iloc[:,:-1]
y = df.iloc[:, -1]
return X, y
입력한 method에 따라 변환 하는 데이터 변환 함수 정의
def get_scaled_data(method=None, input_data=None):
if method == "Standard":
scaled_data = StandardScaler().fit_transform(input_data)
elif method == "MinMax":
scaled_data = MinMaxScaler().fit_transform(input_data)
elif method == "Log":
scaled_data = np.log1p(input_data)
else:
scaled_data = input_data
return scaled_data
데이터 변환 방법과 alpha 값에 따른 rmse 비교 데이터 프레임 반환 함수 정의
def comparision_data_transform(model_name=None, X_data=None, y_target=None, alphas=None):
scale_methods = ["Standard", "MinMax", "Log", None]
df_columns = alphas.copy()
df_columns.insert(0, "scaled_method")
print("df_columns ", df_columns)
df = pd.DataFrame(columns=df_columns)
for scale_method in scale_methods:
scaled_data = get_scaled_data(method=scale_method, input_data=X)
print("# scale method = {}#".format(scale_method))
print("----------------------")
#print(scaled_data)
rmses = get_linear_reg_eval(model_name, params=alphas, X_data=scaled_data, y_target=y, columns=X.columns)
rmses.insert(0, scale_method)
rmse_series = pd.Series(rmses, index=df_columns)
df = df.append(rmse_series.to_frame().T)
return df
실행 코드
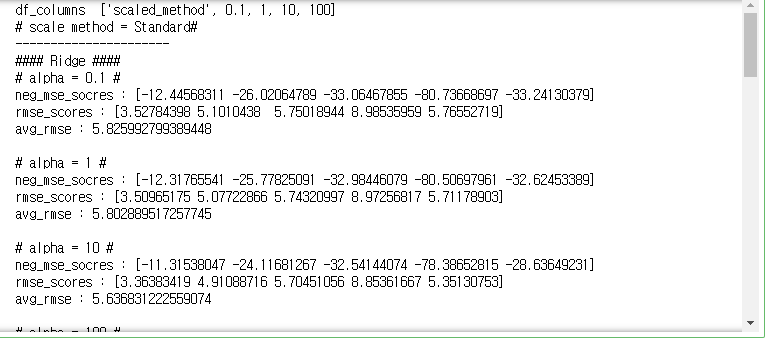
X, y = get_boston_Xy()
alphas = [0.1, 1, 10, 100]
model_name = "Ridge"
df = comparision_data_transform(model_name=model_name, X_data=X, y_target=y, alphas=alphas)
결과
- 대부분 Log 변환을 하였을때 좋은 성능을 보였음.
- Log 변환을 수행하고, 알파 값이 1일때 rmse가 4.67623으로 최적의 결과를 얻음

300x250
'인공지능' 카테고리의 다른 글
| 파이썬머신러닝 - 25. 트리기반 회귀분석 (0) | 2020.12.08 |
|---|---|
| 파이썬머신러닝 - 24. 로지스틱 회귀 분석 (0) | 2020.12.07 |
| 파이썬머신러닝 - 22. 회귀 계수 크기를 제한하기(과적합 방지) 위한 L2규제와 L1규제 (0) | 2020.12.07 |
| 파이썬머신러닝 - 21. 다항 회귀 과소 적합과 과적합 문제 (0) | 2020.12.07 |
| 파이썬머신러닝 - 20. 다항 회귀 (0) | 2020.12.06 |