728x90
다항 회귀의 문제에서
과소 적합과 과적합 문제를 다뤄보자
구간이 [0, 1]사이에
구하고자 하는 함수로 y = cos( 1.5 * pi * x)가 있다고 하자
노이즈가 추가 된 cos( 1.5 * pi * x) + N(0, 0.1)으로 부터 샘플 값을 얻을때
이 때 1차 다항식, 4차 다항식, 15차 다항식의 결과를 비교해보자
우선 필요한 라이브러리들을 가져오고
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
import warnings
warnings.filterwarnings("ignore")
%load_ext autotime
실제 함수와 샘플들, 노이즈를 추가한 y값들을 얻자
def true_func(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples))
y = true_func(X) + np.random.randn(n_samples) * 0.1
print(y.shape)
차수가 1, 4, 15인 경우에 대해
pipeline으로 학습 과정을 수행하였고,
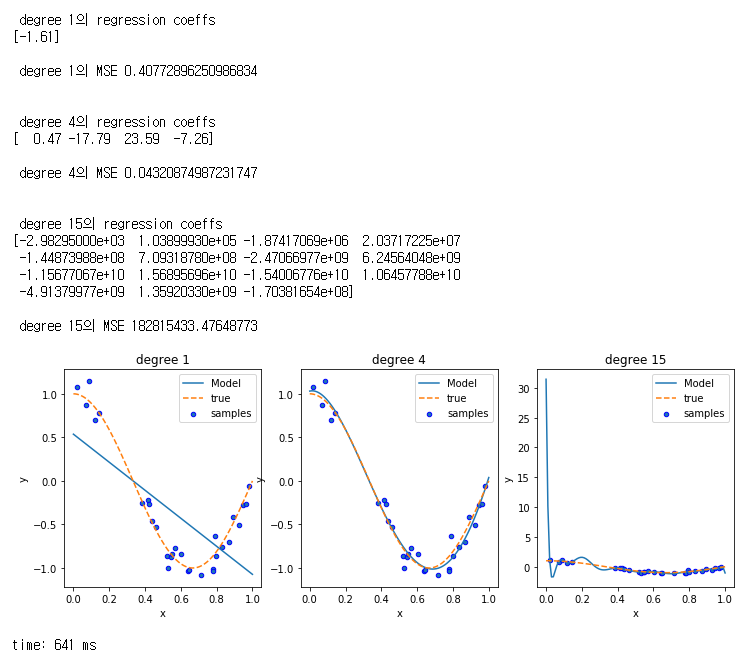
계수와 MSE를 출력해보면
fig = plt.figure(figsize=(12,4))
degrees = [1, 4, 15]
for i in range(len(degrees)):
ax = fig.add_subplot(1, len(degrees), i+1)
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X.reshape(-1, 1), y)
scores = cross_val_score(pipeline, X.reshape(-1, 1), y,scoring="neg_mean_squared_error", cv =10)
coeffs = pipeline.named_steps["linear_regression"].coef_
print("\n\n degree {}의 regression coeffs\n{}".format(degrees[i], np.round(coeffs, 2)))
print("\n degree {}의 MSE {}".format(degrees[i], -1 * np.mean(scores)))
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:,np.newaxis]), label="Model")
plt.plot(X_test, true_func(X_test),"--", label="true")
plt.scatter(X, y, edgecolors="b", s=20, label="samples")
plt.title("degree {}".format(degrees[i]))
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
4차 다항식의 경우 MSE가 가장 적으며,
주어진 샘플 데이터로 실제 다항 함수를 잘 적합한 것을 확인할 수 있다.
차수가 1인 경우 구한 선형 식에서는 너무 일반화되어 단순하며,
차수가 15에는 학습 데이터에 너무 치중한 나머지 실제와는 완전히 다른 곡선이 만들어짐.
300x250
'인공지능' 카테고리의 다른 글
| 파이썬머신러닝 - 23. 선형 회귀 모델 데이터 변환 (0) | 2020.12.07 |
|---|---|
| 파이썬머신러닝 - 22. 회귀 계수 크기를 제한하기(과적합 방지) 위한 L2규제와 L1규제 (0) | 2020.12.07 |
| 파이썬머신러닝 - 20. 다항 회귀 (0) | 2020.12.06 |
| 파이썬머신러닝 - 19. 선형 회귀 모델과 선형 회귀를 이용한 보스턴 주택 가격 예측 (0) | 2020.12.04 |
| 파이썬머신러닝 - 18. 선형 회귀 모델과 경사 하강 법 이론과 구현 (0) | 2020.12.03 |