ref : towardsdatascience.com/lines-detection-with-hough-transform-84020b3b1549
허프 변환 Hough Transform
- 파울 V.C 허프가 1962년 사진에 존재하는 직선들을 찾아내기 위해 제안한 알고리즘.
- 허프 변환은 컴퓨터 비전 분야에서 직선이나 원 같은 특징을 검출할때 주로 사용.
- 에지 영상(주로 케니 에지)에서 허프 변환을 통해 허프 공간(a, b 공간 표현법: 아래에서 후술)상의 교점을 구함.
- 허프 공간의 교점은 xy 공간에서 직선으로 표현됨
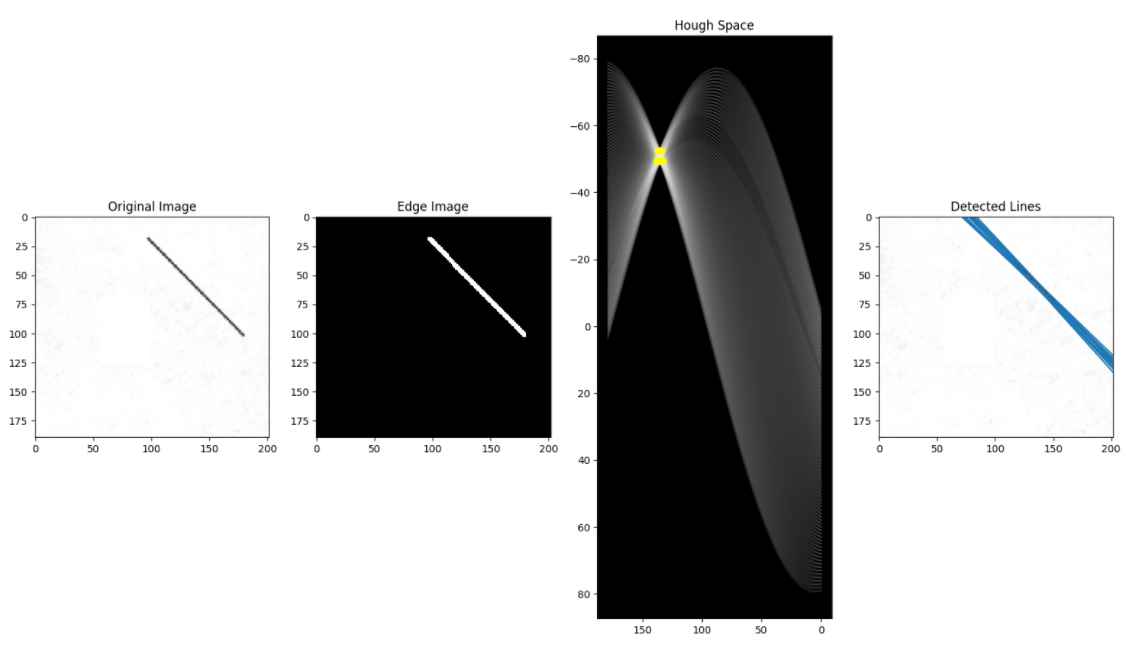
기본 허프 변환
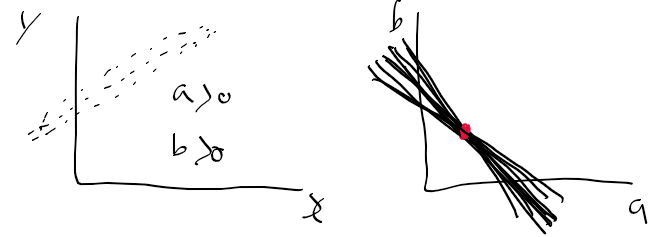
- 기존의 이미지는 x-y 평면 상에서 표현됨
- 위에서 말한 a, b 공간은 a(기울기), b(y 절편)로 이루어진 공간을 말함.
- x, y 공간에서 한 점은, ab 공간(허프 공간)에서 한 직선으로 표현할 수 있음.
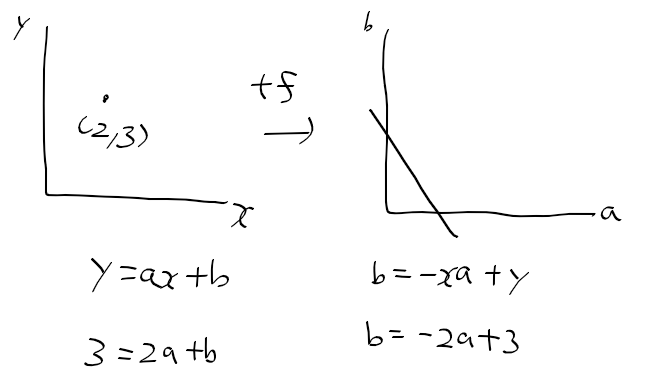
- xy 공간 상에 점이 하나 더 생기면 a-b 공간상의 교점이 생긴다.
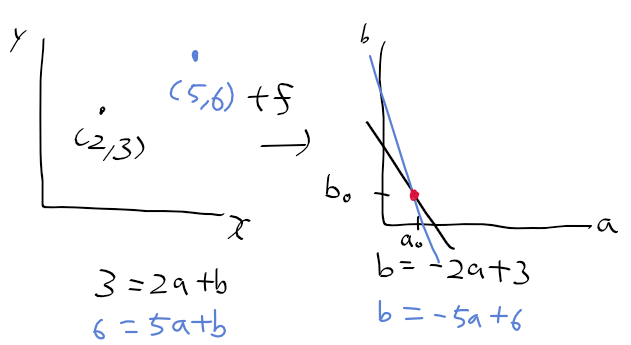
- a-b 공간 상의 교점이 두 점이 지나는 직선의 기울기와 y 절편 값이 된다.
=> 이렇게 하여 ab 표현을 이용한 직선 검출이 수행.
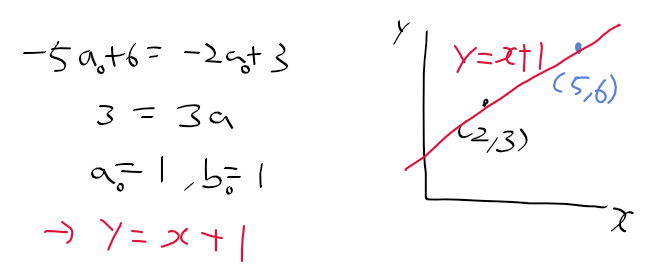
ab 공간의 문제
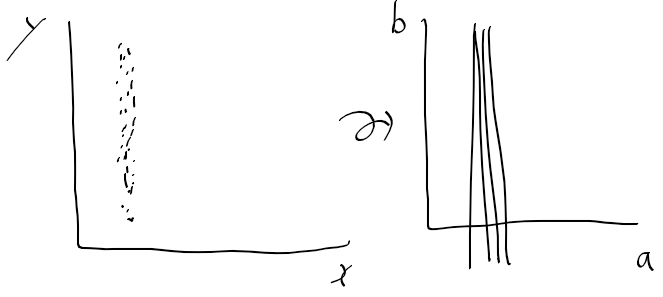
- 아래의 좌측과 같은 에지 영상이 주어지면, 이들은 대부분 ab 공간 상에서 하나의 교점에서 만날것임
- 하지만 에지가 수직인 경우, ab 공간에서 b가 무한대가 되버리는 문제 발생
-> 대안으로 rho, phi를 이용한 법선 normal line 표현법을 사용함.
* 법선 normal line : 곡선의 한 점을 지나며, 접선에 수직인 직선
법선을 이용한 허프 변환
- 두 점을 지나는 법선은 원점까지 수직인 거리가 rho, 이때 각을 phi로 표현
- 수직 거리 rho, 각도 phi의 관계 : rho = x cos(phi) + y sin(phi)
- 하단의 우측 그림처럼 이전과 마찬가지로 rho, phi 공간 상에서 교점이 xy 공간상에서 직선을 의미함.
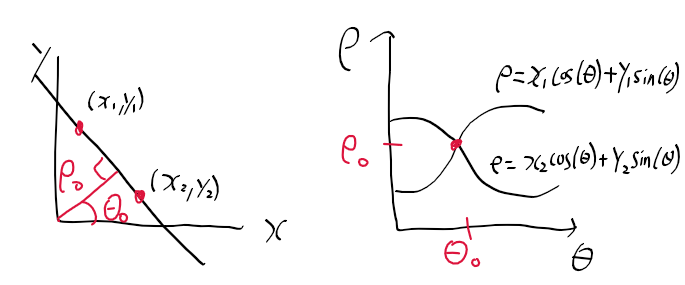
- ab 공간떄와는 달리 에지가 수직 혹은 수평의 형태인 경우에도 rho나 phi가 무한대로 발산하지 않음.
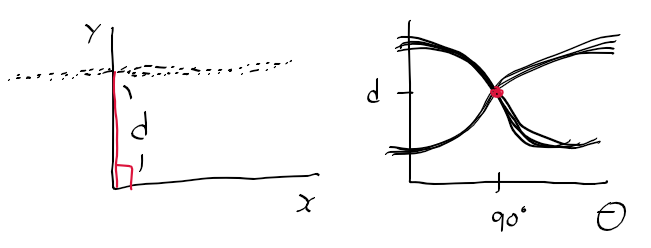
정리한 내용은 얼마 안되는데 시간이 너무 늦어졌다...
구현은 내일로
'로봇 > 영상' 카테고리의 다른 글
| 컴퓨터 비전 알고리즘 구현 - 13. 행렬 연산을 이용한 허프라인 구하기 (0) | 2020.12.06 |
|---|---|
| 컴퓨터 비전 알고리즘 구현 - 12. 허프 변환을 이용한 직선 검출 구현 (0) | 2020.12.05 |
| 컴퓨터 비전 알고리즘 구현 - 10. 캐니 에지 검출기 만들기 (0) | 2020.12.01 |
| 컴퓨터 비전 알고리즘 구현 - 9. 이미지 그라디언트 (0) | 2020.11.30 |
| 컴퓨터 비전 알고리즘 구현 - 8. 모폴로지 연산 (0) | 2020.11.30 |