michigan online justin johnson
deep learning for computer vision
Training Neural Networks Part 2

이제 11번째 강의를 할 차례고 오늘 배울 내용은 몇가지 핵심적인 팁들과 신경망을 학습하는데 필요한 기법들에 대해서 배워보도록 합시다.
우선 이번 강의에서 더 나은 제목을 만들지 못해서 일단 사과를 하고, 지난 강의에서는 신경망을 학습을 할때 필요한 다양한 방법들을 살펴봤었습니다. 하지만 어떻게 해야 좋은 타이틀을 만들지가 어려웠습니다.

아무튼 이번 강의에서는 여러분들이 신경망을학습하는데 알아야할 것으로 약간 다른 주제의 중요한 것들을 다루려고 합니다. 지난 시간에는 one-time setup 그러니까 신경망 아키텍처에서 시작 설정을 어떻게 할지에 대해 위주로 살펴봤는데 학습을 시작하기전에 해야될 것들을 배웠다고 할수 있겠습니다.

그래서 아주 다양한 활성화 함수들에 대해서 살펴봤었고, 왠만한경우 ReLU를 사용하기로 정리하였습니다.

그리고 데이터 전처리에 대해서도 이야기 했지만, 데이터 전처리에 관한 미스터리들은 과제를 하면서 이해할수 있었을거에요.

그리고 다음으로는 자비에 같은 초기화 방법들을 사용해서 어떻게 활성화 함수를 초기화 시킬지 신경망 각 계층마다 좋은 분포로 나올수있도록 하는 것에 대해서 살펴봤구요. 그 과정에서는 출력 결과가 너무 작아 0에 가까워지거나 혹은 너무커서 1이나 -1로 극단적으로 되거나 하는 문제 사이에서 어떻게 이걸 트레이드 오프/궤환관계/조정을 해나갈지에 대한것들을 볼수 있었습니다.

그리고 지난 시간에 데이터 증강에 대해서 이야기했는데, 기존 훈련 셋을 신경망에 학습 시키기전에 훈련 데이터셋을 임의의 변환들을 적용해서 훈련 셋의 크기를 여러배로 늘리는 방법을 말한다고 했었습니다. 그리고 데이터 증강 방법을 고를때 우리가 어떤 문제를 다룰것인지에 따라 다른 데이터 증강 기법을 사용해서 신경망 훈련 과정에 사용하였습니다.

그리고 우리는 규제에 대한 일반적인 개념들을 봤었는데, 과제물에서 l2 같은 규제가 규제항을 추가하여 사용해보았을겁니다. 이 규제항은 비용 함수에 추가되어 패널티를 주는데 L2 규제의 경우 가중치 행렬의 노름 norm을 사용하였었구요.
하지만 지난 시간에는 신경망에서 자주 사용되는 더 일반화시킨 규제기, 규제 역활을하는 방법에 대해서 봤었는데 이 방법에서는 신경망의 순전파 처리과정에 랜덤성 같은 노이즈를 주고, 테스트 과정에서 노이즈/랜덤성에 대해 주변화를 한다거나 평균을 구하는 과정이 규제의 일반화 된 패턴인 것으로 알 수 있었습니다.
위 그림에서 다양한 규제 방법들의 예시를 볼 수 있는데, 우리는 드롭 아웃이나 프랙탈 풀링, 드롭 커낵스, 확률적 깊이 방법이나, 실제로는 잘 사용되지는 않지만 컷아웃이나 믹스업 같은 특이한 방법도 알아봤었어요. 아무튼 규제에 대해서는 여기까지 봤고, 이제 다음 배울 내용으로 넘어갑시다.

지금까지는 지난 시간에 배운 내용들을 살펴봤고, 오늘은 어떻게 신경망을 학습시킬것인가에 대한 다른 중요한 주제들에 대해서 배워봅시다. 특히 이번에 이야기하고자 하는건 모델을 훈련 시킬때 조심할 필요가 있는데, 모델이 학습할수 있도록 하기 위해선 학습률 스케줄 learning rate schedule을 설정하고, 어떻게 하이퍼 파라미터를 선정할지를 잘 고려애야 합니다.
이 과정이 엄청 힘든건 알지만, 그 이후에 우리가 추가적으로 고려해야 할 사항들은 학습을 잘 마친 이후인데, 우리 모델을 어떻게 할지에 대해섭니다. 모델 앙상블을 할수도 있고, 전이 학습을 할 수도 있고, 그리고 만든 모델을 스케일 업, 더 키워서 어떻게 전체 데이터센터 레벨에서 계산을할지 등을 학습한 이후에 고려해야 합니다.

우선 가장 먼저 다룰 주제는 학습률 스케쥴 learning rate schedules인데

이전에 다양한 최적화 알고리즘을 봤었었죠. 바닐라 SGD나 SGD + 모멘텀, Adagrad, RMSProp, Adam 같은 것들이요. 그리고 이 모든 최적화 알고리즘들은 학습률 learning rate라고 부르는 하이퍼 파라미터를 가지고 있었어요. 보통 이 학습률 하이퍼 파라미터는 심층 신경망 모델을 설정하는데 있어서 필요한 가장 중요한 하이퍼 파라미터라고 할수 있습니다.
지금까지는 다양한 모델들에다가 SGD를 사용을 했었다보니, 다른 최적화기에다가 다른 학습률을 사용했을때 어떤일이 일어날지 아마 감이 잡히기 시작할건데, 일단 위의 왼쪽 그림으로 다양한 학습율을 지정했을때 최적화가 어떻게 되는지 보여주고 있다.
이 그림에서 노란색 예시는 학습율을 너무 높게 지정한 경우로 바로 폭증해 버려 무한대로 가게 된다. 그래서 아주 빠르게 잘못되는 경우라고 볼수 있다. 반대로 파란색 같은 경우에는 학습률을 아주 작게설정한 경우로 학습하는 과정이 매우 느리게 진행된다. 이렇게 학습률을 설정한느건 비용이 무한대로 폭증하지는 않아 좋을수는 있지만, 학습하는 과정에서 비용이 떨어지도록 하는데 오랜 시간이 걸리게 된다.
이번에 녹색선의 경우 학습률이 높기는하나 너무 싶하기 크지는 않은 경우로 다행이 비용이 무한대로 폭증하지는 않는다. 파란색 학습률보다 높게 설정한 덕분에 더 빠르게 최저점으로 수렴을 할수있으나 비용이 최소가 되는 지점으로 확실하게 수렴한다고는 할수 없는 문제가 있다.
마지막으로 빨간색 곡선의 경우 가장 이상적인 학습률로 비용이 최소가 되는 지점으로 빠르게 수렴하며, 무한대로 폭증하지 않고, 학습 과정이 꽤 빠르게 진행된다. 그래서 빨간색 곡선과 같은 학습률을 찾는게 좋겠다.

하지만 빨간색 커브처럼 좋은 학습률을 찾지 못하는 경우도 있는데, 이런 완벽한 학습률을 찾을수 없을때는 위의 질문 처럼 우리는 어떻게 해야할까? 어떻게 위 그림에서 보이는 차선의 학습률들 사이에서 트레이드 오프를 잘 고려해서 선택해야한다고 한다면

위 질문에서는 사용하기 가장 좋은 학습률이 어떤 것인가를 묻고 있으나 이 질문을 조금 비틀어서 보면, 꼭 다양한 학습률중에서는 한가지만 사용해볼 필요 없이 모두 사용해보면 된다.
예를 들자면 상대적으로 학습률이 큰 경우에서 시작해서 녹색 곡선같은, 그러면 비용은 첫 학습 에폭에서는 비용이 어느 정도 낮은 지점까지 떨어지고 나서 시간이 흐르면 녹색 커브는 평평하게 된다.
파란색 곡선처럼 학습률이 낮은 경우를 생각하면 결국에는 비용이 가장 최저가 되는 지점을 찾을수 있을거다. 그래서 높은 학습률에서 시작하고 시간이 지나면서 학습률을 낮추면, 시작 당시에는 빠르게 진행하고 학습 끝에는 비용이 아주 작은 지점으로 수렴할수 있게 된다.
하지만 지금까지 이야기 했던 것들은 명확하지 않고 애매하게 이야기를 했는데, 지금까지 큰 학습률로 시작하고 나중에는 낮은 학습률을 사용한다고 했지만 이 과정을 어떻게 구체적으로 표현할 수 있을까?
조금 더 구체적으로 이야기 하자면 학습 과정에 학습률을 바꿔가는 메카니즘을 골라서 처리하는 과정을 학습률 스케쥴이라고 한다. 이 학습률 스케쥴에는 여러가지가 있는데 심층 신경망 모델을 학습하는데 자주 사용되고 있다.

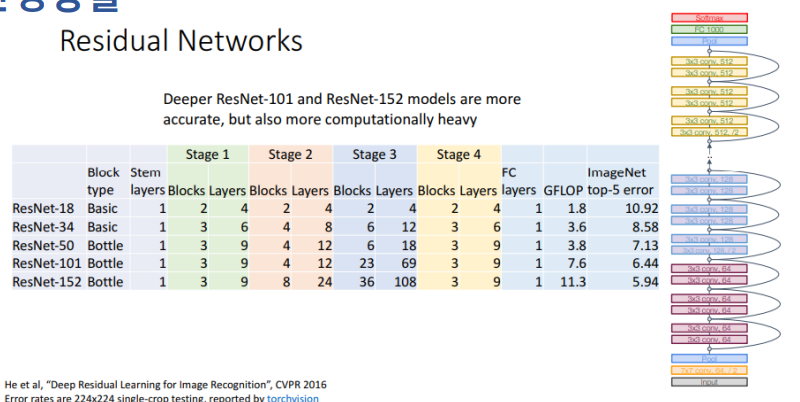
가장 많이 사용되는 학습률 스케줄 방법으로 스텝 스케줄이 있다. 위 예시에서 여러가지 학습률 값들이 있는데 ResNet에서 이런 스텝 학습률 스캐줄이 잘 사용되고 있다. 이런 학습률 스케쥴을 가지고 처음에는 상대적으로 큰 학습률 0.1로 시작하였다가 최적화 가정에서 특정 지점에서 학습률을 감쇄시키고자 더 낮은 학습률을 사용한다.
그래서 ResNet에서 학습률 스케줄은 처음에는 0.1에서 시작하고 30 에폭에서 학습률을 0.01로 낮추어 학습을하고, 60에폭에는 더 크게 떨어트리고 90에폭에서는 더 떨어트리는 식으로 학습이 진행된다. 일반적으로 훈련 중 30 에폭마다 학습률을 1/10의 비율로 떨어트린다.
위의 왼쪽 그림은 학습률 감쇄 스케쥴이라고 부르는 건데, 여기서 비용 함수의 특성이 나타나는 곡선을 볼수 있다. 여기서 스텝 학습률 감쇠로 첫 30 에폭 페이스에선 상대적으로 큰 학습률을 사용해서 빠르게 진행을 하여, 큰 값으로 시작했던 초기 비용을 지수적으로 줄일수가 있었다.
하지만 30 에폭쯤에서 처음 처럼 빠르게 진행할 수가 없어, 이 30에폭 시점에서 학습률을 감쇄시켜 10으로 나눈뒤 학습을하면 다시 비용이 급격히 떨어져 지수적인 패턴이 나오기 시작한다. 또 다시 평탄한 부분이 나오면 60 에폭 쯤에서 학습률을 다시 감쇄하여 빠르게 떨어트리고 다시 평탄해지는 스케줄을 사용하였을때 이런 특성이 나타나게 된다. 이게 스탭 학습률 스캐쥴이란 방법으로 모델을 학습시킬때 볼수 있는 학습률 곡선의 특성 형태가 되겠다.
이런 스탭 학습률 스케쥴을 사용할때 문제가 있는데, 모델을 학습하는데 여러개의 하이퍼 파라미터가 필요하다. 지금까지는 우리는 어떤 규제를 할지, 지금까지 모델을 학습할때 사용했던 초기 학습율을 고를지를 고려했으나 그 뿐만이아니라 어디 쯤, 어느 에폭에서 학습률 감쇄를 할지도 골라야 한다.
그렇다보니 스텝 감쇄 스캐쥴의 경유 튜닝하는데 워낙 많은 경우의 수가 있다보니 꽤 많은 시행착오가 필요하다. 사람들이 주로 학습률 커브를 설정하는 방식은 비용이 평평한 지점을 찾도록 꽤 오랫동안 큰 학습률로 학습을 시키는 것으로 한번 다른 논문들을 살펴본다면 다들 경험적인 방법을 사용했다고 하는데 비용이 평평한 지점이 나올떄까지 혹은 검증 정확도가 평탄해질떄까지 그대로 유지시키다가 학습률을 감쇄시키며 경험적으로 감쇄 스캐줄을 할 스탭을 선정하였다.
하지만 이렇게 하는것의 문제는 다양한 감쇄 스케줄을 실험해볼 시간이 충분하지 않다는 점은데, 그래서 이 스탭 감쇄 스케쥴은 튜닝해야할 부분들이 너무 많다보니 이 사용하기 좀 까다로운 문제가 있다.

그래서 스탭 감쇄 스케줄의 단점을 극복한 다른 학습률 스캐줄 방법으로 최근 몇년간 트랜드로 사용되고 있는걸로 코사인 학습률 감쇄 스케줄이 있다. 이 방법에서는 이전 처럼 특정 반복 회차, 에폭에서 감쇄하는게 아니라 시간에 대한 함수를 사용하는데, 학습률은 모든 에폭 회차에 대한 함수로 정해집니다. 그래서 여기서 할일은 학습률을 어떻게 감쇄시킬지를 나타내는 곡선 형태의 함수가 있으면 되요.
이 중에서 가장 대표적인것으로 코사인으로 하프 코사인 학습률 스캐쥴러가 있으며 오른쪽과 같습니다. 여기서 학습률은 시간에 대한 함수로 처음에는 아주 큰 값으로 시작하고, 학습률 감쇄는 코사인파의 절반과 같은 형태로 정해지게 되요.
그래서 처음에는 학습률이 높이 시작했다가 학습이 끝날떄 쯤에 핛습률이 감쇄되서 0에 가까워 지게 됩니다. 이 ㅋ코사인 학습률 감쇄 스캐줄은 파라미터가 2개 뿐인데, 초기 학습률로 사용할 $\alpha_{0}$와 다른 하나는 학습할 에폭의 수로 T로 표기합니다.
이 코사인 학습률 스케쥴에서는 초기 학습률과 에폭 수만 필요하지, 이전에 봤던 다른 하이퍼 파라미터가 필요하지 않습니다. 그래서 코사인 스캐줄러는 이전에 본 스탭 감쇄 스캐줄러보다 다루기가 쉬우며, 일반적으로 학습을 길게 할수록 잘 동작하는 경향을 보여요.
우리가 할 일은 초기 학습률과 모델이 얼마나 오래 학습시킬지만 튜닝하면 되겠습니다. 그래서 이런 이유들 덕분에 코사인 학습률 스캐줄러가 최근 몇년간 가장 많이 사용되었다고 볼수 있겠습니다. 그리고 위 슬라이드 아래 부분에다가 최근 몇 년간 코사인 러닝 스케줄이 사용된 논문들을 짚어넣었습니다.

하지만 코사인은 시간 변화에 따른 학습률 감쇄에 사용할수 있는 수많은 형태중 하나이고, 다른 감쇄 스케줄로 사람들이 종종 쓰는걸로 단순 선형 감쇄도 있습니다. 일정한 초기 학습률로 시작해서 학습 과정을 거쳐 0까지 감쇄가 되요. 하지만 코사인 감쇄보다 이 감쇄 학습 스케쥴은 학습률을 시간에 따라 선형적으로 간단하게 감쇠를 해요.
그리고 많은 문제에서 잘 동작을 하는데, 짚고 넘어갈 점은 다른 스케줄링 기법이랑 비교해서 잘되는지에 대한 좋은 연구들이 없습니다. 그래서 코사인 학습률 스캐줄러가 좋은지 선형 학습률 스캐줄러가 좋은지 확실하게 말하기는 어렵습니다.
제 생각에 대부분의 사람들이 실제로 사용하는 방법은 사전에 있었던 연구가 어떤 타입의 스케쥴을 사용했던지 상관없이 참고해서 사용합니다. 이게 무슨 말이냐면 여러 딥러닝 분야에 따라 다른 학습률 스캐줄 방법을 사용하는 경향이 있는걸 보게 될게 되요.
=> 정리가 매끄럽지가 않은데 다시 정리하면
학습률 스캐줄러를 정하기 위해서 관련된 사전 연규에서 사용한 학습률 스캐줄러를 사용함.
그래서 특정 문제에서 비슷한 학습률 스캐줄러가 자주 사용되는 경향을 보임
하지만 한 분야, 특정 분야에서에서 그 학습률 스캐줄러가 좋아서 그렇게 사용했다고 하기보다는, 저의 생각에서는 이전 연구에서 있었던것과 비교하기 위해서 그렇게 한다고 생각됩니다.
-> 이전 연구에서 사용한 학습률 스캐줄러를 쓰는건 그 스캐줄러가 해당 분야에서 성능이 다른것 보다 좋아서라기 보다는 이전 연구와 비교하기 위함.
우리가 이전 연구를 보면서 명심해야할건 우리가 다룰 컴퓨터 비전의 문제에 따라서 어떤 경우 코사인 학습률 감쇄 스캐줄을 사용할수도 있고, 아주 큰 스캐일의 자연어 처리를 다루는 경우에는 선형 학습률 스캐줄을 사용할수도 있습니다.
이 학습률 스캐줄링은 비전이랑 자연어에 대한 근본적인것은 아니지만 서로 다른 분야의 연구자들이 연구해온 방향대로 사용하면 되겠습니다.

이번에 또 다른 학습률 스캐줄러로 역 제곱 루트 스케줄러가 있는데, 아주 큰 학습률로 시작해서 작은 학습률로 끝나게 되는데, 이 방식은 2017년에 아주 주목을 받던 논문에서 사용하던거라 추가하였습니다. 하지만 선형 감쇄 스캐줄이나 코사인 감쇄 스캐줄과 비교해서 사용되는갈 자주보지는 못했어요.
제 생각에는 역 제곱근 스캐줄러가 가지는 잠제적인 위험은 아주 높은 학습률을 사용하는 시간이 아주 짧기 때문이라고 봅니다. 여러분도 이 학습률이 아주 큰 초기값으로 시작하지만 급격히 떨어지고 대부분의 시간을 아주 낮은 학습률로 학습을 하게되는걸 볼수 있어요.
그래서 이걸 선형이나 코사인학습률 스캐줄과 비교해본다면, 다른 학습률 스캐줄러는 초기에 아주 높은 학습률이 더 오랜 시간동안 사용되는걸 볼 수 있어요.

지금까지 본 학습률 스캐줄과 다른 이번에는 실제로 아주 많이 사용되는 학습률 스케줄링 방식은 상수 스캐줄 입니다. 이건 아주 많은 문제들에서 실제로도 잘 동작을 하는데, 우리가 알다시피 그냥 초기 학습률을 지정하면 그 학습률로 전체 학습 과정에서 쭉 학습을 하는거에요.
이 방식을 다른 걸쓸 이유가 없다면 실제로 쓰는걸 추천하는데, 사람들이 딥러닝 프로젝트를 시작할때 이 학습률 스캐줄을 가지고 오랜시간 해매는걸 봤었고, 이 학습률 스캐줄을 조정해나가는게 모델을 개발하고 동작하는데 필요한 일인데, 상수 시간 학습률 스캐줄을 사용하면 꽤 좋은 결과를 얻을수 있어요.
상수 학습률 스캐줄과 다른 복잡한 스캐줄을 사용했을때 모델이 동작하느냐, 안하느냐에서 일반적으로 차이는 없고 대신 상수 스캐줄에서 복잡한 스캐줄로 바꿀때 성능이 몇 퍼센트 정도 더 좋아집니다. 그래서 어는 문제에 대한 기술을 다룰 뿐만이 아니라 목표가 해매는 일 없이 빠르게 돌려보고 있다면, 상수 시간 학습률이 꽤 좋을 수 있겠습니다.
여기서 학습률과 최적화기 사이에 대해서 더 이야기 할게 있는데, 확률적 경사하강 + 모멘텀을 사용할때 어떤 학습률 감쇄 스캐줄을 사용할 것인지가 중요할 수도 있습니다. 하지만 RMSProp나 Adam같은 복잡한 최적화기를 사용하는 경우라면 상수 시간 학습률 스캐줄만 사용해도 됩니다.(이전에 최적화에 대한 강의에서 RMSProp, Adagrad 등의 방법에서 학습률을 최적화기가 조정했던 것으로 기억)
다음 주제로 넘어가기 전에 학습률 스캐줄에 대한 질문들을 보면, 여러분들은 오랜 시간 동안 학습을 해서 비용이 쭉 내려가면 아주 좋겠죠. 여러분들이 만든 모델이 좋은 모델이니까. 그런데 비용이 갑자기 증가해버린다면 실망할겁니다. 하지만 이런 일이 있을때 일반화시켜서 말하기가 힘드는데, 잘못 동작하도록 해서 이런 문제가 생기는 원인이 많으니까요.
한가지 경우는 중간에 그라디언트가 0이 되는 경우가 있어서 그럴수도 있는데, 이 문제가 아니라 그라디언트가 여러번 반복하는과정에서 너무 누적되서 급격히 커지는 경우가 생기면 학습이 잘못 될겁니다. 또, 우리가 다루는 문제의 타입에 따라 잘못된 학습 과정으로도 이런 문제가 생길수도 있구요. 다른 종류의 생성모델이나 다른 종류의 강화학습 문제를 다루다가 학습 커브가 잘못되는걸 볼 수도 있겠습니다.
우리가 잘 정리된 분류 문제를 다룬다고 해도, 일정 기간 학습을 한 후에 비용이 급격히 커지는 일이 생긴다면, 나쁜 하이퍼 파라미터를 써서 버그가 생긴걸 수도 있고, 데이터가 로드 되는 과정에서 버그가 생겼거나, 훼손된 데이터를 가지고 학습을 시켜서 생깃 것으로 추정할 수도 있겠습니다.
그리고 우리가 가진 데이터셋에 한 샘플이 잘못된 경우도 문제의 원인이 될수도 있고, 다른 문제가 생길수 있는 경우로 여러분들이 Flickr를 알고 있으면 사용자들이 Flickr나 다른 사진 공유 사이트에 올릴수 있을거에요. 그리고 후에 이 사진들을 삭제를 할수도 있겟죠.
Flickr 이미지 배포 링크로 실제 JPEG이미지들을 모아 데이터셋을 만들수도 있는데, 그 중간에 이미 삭제된 이미지를 다운로드 하려고 할수도 있을거에요. 그래서 실제 이미지가 아닌 손상된 JPEG 파일/실제 내용은 없고 텅빈 이미지 파일을 다운받을 수도 있고, 훈련하는 과정에서 사용하면 그 이미지는 라벨은 가지고 있으나 0인 데이터가 될수도 있어 비용을 급격하게 증가시킬수도 있겠습니다.
그래서 여러분이 이런 손상된 이미지들을 포함한 미니패치를 가지고 학습을 하려고해서 갑자기 이런 문제를 발생시킬수도 있어요. 그래서 일반화 시켜서 대답하기는 힘들고 여러분들의 문제가 뭐가 원인인지 깊게 들여다봐야 합니다.
다음 질문은 적응적 학습률에 관한 것으로 Adadgrad나 RMSprop 혹은 다른 적응적 학습률 방법이 있는데, 이들도 문제를 발생시킬수도 있지만 이 방법들은 더 강인하게 만들어지다보니 그래도 최적화 문제에서 계속 사용해도 되갰습니다.
*이후 몇가지 질문에 대해서 더 얘기하지만 학습률 스캐줄에 관해서는 여기까지..

훈련을 얼마나 지속시킬지 결정하는데 도움되는 것으로 빠른 중지early stopping이라고 하는 개념이 있습니다. 이전에 신경망을 학습하면서 주로 세가지 커브를 보았는데, 하나는 좌측의 비용에 대한 그래프로 정상적으로 동작하면 지수적으로 감쇄되는걸 볼수 있어요. 그리고 꼭 봐야하는것으로 신경망의 훈련 정확도인데, 매 애폭마다 채크를 해줘야하고, 훈련셋에 대한 정확도 뿐만이 아니라 검증셋에 대한 정확도도 확인해주어야 합니다.
이 곡선들을 보면서 만든 신경망이 학습 과정에서 정상적으로 동작하는지 알수 있어요. 일반적으로 우리가 할수 있는건 검증 정확도가 가장 높은 지점에서 학습을 중지시킬수가 있겠습니다. 그리고 그리고 그 지점을 최대 반복 회수 최대 에폭으로 지정해서 훈련을 할수 있을것이고, 매 애폭마다 배치단위들을 학습할수가 있겠습니다.
하지만 모든 에폭 혹은 모든 5에폭 단위 혹은 10 에폭씩 훈련셋과 검증셋 정확도를 확인해야하고, 각 지점에서 모델 파라미터들을 저장을 해두어야 합니다. 모델이 핛브을 마친 후에 이러한 곡선들을 그릴 수 있고, 가장 검증셋의 성능이 좋은 시점에서의 지점을 고르면 되겠습니다. 그 체크포인트에서의 모델을 실제로 사용하겠습니다.
이런 식으로 모델을 돌리는 중간에 훈련 과정에서 비용이 뒤에 갑자기 증가하는 경우도 생기는데, 이건 큰 문제가 되지 않고, 그냥 커브를 보고 갑자기 증가하기 이전에 있는 것들 중에서 가장 적합한 체크포인트의 모델을 사용하면 되겠습니다.
이 방법은 신경망을 어떻게 학습시킬지 어디까지 학습시킬지 고르는데 매우 유용한 경험적인 방법이라고 할 수 있겠습니다. 그리고 이걸 신경망을 학습할떄시킬떄마다 사용하라고 추천드리고 싶습니다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 3. 학습 후 할 수 있는 일 (0) | 2021.03.07 |
|---|---|
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 2. 하이퍼 파라미터 찾기 choose hyperparameter (0) | 2021.03.06 |
| 딥러닝비전 10. 신경망 학습하기 파트 1 - 4 규제 기법 (0) | 2021.02.26 |
| 딥러닝비전 10. 신경망 학습하기 파트 1 - 3. 가중치 초기화 2 (0) | 2021.02.25 |
| 딥러닝비전 10. 신경망 학습하기 파트 1 - 3. 가중치 초기화 1(대칭 깨짐) (0) | 2021.02.23 |