
그 다음으로 우리가 자세히 다뤄야할 주제로 신경망에서 사용할 하이퍼 파라미터를 어떻게 선정할까인데

흔히 볼수있는 대표적인 방법으로 그리드 탐색 grid search가 있겠다. 여기서는 하이퍼 파라미터의 집합이 있는데 각각의 하이퍼파라미터들을 사용하면서 선택한 하이퍼파라미터를 사용한 결과들을 평가하는 방식이다.
어쩔때는 선형 공간, 그러니까 하이퍼파라미터가 선형적으로 증가하는 경우보다 로그 선형 공간을 탐색해야하는 경우도 있다. 예를 들자면 위와 같이 4개의 로그 선형 공간상에서의 학습률과 4개의 로그 선형 공간 상에 있는 규제 강도, 가중치 감쇄치가 로그 선형 공간에서 탐색해야하는 하이퍼 파라미터인데, 이 4개의 학습률과 4개의 가중치 감쇄값으로 총 16가지 경우의 조합을 만들수가 있게 되겠다.
만약 충분한 GPU 자원이 있다면 모든 경우들을 다 돌려보고 가장 좋은 성능을 보이는 하이퍼 파라미터를 찾으면 되겠지만, 하이퍼 파라미터의 개수가 많은 경우 GPU또한 많이 필요하고 하이퍼 파라미터를 튜닝하기가 어려워 질것입니다.

그래서 그리드 탐색 대신 사람들이 사용하는 방법으로 랜덤 탐색 random search가 이용합니다. 이 방법의 경우 여러개의 하이퍼 파라미터들을 놓고 선택해서 평가하는 그리드 탐색과는 달리 하이퍼 파라미터 값의 범위를 지정해 놓고, 매 훈련 때 마다 그 범위에 속하는 랜덤한 값을 골라 하이퍼 파라미터로 사용하는 방법이다.
학습률과 가중치 감쇄 같은 하이퍼 파라미터들은 로그 선형 공간에서 탐색을 해야되겠지만 모델 사이즈나 드롭 아웃 같은 확률의 경우 로그 선형 공간 보다는 선형 공간 상에서 탐색을 해야 하는데, 이와 같이 선형 공간에서 탐색해야하는 것인지 로그 선형 공간에서 탐색해야하는지는 어떤 하이퍼 파라미터이냐에 따라 달렸다고 볼수 있겠다.
아무튼 이 랜덤 탐색 방법을 사용하는 경우 각 하이퍼 파라미터마다 각자 범위를 지정하고, 학습할때마다 구한 랜덤 값을 하이퍼 파라미터로 사용하는데, 여기서 시행 착오/학습을 반복할 횟수는 만든 신경망 모델로 여유있게 훈련 시킬수 있는 만큼 해주면 되겠다. 그렇게 학습이 끝날때까지 최고의 성능이 나온 하이퍼 파라미터로 시용하면 된다.

2010년 초반에 나온 논문에 따르면 랜덤 탐색과 그리드 탐색을 비교할때 비슷하게 동작하기는 하지만 랜덤 서치를 사용할때 더 좋은 하이퍼 파라미터를 찾을수가 있다고 한다.
-> 한 논문에 따르면 랜덤 탐색이 그리드 탐색보다 하이퍼 파라미터 탐색에 좋다.
탐색하고자 하는 하이퍼 파라미터가 많다고 할때, 어떤 하이퍼파라미터들은 모델 성능에 있어서 중요한 것들이 있을수도 있고, 그렇치 않은 값들도 있있겠다. 하지만 학습하기 전까지 어떤게 중요한 하이퍼파라미터이고, 중요하지 않은 하이퍼파라미터인지 알수는 없다.
-> 다양한 하이퍼 파라미터가 있겠지만 어떤게 중요하고, 안 중요한지 알 수 없다.
그래서 그리드 탐색을 사용한다면 위에서 왼쪽 그림에 나오는 그리드 파라미터를 직접 평가해볼수가 있겠다. 위 왼쪽 그림의 수평 축은 신경망 성능 최적화에 중요한 파라미터를 보여주는데, 이 분포는 다양한 하이퍼 파라미터가 주어질때 성능에 대한 주변 확률 분포를 의미하고 있다.
-> 중요한 하이퍼 파라미터와 중요하지 않은 하이퍼 파라미터가 두 타입이 있는 경우 주변 분포
한번 간단한 예시를 들자면 이 수평 축에서 왼쪽으로 갈수록 낮은 성능을 보이고, 중앙에서는 높은 성능을 보이다보니 이 수평 방향의 하이퍼 파라미터가 성능 향상에 중요한 하이퍼파라미터임을 알수가 있겠다.
-> 중요 파라미터의 주변 분포에 따르면 어떤 경우 성능 향상에 기여하지 않지만 어떤 경우 크게 성능이 향상.
이와 반대로 수직방향 하이퍼 파라미터는 모델 성능 개선에 크게 중요하지 않는데, 그림의 왼편에 노란색의 주변 확률 분표를 보면 이 수직 하이퍼 파라미터 값이 어떻든간에 성능에 큰 영향을 주지않는다고 볼수 있겠다.
-> 중요하지 않은 하이퍼파라미터는 어떤 값이 오든 성능 향상에 큰 변화를 주지 않음.
여기서 문제점은 그리드 탐색을 할때 매 반복때마다 중요한 타입의 파라미터를 고정 시켜 놓고, 중요하지 않은 타입의 하이퍼파라미터 값을 여러 경우로 반복하다보니 그렇게 많은 정보를 얻을수가 없으며, 이 그림의 예시의 경우 중요한 하이퍼 파라미터의 값이 3가지 인 경우에 대한 경우 밖에 볼수 없게 된다. 그렇다 보니 어떻게 튜닝하는게 좋은지 충분한 정보를 얻을수가 없다.
-> 그리드 탐색은 한 타입의 하이퍼 파라미터 값을 고정시키고 다른 타입의 값을 변화시킴. 위 예시의 경우 중요 파라미터 값이 3가지인 경우 밖에 볼수가 없다.
하지만 랜덤 탐색의 경우 매 학습/시도 때마다 수직 방향/중요하지 않은 타입값, 수평 방향/중요한 하이퍼파라미터 값을 랜덤하게 구하여 시도하므로, 하이퍼 파라미터 값의 변화에 따른 모델 성능을 주변 분포로 그린 결과(수평 방향 분포)를 같이 보면 그리드 탐색에서는 수직, 수평방향으로 정렬되어 있었다보니 정확하게 일치하지 않은 랜덤 탐색으로 보다 더 다양한 경우 결과를 얻고, 더 효과적으로 중요한 하이퍼 파라미터 값/샘플이 무엇인지 찾을수가 있겠다.
-> 그리드 탐색에서 값들이 수평, 수직방향으로 일치하다보니 중요한 하이퍼 파라미터의 값이 3가지인 경우만 볼수 있었지만 랜덤 탐색은 범위 안의 무작위 값을 사용하다보니 더 다양한 경우의 하이퍼 파라미터들을 사용할 수 있고, 더 좋은 성능을 보이는 하이퍼파라미터를 찾기 좋다.
이 슬라이드를 통해서 랜덤 탐색을 하는 예시를 살펴보았고,

이 예시는 3가지 모델을 가지고 학습률과 규제 강도를 평가한 예시인데, 순전파 모델과 잔차 모델, 그리고 DART라고 부르는 신경망 아키텍처로 dart에 대해서는 중요하지 않으니 넘어가자. 이 세 플롯과 한 점의 색상은 각 모델들을 학습한 뒤 나온 성능을 나타낸다.
이 그림에서 x축이 학습률이고 y축은 규제 강도로 로그 단위를 따르고 있다. 이 걸로 알수 있는 점은 두 하이퍼 파라미터 사이의 상호 관계가 단순하지 않다는걸 알수 있다. 이 그림을 잘보면 강처럼 생긴 것의 중간에 보면 가장 좋은 학습률과 규제 강도를 찾을 수가 있겠다.
중간 질문) 하이퍼 파라미터를 찾는데 경사 하강법을 사용할 수 있을까?
하이퍼 파라미터를 찾는 건 아주 중요한 연구 분야 중 하나인데 이 강의의 범위를 넘어가지만 다양한 방법들이 있다. 예시를 들자면 파이토치로 파이썬 코드로 역전파를 간단하게 구현할수 있었듯이 최적화 방법를 사용하기 위해서 이너 루프와 아우터 루프를 구현하면 되는데,
여기서 이너 루프는 기존 모델의 학습 파라미터를 최적화 하는데 사용하여 그라디언트를 계산하고 초기 하이퍼 파라미터값에 따른 모델 성능을 구하고. 아우터 루프는 하이퍼 파라미터의 그라디언트를 학습하는데 사용하면 된다. 이런 방식으로 하이퍼파라미터를 탐색하는 다양한 논문들이 있기는 한데 (생략)

아무튼 페이스북이나 구글 등 수 많은 GPU 자원을 사용할수 있는 곳에서 일한다면 이런 하이퍼 파라미터 탐색 방법을 쓸수 있겠지만 그렇지 않은 경우 효율적인 하이퍼 파라미터 탐색 방법을 사용하여야 한다. 수 많은 하이퍼 파라미터를 탐색할 필요 없이 좋은 하이퍼 파라미터를 찾는게 가능하니 너무 걱정할 필요는 없다.

1. 초기 비용 확인하기
아무튼 사용 가능한 GPU 자원이 많지 않을때 우리가 할수 있는 방법으로 첫번째 단계는 우선 신경망 모델을 구현하고 초기 비용을 확인해보자. 비용 함수에 대해서 여러가지를 이미 살펴보았고, 교차 엔트로피 같은걸 사용한다고 하면 - log(클래스 개수)로 나타낼수가 있겠다.
모델을 구현한 뒤에는 가중치 감쇄를 사용하지 않고, 한번만 학습하여 초기 비용을 확인해보자. 한번만 학습 하다보니 계산량도 크지 않고 빠르게 구할수 있을건데, 비용이 잘못되어 있다면 버그가 있다고 볼수 있고 이 버그를 해결하면 되겠다.

2. 다양한 설정과 일부 데이터만 가지고 학습되는지 확인하기
다음 단계로 할 일은 훈련 데이터셋의 아주 작은 샘플을 가지고 오버피팅을 시켜보는것인데, 5 ~ 10개의 미니배치를 사용하면 된다. 이 소수의 데이터를 가지고, 규제를 하지 않은 채 100% 정확도를 얻을만큼 오버피팅을 시키면 되겠다.
이렇게 하면서 계층 수를 늘린다거나 학습률을 조정한다거나, 가중치 초기화 방법들을 조정해나가면서, 훈련 데이터가 적은 만큼 학습 시간도 작다보니 100 정확도에 도달하는 하이퍼 파라미터를 빠르게 찾을수가 있겠다. 만약 10개 정도의 배치 가지고 학습할수 없으면, 전체 데이터를 가지도 학습할수 없을거고 그렇지 않다면 문제가 없다고 볼수 있겠다.
아무튼 이 방법으로 다양한 경우들을 여러번 반복할 수 있을 것이고 모델 아키텍처에 알맞은 최적화 설정, 하이퍼 파라미터 설정에서 버그가 되는 것들을 잡아낼수 있다. 다만 이 단계에서는 최적화 과정을 아주 작은 훈련셋 가지고 디버그 하기 위함이지 규제나 검증셋으로 일반화를 하기위한게 아니니 이런것들을 고민할 필요는 없다.

3. 적절한 학습률 찾기
이번에는 이전 단계에서 구한 신경망 아키텍처와 훈련 데이터 전체를 사용해서 학습률을 찾아 보고 전체 학습 셋에서 비용을 빠르게 줄일수 있도록 해보겠다. 이전 단계를 통해서 우리가 구한 신경망 모델이 데이터를 잘 학습할수 있도록 설계되었는지 확인했다면, 이번 단계에서는 이전 단계에서 구한 하이퍼 파라미터를 그대로 가지고 오고, 학습률만 바꿔나가면되겠다.
여기서 목표는 100번 정도 훈련 셋으로 학습해 나가면서 비용을 크게 감소시키는 것인데, 적절하게 값들이 설정되었다면 초기 비용은 매우 크겠지만 백에서 수천회 학습하는 과정에서 지수적으로 비용이 감소하게 되며, 신경망 아키텍처를 다루는 문제에서 공통적으로 이런 경향을 보인다.
이 단계에서는 적절한 학습률을 찾기 위한 것이다 보니 한번 학습할때마다 수백에서 수천번 반복해도 되고, 여러 가지 경우를 반복하면서 첫 100회 반복때 가장 잘 수렴하는 학습률 값을 사용하면 된다.

4. 작은 간격으로 하이퍼 파라미터 탐색하기
다음으로 4번째 단계에서는 일정한 아주 작은 간격의 하이퍼 파라미터를 사용하여 학습률과 감쇄률/규제강도를 탐색하는 것으로 이전 3번째 찾은 값을 중심으로 보면 되겠다. 이전 단계에서 대략적인 하이퍼 파라미터를 잘 찾은 다음 이번에는 아주 작은 구간 간격으로 적합한 값을 찾다 보니 어떤 값을 사용하던 간에 크게 나쁜 모델이 만들어지지는 않는다.
전체 훈련 셋을 5~ 10 에폭 정도 학습 한 뒤에, 검증 셋으로 이 모델의 일반화 성능이 얼마나 좋은지 확인해보면 되겠다. 얼마나 작은 간격으로 하이퍼 파라미터들의 경우들을 다룰지는 여유가 되는데로 하고 결과가 어떤게 좋은지 비교해나가면 되겠다.

5. 하이퍼 파라미터 세부 조정, 더 길게 학습하기
4번째 단계 다음으로는, 이전 단계에서 구한 하이퍼 파라미터 값을 더 작은 간격, 세부적으로 조정하고, 더 길게 학습해보면 된다. 이 과정에서 한 에폭마다 몇 시간에서 몇일이 걸릴지는 학습할 모델이 얼마나 크냐에 따라 달린 문제가 되겠다.

6. 학습 커브 보기
다음으로는 학습 커브를 보고 하이퍼 파라미터를 어떻게 조정해 나갈지를 판단하면 된다.

이 학습 커브를 보면 좌측에 있는게 학습률 비용이고, 우측 그래프가 정확도를 나타내는데, 여기 나오는 훈련, 검증 정확도를 보고 모델이 올바르게 학습되는지 나쁘게 학습되는지 판단할수 있다.

이 그림은 다른 종류의 학습 커브인데, 앞에서는 평평하게 가다가 어느 시점에서 떨어지기 시작하는 형태인데, 이 경우 초기화를 잘못 시켰다고 볼 수 있다. 왜냐면 훈련 시작 당시에 제대로 학습되지 않기 때문인데, 어떻게 초기화를 시킬지 조정해서 다시 시도해보면 되겠다.

다른 문제 상황 예시로는 비용이 처음에는 잘 줄어들었다가 어느순간부터 평탄해지는 경우인데, 이 경우 학습률 감쇄를사용해야 한다. 이 경우는 학습률이 너무 높아서 시간이 지남에 따라 제대로 수렴하지 못해 평탄해지기 때문이며, 학습률 감쇄로 학습률을 낮추면 되겠다.

이번 경우는 반대로 학습률 감쇄를 너무 빨리 사용한 경우인데, 학습률 커브가 잘 내려가다가 감쇄하는 지점이후로 완전히 평평해져버린다. 이렇게 학습률 감쇄를 너무 빨리 한 경우에는 초기 학습률로 계속 진행하고 나서 감쇄해야 되겠다. 지금까지 본 내용들은 학습률 감쇄를 했을때 훈련 비용의 이동 평균이 어떻게 되는지를 보았고,
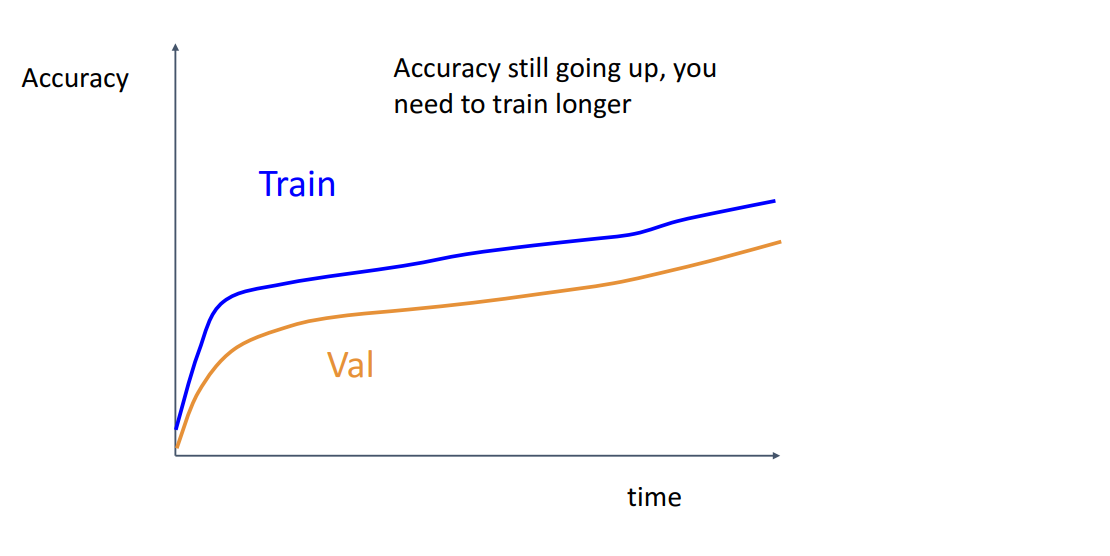
훈련, 검증에 대한 정확도 그래프로 곡선 형태에 따라 특성을 알수가 있다. 이 예시에는 시작 당시에는 지수적으로 증가하고 이후에는 천천히 선형적으로 증가하고 있는데 훈련과 검증 정확도 사이 어느정도 갭을 두고 계속 진행하는 경우에는 학습을 더 오래 해서 더 좋은 성능의 모델을 얻을수가 있다.

이번 예시는 오버피팅 특성을 보이는 그래프의 정확도를 보여주고 있는데, 훈련셋의 정확도는 시간이 갈수록 계속 증가하지만 검증셋의 성능은 고지점에 도달하고 나서 계속 감소하고 있으며, 훈련과 검증 정확도 사이 일정한 간격이 유지되지를 않는다. 이렇게 학습과 검증 정확도사이 간격이 증가하는 것은 오버피팅이 되고 있을을 나타내는 것이며, 이를 개선하기 위해서는 규제 강도를 높인다거나, 훈련 셋을 늘린다거나, 드문 방법으로 모델의 크기를 축소 시키는게 필요하다.

이번 그래프는 훈련과 검증 성능이 거의 동일하게 좋게 나오는 경우인데, 오버피팅이 존재하지 않으므로 좋다고 볼수는 있지만 훈련 셋과 검증셋의 성능이 같다는건 데이터를 과소 적합을 한다는 의미로, 좋지 않은 신호로 볼 수 있다. 이 경우 모델 크기를 늘리거나, 규제 강도를 낮춤으로서 성능을 더 개선할수가 있겠다.
(질의응답 생략)

이제 하이퍼 파라미터 탐색의 마지막 단계는 이런 비용 함수에 대한 곡선을 보고 어떻게 하이퍼 파라미터 구간을 설정해서 조정해나갈지를 판단해서 5번째 단계로 돌아가서 시간 여유가 있는 만큼 반복하면 되겠다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 3. 학습 후 할 수 있는 일 2(전이학습) (0) | 2021.03.09 |
|---|---|
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 3. 학습 후 할 수 있는 일 (0) | 2021.03.07 |
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 1. 학습률 스캐줄 learning rate schedule (0) | 2021.02.26 |
| 딥러닝비전 10. 신경망 학습하기 파트 1 - 4 규제 기법 (0) | 2021.02.26 |
| 딥러닝비전 10. 신경망 학습하기 파트 1 - 3. 가중치 초기화 2 (0) | 2021.02.25 |