퍼지 이론의 필요성
- 사람은 모호한 표현과 지식을 사용하나 컴퓨터는 정확한 수를 주어야하는 문제가 있음
- 인간의 모호한 표현을 처리하는 이론을 제공
퍼지 이론
- 1965년 로프티 자데가 소개.
- 모호하게 표현된 자료를 유용한 자료로 만들기 위해 퍼지집합, 퍼지논리, 퍼지수 개념과 계산방법이 개발
ex. 내일 비가 올 확률은 70% X , 내일 비가 올 가능성이 크다. O
퍼지 집합
- 사과 두어개를 사오라고 심부름 시키는 경우.
- "두어개" 2, 3개를 의미하나 2개가 더 강조됨.
- 퍼지 집합 : 원소 포함 여부가 참거짓이 아닌 포함 가능성으로 표현되는 집합
ex. "두어" = {(2, 1.0), (3, 0.5)}
"2 or 3" = {(2, 1.0), (3, 0.5)}
퍼지 집합과 소속 함수
- 퍼지 이론에선 불확실한 상황을 다룰때 숫자보다 자연여 구문 표현을 많이 사용.
ex. "철수는 젊다"
- 이 예시의 경우 "젊다"라는 구문 표현이 있지만 어느 정도인지 "젊다"를 정의해야함.
- 아래의 곡선은 퍼지 집합의 소속 함수(membership function)으로 각 나이 값이 퍼지 집합에 포함될 가능성을 의미.
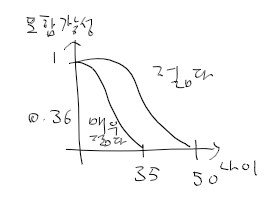
퍼지 집합의 정의
- 소속함수 mu_A(x) : 원소 x가 집합 A에 소속될 가능성을 나타내는 함수
-> 원소 x가 집합 A에 포함시 -> mu_A(x) = 1, 포함 안될시 -> mu_A(x) = 0
=> 이경우 고전 집합에서 소속함수 mu_A는 전체 집합 U의 모든 원소를 집합 {0, 1}에 대응, 한정한다.

- 소속 함수의 값이 0, 1사이 임의의 값을 가지는 경우 소속함수 mu_A는 각 원소를 집합 [0, 1]에 대응.

- 앞의 "두어개'에 대한 소속함수들은 좌측과 같고, 퍼지집합을 표현하면 우측과 같다.

- 고전 집합과 퍼지 집합의 비교
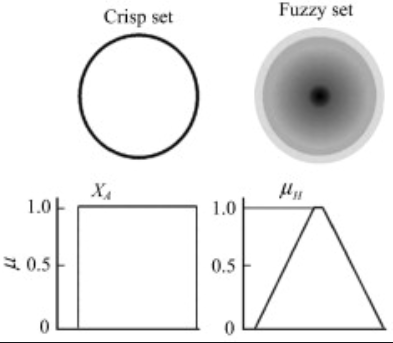
퍼지 연산
(생략)
퍼지 추론 현황
- 산업체 제어 프로세스, 시스템 모델링, 퍼지 지식 기반시스템 개발 등에 활용
1. 퍼지 규칙 조건부와 결론부는 언어적 변수 포함
2. 퍼지 규칙을 이용한 추론 절차는 일반적 규칙과 다름
언여적 변수를 사용한 퍼지 추론
- 1975년 자데 교수가 도입 -> 상업적 응용에 큰 역활
- 특정 변수를 수치 뿐만이 아니라 언어적 값도 사용가능하게 함.
ex. "키"는 보통 수치로 값을 사용. 언어적 변수를 사용시 "작다", "크다", "보통"이다. 값도 사용가능

탱크 수위 조절 제어 시스템에서의 예시
- "탱크 수위가 높으면 배수 밸브를 연다"라는 지식이 있다.
퍼지규칙 : IF 수위가 높으면 THEN 밸브를 연다.
- 3m가 높다고 가정시 다음과 같이 퍼지 집합으로 해석
HIGH = 0.1/2.0m + 0.1/2.2m + 0.3/2.3m + 0.3/2.4m +
0.5/2.5m + 0.7/2.6m + 0.7/2.7m + 0.9/2,8m +
0.9/2.9m + 1.0/3.0m + 1.0/3.1m + ...
- 밸브의 개방 정도도 퍼지 집합으로 표현 가능
1. 대략적 값을 정함
2. 현장 실무자 작업을 관찰하여 정함.
3. 시뮬레이션으로 양호한 결과를 내도록 함수값 조정
퍼지 추론
- 퍼지 규칙을 이용한 추론은 근사적이므로 근사 추론 approximate reasoning, 퍼지 추론 fuzzy reasoning이라고 함.
- 아래의 규칙이 존재하는 경우(긍정 논법)
IF x is A TEHN y is B
ex. 현재 수위가 "조금 높다"로 관측. "조금 높다"에 대한 소속함수가 정의됨. 규칙과 관측 결과가 주어질때, 추론 가능
규칙 : IF 수위가 높다 THEN 벨브를 연다.
사실 : 수위가 조금 높다.
추론 결과 : 벨브를 조금 연다.
* 이진 논리를 사용한다면 규칙 조건(수위 높다)과 사실(조금 높다)가 일치하지 않아 추론 불가
수위 조절 벨브 시스템에서 퍼지 추론
- 제시된 규칙과 사실

- 추론 과정이 더있으나 생략
'인공지능' 카테고리의 다른 글
| 인공지능 - 7. 게임 트리 (0) | 2020.11.11 |
|---|---|
| 인공지능 - 6. 탐색 과정 (0) | 2020.11.11 |
| 인공지능 - 4. 논리기반 지식표현 (0) | 2020.11.11 |
| 인공지능 - 3. 지식 (0) | 2020.11.11 |
| 인공지능 - 1. 개요 ~ 탐색 (0) | 2020.10.15 |