드디어 ORB 특징을 정리하게 되었다.
이전에 비주얼 슬램을 공부할떄 ORB 특징을 사용한다고 했는데
ORB 특징에 대해 이해하기가 힘들더라
다시한번보자
ORB Oriented Fast and Rotated BRIEF
OpenCV 연구자로서 가장 중요한 것중 하나로 ORB를 꼽을수 있겠습니다. 이 알고리즘은 Ethan Rublee이 ORB: SIFT나 SURF의 효율적 대안(ORB:An efficient alternative to SIFT or SURF) 이라는 논문에서 2011년에 소개되었습니다.
이 논문 내용은 SIFT나 SURF보다 비용 계산과 매칭 성능 측면에서 좋은 대안임을 보여주고 있습니다. 특히 SIFT와 SURF는 특허로 되어있어 비용을 지불해야되지만 ORB는 그런게 없슴다.
ORB는 기본적으로 FAST 키포인트 검출기와 BRIEF 기술자를 조합하여 성능을 개선한 변형물이라 할수 있겠습니다. 먼저 FAST로 키포인트를 찾아내고, 그다음 맨 위에 있는 N개의 점들을 찾기위해 해리스 코너를 사용하겠습니다. 여기서 멀티 스케일 피처를 만들도록 피라미드를 사용할수도 있겠습니다.
여기서 문제는 FAST는 방향을 계산하지 않는것인데 어떻게 회전 불변이 가능할까요? 저자는 여기서 변형을 해주었습니다.
ORB에서는 코너를 가진 패치 중심의 가중화된 강도를 계산하고, 이 코너점에서 중앙으로 향하는 벡터의 방향을 방위로 보고 있습니다. 회전 불변량을 개선하기 위해서, 반지름의 r인 원형 공간에 존재하는 x와 y에 대한 모멘트를 계산하겠습니다.
이제 기술자를 넘어와서보면 ORB는 BRIEF 기술자를 사용하고 있습니다. 하지만 BRIEF는 회전 변화에 좋지 않은 성능을 보이고 있어, 키포인트의 방향에 따라 브리프를 회전시켜줍니다.
위치 (x_i, y_i)에서 n개의 이진 특징 집합에 대해 테스트를 하기 위해 2 x n 형태의 행렬 S(이 픽셀들의 좌표)를 정의하겠습니다.
ORB는 각도를 2pi/30 (12개)로 이산화시키고, 미리 계산한 BIREF 패턴의 룩업 테이블을 만들어 줍니다. 키포인트 방향 theta가 일관될수록 올바른 점들의 집합 S_theta가 이 기술자를 계산하는데 사용되겠습니다.
BRIEF는 각 비트 특징들이 고분산과 평균이 0.5정도 되는 특성을 가지고 있습니다. 하지만 키포인트 방향으로 향하면 기존의 속성을 잃어버리고 더 분산됩니다. 여기서 고 분산인 경우 입력에 대해 다르게 반응하여 특징을 더 차별하게 만들어 버립니다.
다른 바람직한 특성은 각 테스트들은 결과에 영향을 주기 때문에 테스트의 상관관계를 해재하여야 합니다. 이를 위하여 ORB는 탐욕 탐색을 하여 모든 가능한 이진 시험을 수행하여 고분산과 평균이 0.5, 상관관계가 없는 값들을 찾으며 이를 rBRIEF라 합니다.
import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('./res/simple.jpg',0)
img2 = img
# Initiate STAR detector
orb = cv2.ORB_create()
# find the keypoints with ORB
kp = orb.detect(img,None)
# compute the descriptors with ORB
kp, des = orb.compute(img, kp)
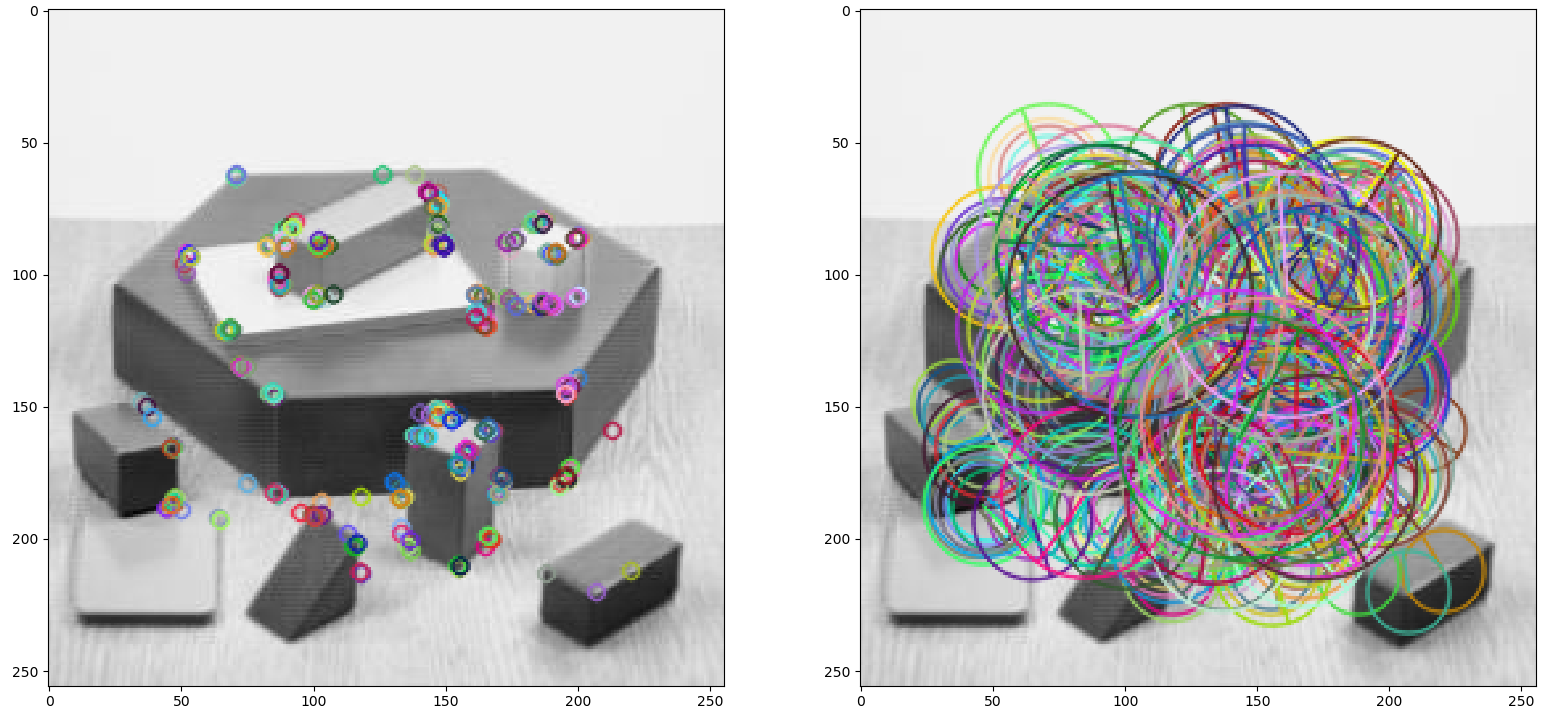
img = cv2.drawKeypoints(img,kp,img)
# draw only keypoints location,not size and orientation
img2 = cv2.drawKeypoints(img2,kp,img2, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
plt.subplot(121), plt.imshow(img)
plt.subplot(122), plt.imshow(img2)
plt.show()
'로봇 > 영상' 카테고리의 다른 글
| opencv-python 튜토리얼 - 27. 피처매칭 + 호모그래피 (0) | 2020.08.16 |
|---|---|
| opencv-python 튜토리얼 - 26. 피처 매칭 (0) | 2020.08.16 |
| opencv-python 튜토리얼 - 24. BRIEF (0) | 2020.08.16 |
| opencv-python 튜토리얼 - 23. FAST (0) | 2020.08.15 |
| opencv-python 튜토리얼 - 22. SURF (0) | 2020.08.15 |