14.3 경사 하강을 이용한 최대 우도 maximum likelihood as gradient descent
14.3.1 자세 공간 탐색 search in pose space
어떻게 식 14.9의 증분 우도 함수를 최대화 시킬지에 대한 질문을 살펴보겠습니다. 이것은 시간 t에서 모든 자세와 지도 공간에서 탐색을 수행합니다
하지만 지도 작성에서 고정된 루틴만 수행한다면, 모든 자세 공간에 대해 탐색하면 중분합니다. 이것은 지도의 공간이 매우 거대한 3차원의 자세 공간에서 계산량을 크게 줄여주는데, 이에 대해 살펴보기위해서 로봇의 자세가 주어진 상황을 생각해봅시다.
t번째 지도 $m^{(t)}$가 이전의 지도 $m^{(t-1)}$로부터 고정되고 결정론적인 루틴(점유 격자 지도 작성같은)으로 생성된다고 가정해봅시다. 여기서 최적화가 되어야할 파라미터는 자세로 다음과 같습니다.

여기서 $\bar{m}^{(t)}$($\bar{s}^{(t)}$, $o^{(t)}$, $m^{(m-1)}$)은 주장 자세 alleged pose $\bar{s}^{(t)}}$에서 지도 $m^{(t-1)}$에 관측 $o^{(t)}$를 증분적으로 반영하는것으로 구할수 있는 지도를 의미합니다. 여기서 자세를 알고있다고 고려하기 때문에 이 지도를 최근 센서 관측 $o^{t}$로 바꿀수 있으며 다음의 식을 얻을수 있습니다.

식 14.8 증분 신뢰도의 정의에 따라 다음과 같이 정리됩니다.

로그 우도 형태로 정리하면 다음과 같습니다.

정리하기 위해서 커지는 지도는 고정된 루틴으로 수행되며 전체 지도 공간을 탐색할 노력을 줄여줍니다. 이 결과 최대 우도 표현은 모든 자세 공간을 탐색하게 됩니다.
식 14.3의 결과는 이제 탐색을 수행하기 좋게 단순해졌는데, 특히 증분 사후확률을 최대화 하는 자세를 찾기 위해 시간 t에서 모든 자세 공간을 탐색하겠습니다. 연속 공간을 탐색하는 가장 일반적인 방법은 로그 우도 공간에서 경사 하강을 하는것이며, 다행이도 식 14.13의 모든 확률들은 미분가능합니다. 식 14.13의 우항에 있는 자세에 대한 로그 확률의 기울기는 다음과 같이 정리할 수 있습니다.

기울기는 추가되므로, 다음의 동작모델로부터 인지 확률의 기울기를 나눌수 있습니다.

경사 하강은 점차 내려가는 방향으로 추정치 $\bar{s}^{(t)}$를 바꾸고 이는 다음의 탐색 알고리즘에 적용할 수 있습니다.

여기서 k > 0는 경사 하강에서 필요한 단계의 크기로 0에 가깝습니다. 경사 하강의 시작점은 자세에 대한 간단한 동작(오도메트리 측정치)를 적용하여 구할수 있으며 다음과 같습니다.
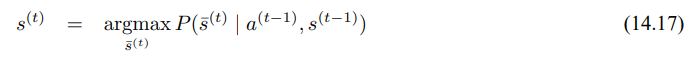
이는 5장에서 살펴본 노이즈 파라미터가 0으로 설정한 기구학적인 동작 모델을 이용하여 계산할수 있습니다. 경사 하강은 그러면 14.16의 갱신 법칙을 따라 반복하여 적용이 되고, 수렴 한계치를 만나게 됩니다.
14.3.2 기울기 계산
식 14.16에서 원하는 기울기를 계산하기 위하여 필요한 기술적인 세부사항들을 살펴보겠습니다. 인지 모델과 동작 모델에 대해 새부적으로 살펴보기 전에 미분 함수의 기울기 계산을 강조하는것이 중요합니다 로그 우도 함수의 기울기는 복잡할수 있으나 이들은 어느 동작 모델과 인지 모델을 미분하여 얻을수 있습니다. 이 모델은 미분할수 있으며 그래서 기울기는 이들 모두에서 계산될수 있습니다.
표 14.2는 로그 인지 모델의 일차 미분을 계산하는 알고리즘을 보여주고 있습니다.



표 14.2. 표 6.3의 거리계 모델을 이용한 로그 확률의 1차 미분 계산 알고리즘
기울기 계산은 직관적으로 수행될수 있는데 표 14.2에서 미분 계수 계산을 이해하기 쉽도록 정리하였습니다.


표 14.3 오도메트리 정보(표 5.5)를 이용한 동작 모델 p(s; | a, s)의 로그 일차 미분 계산 알고리즘
비슷하게 표 14.3은 오도메트리 기반 모델의 로그에 대한 일차 미분을 계산하는 알고리즘을 보여주고 있습니다.


표 14.4 분산이 b인 0평균 정규 분포의 1차미분 계산 알고리즘(표 5.2)
이 알고리즘은 0평균 노이즈 모델 prob()의 일차 미분이 필요하며 표 14.4에서 볼수 있습니다. 이 모델은 14.16에서 명확하게 요구되는것은 아니지만 중요합니다. 이는 미분의 연쇄법칙을 사용해서 복소수 함수의 미분을 계산하는 여러 방법들을 보여주고 있습니다. 빠른 경사 하강을 구현할때 여기있는 알고리즘들을 복수하는데신에 손으로 기울기를 계산해보시기를 추천합니다.
14.3.3 구현시 제안들 suggestion for the implementation
스캔 정렬에 대해서 이 알고리즘은 비대칭입니다. 이는 관측이 지도 m의 자유공간에 들어가기 때문인데, 지도가 점유된 지역을 보여주고 있는데 이 지역은 스캔 s에따라 자유로워야 합니다. 이 미스매치는 조정에 사용되지 않습니다. 이는 인지모델의 기본이 부족한것인데, 만약 이 모델의 대칭버전을 구현시에는 지도 m의 자유 공간에 들어가는 스캔 s 관측과 스캔 s의 자유공간이 들어가는 m의 지역 둘다 패널티를 주어야 합니다. 결과적인 인지 모델은 약간 더 복잡할수 있는데, 자세 s'에 대해 기울기를 계산하는것은 여기서 주어진 알고리즘에 아날로그적일수 있습니다.
더하자면 기울기 계싼은 특정 정보를 캐싱하여 속도를 크게 높일수 있습니다. 위에서 설명한대로 구현된다면 팬티엄 2 500MHz 프로세서를 사용할때 초당 10개의 기울기 계산이 수행되는것을 볼수 있겠습니다. 그리고 인지 모델과 일차 미분을 계산하는 과정은 더 오래 걸릴것입니다. 표 14.2의 기울기 알고리즘 9번째 줄에서 수행하는 가장 가까운 점유 공간 탐색또한 비용이 큰데, 추정 자세 $s^{(t)}$가 변할때 탐색은 또 반복되어야 합니다.
대안으로 x-y 공간의 그리드 공간에서 가장 가까운 위치의 일차 미분을 계산할수도 있습니다. 이 그리드 계산은 시작 시간이 다소 걸릴수는 있어도 테이불 룩업 작업을 사용하여 탐색시간을 줄여줍니다. 이 탑색의 결과는 근사화된것으로 가장 가까운 이웃을 찾아야 하는 지도의 모든 그리드셀 공간에서 수행되지는 않습니다. 이 기술을 사용하여 그리드 해상도가 10~20cm정도라면, 기울기의 결과가 우도 공간에서 언덕오르기로 잘 맞는것을 볼수있습니다. 게다가 기울기 계산은 2차수로 더 속도를 오릴수 있고 초당 수백회의 반복이 수행 될수 있습니다.
14.3.4 예제
그림 14.1은 스캔 정렬의 경사 하강을 사용한 두가지 예제 시퀀스를 보여주고 있습니다. 이 예제 둘다 표 14.2의 함수 일차 미분 로그 거리계 모델2를 사용하여 우도를 최대화 하였습니다. 두 예제들은 로봇이 이동하면서 기록되었고, 두번째 스캔은 첫번째에 상대적으로 축에 대해10cm, 30도 회전 에러를 가지게 추가하였습니다.
이러한 큰 에러에도 불구하고 루틴은 100회정도 반복하면 올바르게 정렬되었습니다. 그림 14.1은 초기 정렬과 10, 50, 100회 기울기 하강을 수행후 정렬결과를 보여주고 있습니다. 이 예지들은 우도 함수가 전역 최적화의 근접에 있어서 약간의 지역적 최소치들을 가지고 있음을 보여주고 있습니다. 현실에서 (3Hz) 시퀀스로 기록된 스캔을 사용하여 경사 하강 탐색 루틴은 실용적으로 항상 올바른 최대치로 수렴하고 높은 정확도로 이 스캔들을 정렬하였습니다.

표 14.1 스캔 정렬시 경사 하강을 이용한 예제. 두 경우다 초기 평행이동 에러가 각 축에대해 10cm씩, 회전 에러가 30도 정도로 존재합니다. 경사 하강 알고리즘은 최대 우도 정렬로 복원하였습니다.
14.3.5 한계 limitations
우도 최대화를 이용한 방법의 한계는 전역적인 최적 해를 구하는데 실패할수 있습니다. 이 문제는 단일 복도나 사이클이 존재하지 않은 환경을 지도 작성할때 이 문제는 발견할수 없는데, 여기에는 인접한 관측사이에 지역적 일관성만으로 역적으로 일관된 지도를 만드는데 충분하기 때문입니다. 하지만 사이클이 존재하는 공간에서 로봇은 이전에 모은 잠재적인 오도미터 에러가 포함된 데이터와 대응관계를 만들어야 하는데, 뒤의 자세 추정을 고쳐야만 합니다. 그 결과 증분 우도 함수 방법에서 지역 일관성은 전역 일관성을 만드는데 불충분하게 됩니다.

그림 14.2 가장 단순한 증분 최대 우도 방법을 사용하여 얻은 지도
- 지도는 지역적으로 일관적이지만 사이클이 닫힐때 이 방법은 실패하여 일관적이지 않은 지도로 만들게 됩니다. 단계별 우도 최대화의 한계를 보여주고 있으며, 사이클이 존재하는 환경에서 지도 작성의 어려움을 보여주고 있습니다.
그림 14.2는 이 예시를 사용한 문제를 보여주고 있습니다. 이 지도는 사이클이 존재하는 환경에서 얻은것을 보여주고 있습니다. 로봇은 여러 복도를 지나가 결국 초기 위치로 도달하게 됩니다. 지도를 따라가서보면 지역적으로 일관성을 가지고 있어 위치 추정의 에러가 발생하지 않습니다. 하지만 로봇이 사이클을 닫을때 누적된 위치 추정 에러가 지역적으로 수용하기에는 너무커지게 되어 이후 시간에서 지도를 고칠수 없게 되어 위 그림과 같은 영구적인 미스매치가 존재하게 됩니다. 이 결과 지도는 여전히 주행하는데 좋지만 더 큰 사이클은 더 큰 미스매치를 만들것이고 주행을 어렵게 할것입니다.
정리하자면 증분 최대 우도 방법은 다음의 주요 한계를 가지고 있습니다.
1. 이 방법은 큰 오도메트리 에러를 다룰수 없고
2. 이후 시간의 자세를 고칠수가 없습니다.
다음에는 이 두가지 결점을 다루기위한 확장된 개념들을 다룰것이고, 사이클이 존재하는 환경에서 더 신뢰성있는 동작을 수행하는 알고리즘을 구하겠습니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇 공학을 마치며 (0) | 2020.06.29 |
|---|---|
| 확률적 로봇공학 - 14. 빠른 증분 지도작성 알고리즘 (0) | 2020.06.28 |
| 확률적 로봇공학 - 12.3 SEIF SLAM 알고리즘 (0) | 2020.06.28 |
| 확률적 로봇공학 - 12.2 직관적인 설명 (0) | 2020.06.28 |
| 확률적 로봇공학 - 12. 희소 확장 정보 필터 (0) | 2020.06.28 |