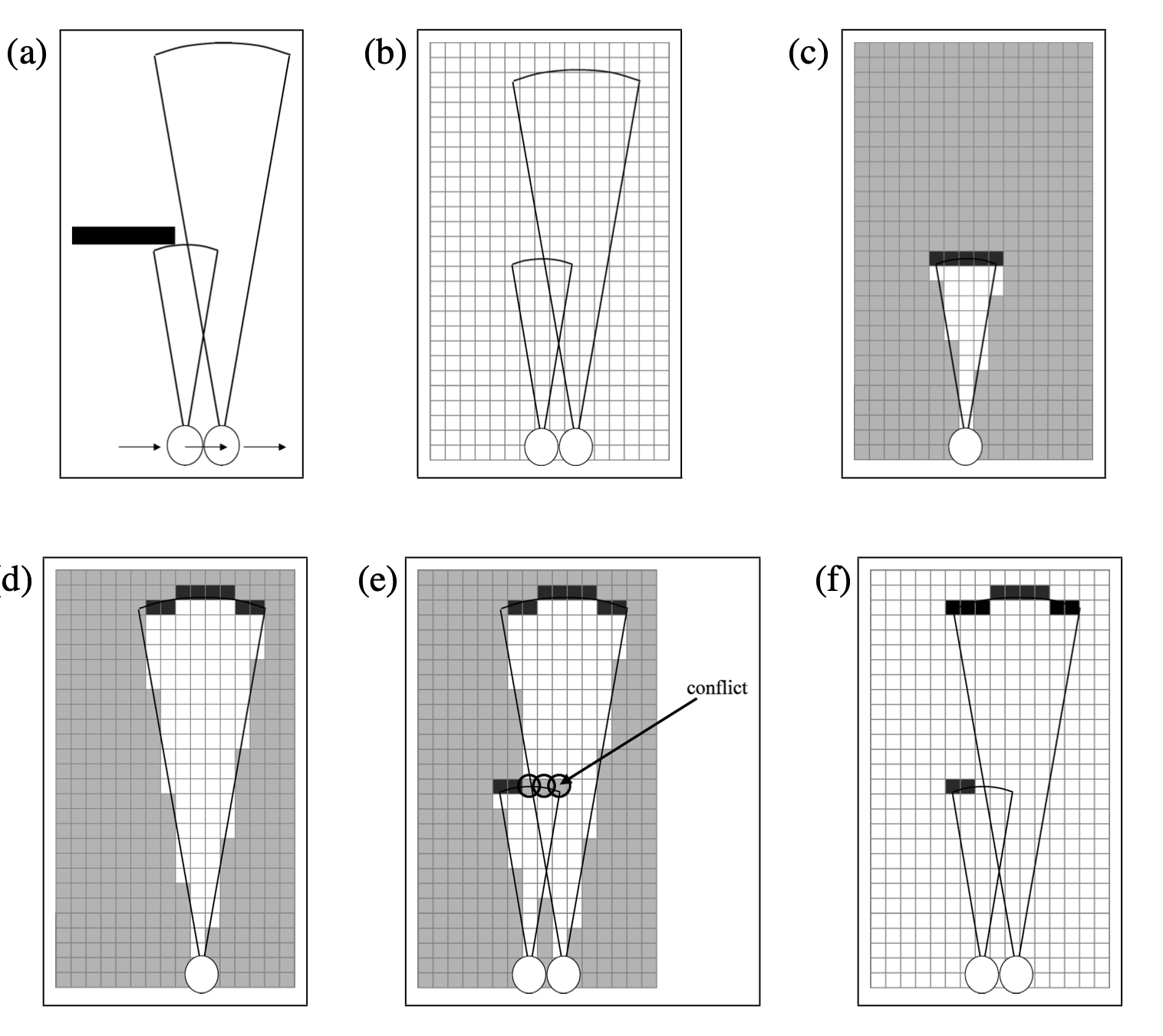
그림 9.7. 9.2장에서살펴본 표준 점유 격자 지도작성 알고리즘의 문제
(a) 와 같은 환경이 주어진다고 할때
(b) 로봇은 지나가면서 다음과 같은 관측치를 가지게 될것입니다.
(c), (d) 분해 방법으로 센서 빔을 각각의 그리드 셀과 각 빔에 대해 확률적인 지도로 맵핑한 경우를 보여주며
(e) 에서 두 결과의 합을 보여주고 있습니다. 하지만 원으로 표시한곳에 충돌이 발생하고 있습니다.
(f) 충돌이 일어나지 않는 경우의 지도.
9.4 점유격자 지도작성 사후확률 최대화 maximu a posterior occupancy mapping
9.4.1 의존관계를 유지사는 경우 the case for maintaining dependencies
이번에는 점유 격자 지도 작성 알고리즘의 기본 가정중 하나를 다시 볼건데 9.2에서 지도상 모든 다차원 공간에 대해 정의되는 지도 추론 문제를 단일 셀의 모음에 대한 지도 작성 문제로 분해하였습니다. 이 가정은 9.4에서 분해하여 사용되었는데, 이렇게 강하게 분해할 경우 알고리즘의 결과는 얼마나 신뢰할수 있을까라는 질문을 하게 됩니다.
그림 9.7은 이 분해의 결과로 생기는 문제를 보여주고 있습니다. 로봇은 벽과 만나는 두 소나 거리 측정치를 받는 상황을 보여주고 있습니다. 분해 방법으로 측정 거리에 존재하는 호 형태로 물체를 예측할 수 있기 때문에 이 호를 따라서 그리드 셀의 점유 값이 증가하게 됩니다. 그림 9.7c, d의 두 다른 측정치들을 합칠때, 그림 9.7e에서 충돌이 발생되는데, 표준 점유 격자 지도 작성 알고리즘은 이 충돌을 점유 값의 양과 음으로 합하여 이 충돌을 해결합니다. 하지만 이 결과는 신로할수 없는 두 측정치의 상대적인 프리퀀시를 반영하게 됩니다.
하지만 그림 9.7f와 같이 이런 충돌이 발생하지 않은채 센서 측정을 보여주는 지도가 존재하는데, 이는 센서 측정을 설명할수 있기 때문에 이 장애물을 존재하거나 안할수도 있는 곳으로 가정할수 있습니다. 다르게 보면, 원뿔형태의 측정에서 여러 그리드셀을 지울수 있는 사실은 이웃한 그리드셀사이 중요한 의존관계가 있음을 의미하기도 합니다. 지도 작성을 수ㅈ천개의 개별적인 그리드 셀 추정 문제로 분해시에는 이러한 의존관계를 고려해야하는 부분을 잃게 됩니다.
9.4.2 전방향 모델을 사용한 점유 격자 지도 작성
이 의존관계는 전체 사후호가률 대신 사후확률의 모드를 출력으로하는 알고리즘에 합칠수 있습니다. 이 모드를 지도 사후확률 로가리즘의 최대화 라고 정의할수 있는데 식 (9.1)에서 보았습니다.
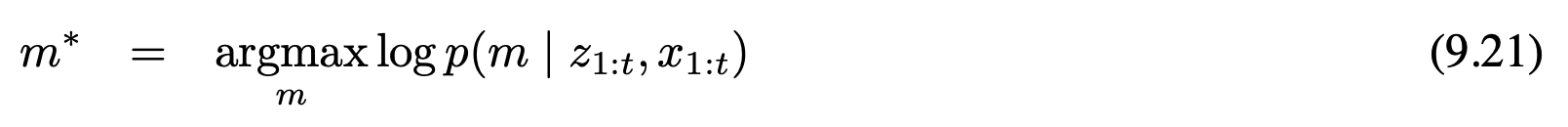
이 지도 사후확률은 지도 사전 확률과 관측 우도(식 9.11)로 나눌 수 있는데
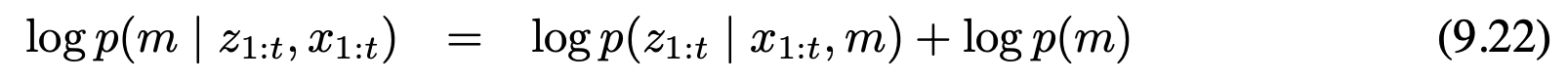
로그우도 log p($z_{1:t}$ | $x_{1:t}$, m)은 개별적인 관측 로그 우도 log p($z_t$ | $x_t$, m)의 합으로 나눌수 있습니다. 더 나아가 로그 사전확률 log p(m)은 아래 형태의 합이 되며 여기서 M은 그리드 세의 수 $l_0$은 식 9.7로부터 구할수 있습니다.
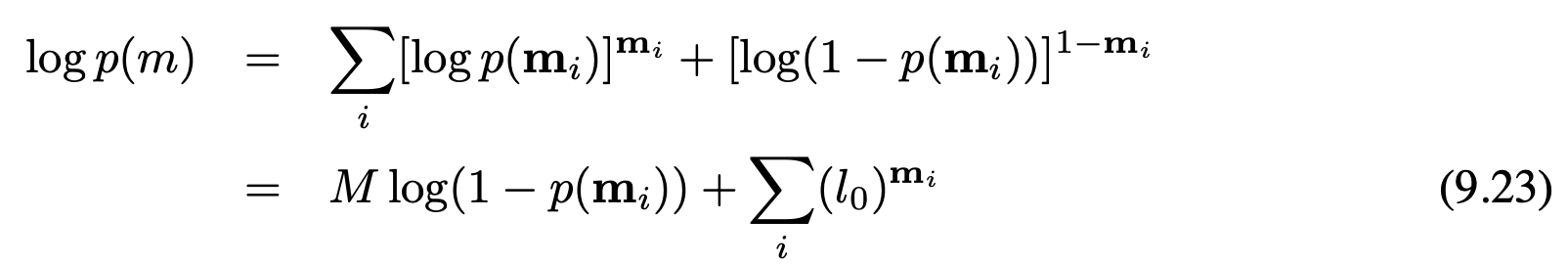
M log(1 - p($m_i$))항은 지도에 독립이라, 다음의 식과 로그 우도 데이터를 최적화를 수행할수 있습니다.
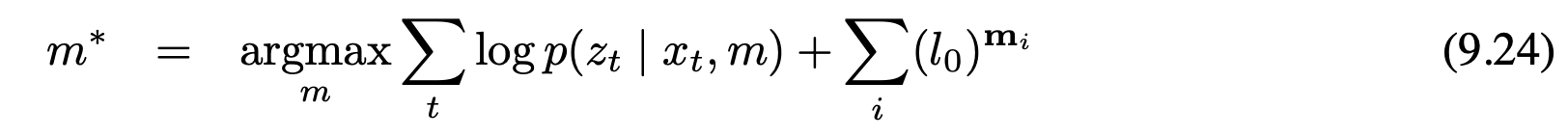

표 9.3 최대 사후확률 점유격자 알고리즘으로 역 모델 대신에 기존의 관측 모델이 사용되었습니다.
표 9.3은 이러한 로그 확률을 최대화 하는 언덕 오르기 hill climbing 알고리즘으로 2번째 줄에서) 자유 지도에서 시작합니다. 이 알고리즘은 4 ~ 6번째 줄에서 데이터의 로그 우도가 증가하면 그리드 셀의 점유 값을 뒤집습니다. 여기서는 점유 사전 확률 p($m_i$)이 1에 가까워서는 안되는데 이러면 전체가 점유된 지도로 될수 있기 때문입니다. 언덕 오르기 알고리즘으로 이 방법은 지역 최대를 찾게 되는데, 현실적으로 지역 최대치는 매우 적습니다.
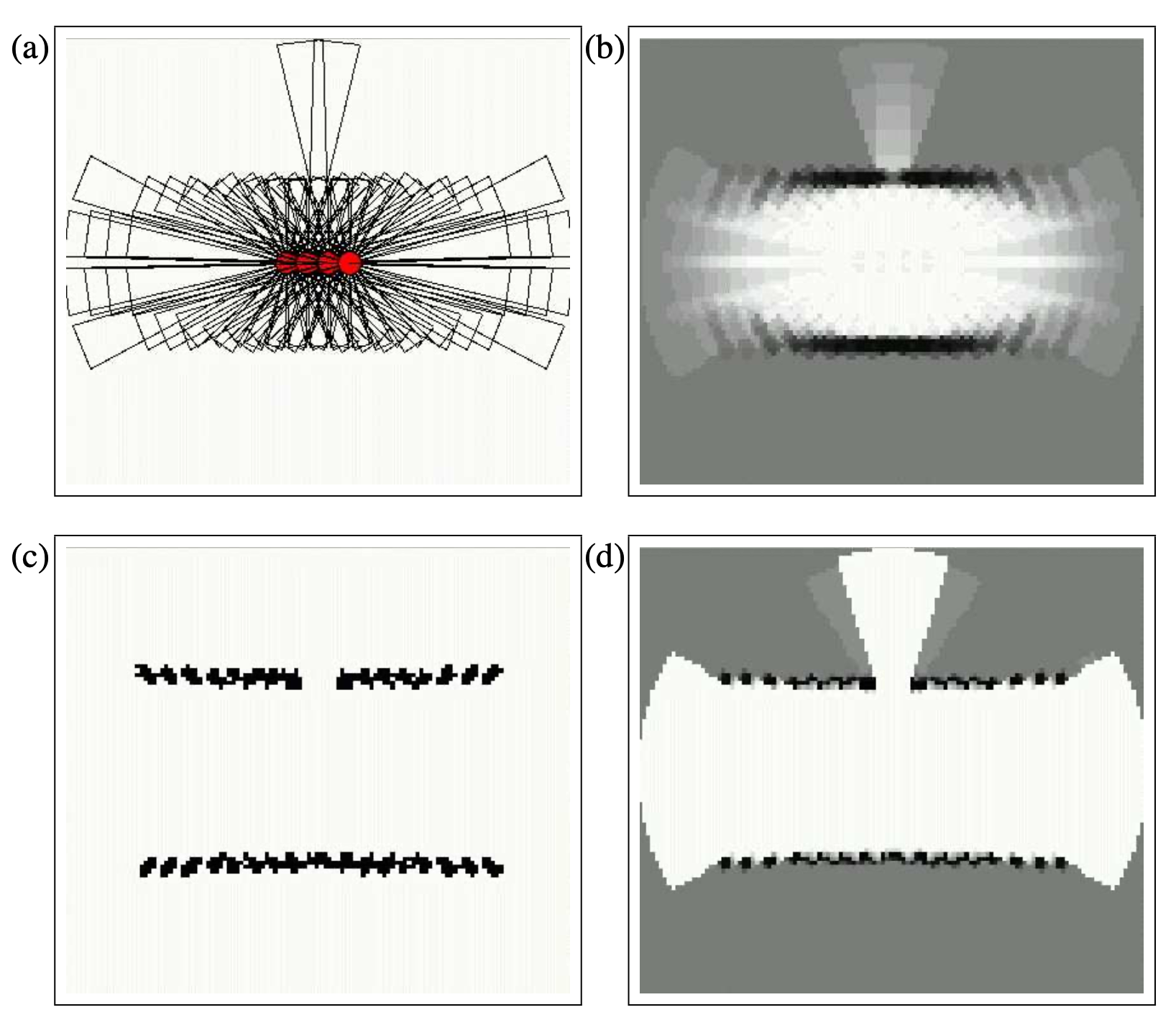
그림 9.8 (a) 노이즈가 없는 시뮬레이션으로부터 초음파 거리 측정치들
(b) 문이 열린 곳에서 표준 점유 지도작성기의 결과
(c) 최대 사후확률 지도
(d) 개별적인 그리드셀에 대해 지도 우도 함수의 민감도를 측정하면서 구한 지도상에 존재하는 불확실성들
그림 9.8은 MAP 점유 격자 알고리즘의 결과를 보여주고 있습니다. 그림 9.8a는 로봇이 문 열린 곳을 지나가면서 수집한 노이즈 프리 데이터집합을 보여주고 있습니다. 그림 9.8b에선 초음파 측정치의 일부가 문열림을 감지하는 반면에 일부는 문의 뒷면에서 반사되고 있습니다. 역모델을 사용한 표준 점유격자 지도작성 알고리즘은 문 열림을 획득하는대 실패했으며, 그림 9.8c에서 사후확률의 모드를 보여주고 있는데 이 모델은 문열림을 올바르게 찾았으며 표준 점유 격자 지도작성 알고리즘보다 더 적합한것을 알수 있습니다. 그림 9.8은 지도의 불확실성을 보여주고 있는데, 이 그림은 셀 단위 민감도 분석의 결과로 그리드 셀의 뒤집힘이 로그 우도를 감소시킴으로서 이 크기는 셀의 회색공간형태로 나오게 됩니다. 이 그림은 장애물뒤 그리드셀에 대해 최대 불확실성을 가지는 일반적인 점유 격자 지도와 비슷한데 여기서는 그림 9.8a와 같은 수직선이 존재하지 않습니다.
MAP 점유 격자 지도 작성 알고리즘은 수많은 제한들을 가지고 있으며 다양한 방법으로 개선될 수 있씁니다. 이 알고리즘은 최대 사후확률을 구하는 방법으로 남은 지도에 대한 불확실성을 반환하지 않습니다. 민감도 분석으로 이 불확실성을 근사시켰으나 이 근사치는 지역적인 모드만을 분석하기 때문에 과신된 것입니다. 더 나아가 이 알고리즘은 배치 알고리즘으로 증가적으로 수행될수가 없습니다. MAP 알고리즘은 모든 데이터를 메모리 상에 저장해야 하여 아무것도 없는 지도를 사용하는 대신에 기존의 점유 격자 지도 작성 알고리즘의 결과로 초기화 함으로서 계산상의 문제를 개선할 수 있습니다. 마지막으로 표 9.3의 5번째줄에서 그리드 셀 뒤집기에 의해 소수의 측정치가 영향을 받게 되는데, 각각의 합은 클지 몰라도 소수의 요소들은 최대치를 계산할때 확인됩니다.
9.5 정리
이번에는 점유 격자를 학습하는 알고리즘들을 살펴보았습니다. 여기서 다룬 모든 알고리즘들을 로봇의 위치 정보가 필요하여, 일반적인 지도 작성 문제를 해결할수는 없습니다.
- 표준 점유 지도 작성 알고리즘은 각 그리드 셀의 개별적인 점유 확률을 추정합니다. 이는 정적 환경에서의 2진 베이즈 필터 적응이라고 할수 있습니다.
- 다중 센서로부터 얻은 데이터는 단일 지도에서 2가지 방법으로 합칠수 있는데, 베이즈 필터를 이용하여 단일 맵을 유지시키거나 여러 지도를 각각의 센서 모델에 대해 유지시키고, 주행 결정시에 가장 신뢰성있는 점유값을 추출시키는 것입니다. 후자의 방법은 서로 다른 센서들이 다른 장애물타입에 따라 민감할때 선호되는 방법이기도 합니다.
- 표준 점유 격자 지도 작성 알고리즘은 역 측정 모델에 의존하는데 영항(관측)으로부터 원인(점유여부)를 구하기 때문입니다. 이는 이전에 살펴본 위치 추정에 있어서 베이즈 필터의 응용과는 다른데, 여기서 베이즈 필터는 원인으로부터 영향을 다루는 기존의 관측 모델을 기반으로 합니다.
- 기존의 관측 모델로 역 센서모델을 학습시키는것도 가능합니다. 이렇게 하기위해서 샘플들을 생성해야만하며, 함수근사기를 통해 역 모델을 학습하게 됩니다.
- 표준 점유 격자 지도작성 알고리즘은 각 점유 근사치에 대해 의존관계를 유지시키지 않는데 이는 지도의 사후확률 근사 문제를 수 많은 단일 셀 사후확률 근사 문제로 분해한 결과입니다.
- 전체 지도 사후확률은 일반적으로 그리드로 정의할수 있는 지도의 크기 때문에 계산할 수가 없습니다. 하지만 이는 최대화 될수 있는데, 사후확률 최대화는 지도가 항상 데이터에 대해 일관성을 갖도록 만들어 줍니다. 하지만 최대화를 위해서는 가능한 모든 데이턱 ㅏ필요하며 최대 사후확률 지도의 결과는 지도상에 남아있는 불확실성들을 반영할수가 없습니다.(그림 9.7f같은)
점유 격자 지도와 이 확장판들은 로봇 공학에서 많이 사용되고 있습니다. 이는 이 점유격자 지도를 얻기 쉬우며 로봇 주행에서 중요한 요소들을 구할수 있기 때문입니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇공학 - 10.2 확장 칼만 필터를 이용한 SLAM (0) | 2020.06.27 |
|---|---|
| 확률적 로봇공학 - 10. 동시적 위치 추정 및 지도 작성 SLAM (0) | 2020.06.27 |
| 확률적 로봇 공학 - 9.3.3 에러 함수 (0) | 2020.06.26 |
| 확률적 로봇공학 - 9.3 역관측 모델 학습 (0) | 2020.06.26 |
| 확률적 로봇공학 - 9.2 점유 격자 지도 작성 알고리즘 (0) | 2020.06.25 |