9.3 역관측모델 학습 learning inverse measurement models
9.3.1 관측 모델 뒤집기 inverting the measurement model
점유 격자 지도 작성 알고리즘은 주변 역관찰 모델 marginalized inverse measurement model p($m_i$ | x, z)을 필요로 합니다. 이 확률을 역이라고 부르는 이유는 관측치가 주어질때 지도 정보를 전달하기 때문입니다. 이는 i번째 셀에 대해 주변화 marginalized가 되는데, 전체에 대한 역모델의 경우는 p(m | x, z)가 됩니다. 이 기본 알고리즘을 확장하여 표 9.2에서 다뤄봤었습니다. 원칙적인 모델을 구하려면 일단 고전적인 측정 모델에서 시작하면 됩니다.
베이즈 정리로

여기서 p(m | x) = p(m)이라 하면, 로봇의 자세는 지도에 대해서 아무런 정보를 주지 않으므로, 더 쉽게 다룰수 있게 됩니다. 목표가 전체 지도에 대한 역 모델을 계산하는거라면 이제 끝났습니다. 하지만 구현할 점유 격자 지도작성 알고리즘은 각 그리드 셀 $m_i$의 주변부에 대한 사후확률을 근사시켜야 합니다. i번째 그리드 셀에 대한 역 모델은 i번째 그리드 셀의 주변을 선택하여 얻을수 있는데
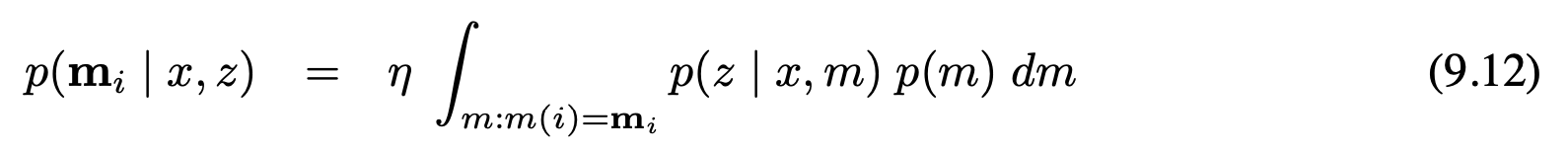
이 표현은 지도 전체에서 그리드 셀 i의 값과 같은 $m_i$들을 적분시키게 됩니다. 지도 전체 공간은 너무 크기 때문에 적분을 할수는 없는데, 이 표현을 근사화하는 방법에 대해 소개하겠습니다. 이 알고리즘에서는 측정 모델로부터 샘플을 만들고, 다항식, 로지스틱 회귀, 신경망 같은 함수 근사기를 사용해서 역모델을 근사시키게 됩니다.
9.3.2 전방향 모델로부터 샘플링 Sampling from the forward model
기본 아이디어는 단순합니다. 어느 그리드 셀 $m_i$에 대해 자세 $x_{t}^{[k]}$, 관측 $z_{t}^{[k]}$, 지도 점유 값 $m_{i}^{p[k]}$의 샘플을 생성한다면 입력을 자세 x, 측정 z로 하고 출력을 $m_i$에 대해 점유 확률로 하는 함수로 학습할수 있씁니다.
($x_{t}^{[k]}$, $z_{t}^{[k]}$, $m_{i}^{p[k]}$) 형태의 샘플을 다음 과정으로 구할수 있습니다.
1. 임의의 지도 $m^{[m]}$ ~ p(m)을 샘플해주세요. 예를들어 p(m)로 나타낼수 있는 지도 정보를 가지고 있다면, 정보로 임의의 지도를 그릴수 있습니다.
2. 지도 안에서 자세 $x_t^{[k]}$를 샘플해야합니다. 여기서 자세는 균일분포로 가정할수도 있습니다.
3. 관측 $z_{t}^{[k]}$ ~ p(z | $x_{t}^{[k]}$, $m^{[k]}$)를 샘플해주세요. 이 샘플 단계는 센서 측정치를 확률적으로 시뮬레이션하는 과정이 됩니다.
4. 지도 m에서 목표 그리드 셀에 대해 실제 점유 값 $m_i$를 추출해주세요.
이 결과는 샘플된 자세 $x_{t}^{[k]}$, 측정 $z_{t}^{[k]}$, 그리고 그리드 셀 $m_i$의 점유값이 됩니다. 샘플 단계를 반복하여 다음의 데이터 셋이 만들어 집니다.

이 트리플랫은 구하려는 조건부 확률 p($m_i$ | z, x)를 근사화 시키는데 사용할 함수 근사기의 예제들로 사용하겠습니다. 여기에 관측 z와 자세 x가 입력 값이고, 점유 값 occ($m_i$)가 함수 근사기 출력의 목표가 됩니다.
이 방법은 많은 속성들을 구하는데 실패할수도 있기 때문에 다소 비효율적일수도 있습니다.
- 센서의 인식 거리를 벗어난 관측치는 그리드셀에 대한 정보를 전달해서는 안됩니다. 이 관측은 2가지 의미를가지고 있는데, 첫째는 셀 $m_i$가 관측 범위 안에 있을때 트리플랫에 대한 샘플 생성 과정이 수행되는 점이고,두번째는 이 셀에 예측이 수행될때 측정치 z의 데이터 일부분만 함수 추정기의 입력으로 사용되기 때문입니다.
- 센서의 특성은 관측시에 로봇이나 그리드 셀의 절대 좌표에 시불변인데, 상대 좌표에서 문제가 발생합니다. 로봇의 자세를 (x y $\theta$$)^T$, 그리드셀 좌표 $m_i$ = ($x_{m_{i}}$ $y_{m_{i}}$$)^T$이면, 그리드 셀의 좌표는 아래의 변환을 통해 로봇의 지역 기준 좌표계 상으로 맵핑시킬수 있습니다.

원형 거리계를 가진 로봇에서는 그리드 셀의 자세를 극 좌표계(거리와 방위)를 사용해서 앤코드가 됩니다.
- 근처에 존재하는 그리드 셀들은 역 센서 모델을 이용해서 비슷하게 다루어져야 하는데, 각 그리드 셀에 별개의 함수로 학습하기 보다는 그리드 셀 좌표를 입력으로 사용하는 단일 함수로 학습시키는것이 효율적입니다.
- 만약 로봇이 기능적으로 동일한 센서로 처리를 한다면 역 센서 모델은 다른 센서들 사이에 같이 사용해도 됩니다. 원형 거리계를 장착한 로봇의 경우에 같은 역 센서 모델로 결과 센서 빔의 특성을 나타내게 됩니다.
이러한 불변성을 강화하기 위한 방법으로 적절한 입력변수로 함수 근사기를 만들면 되는데, 함수 근사기가 절대 좌표계에서 기반으로 하지 않도록 상대 자세 정보를 사용하는것이 좋습니다. 또 점유 예측과 관련없는 센서 관측치를 생략하고, 예측 과정을 센서의 인지거리 안에 있는 그리드 셀만으로 제한하는거이 좋은 방법이 될수 있씁니다. 이런 불변성을 개선하여 훈련 집합의 크기를 더욱 줄일수 있습니다.
'번역 > 구)확률적로봇공학' 카테고리의 다른 글
| 확률적 로봇공학 9.4 점유 격자 지도작성 사후확률 최대화 (0) | 2020.06.26 |
|---|---|
| 확률적 로봇 공학 - 9.3.3 에러 함수 (0) | 2020.06.26 |
| 확률적 로봇공학 - 9.2 점유 격자 지도 작성 알고리즘 (0) | 2020.06.25 |
| 확률적 로봇 공학 - 9. 점유 격자 지도 작성 (0) | 2020.06.25 |
| 확률적 로봇 공학 - 8.5~ 현실적인 고려사항들 (0) | 2020.06.25 |