
An Introduction to Statistical Learning with Application in R
3. 선형 회귀 Linear Regression
이번 장에서는 지도 학습 중 한 방법인 선형 회귀 Linear Regression에 대해서 배워보겠습니다. 선형 회귀는 양적 반응을 구하는데 유용한 도구라고 할수 있는데요. 오랫 동안 사용되기도 했고 수많은 책들의 주제로 다루어져 왔습니다. 이 방법이 이후 챕터에서 다룰 다른 현대적인 통계적 학습 기법과 비교해서 좀 지루할 수도 있겠지만, 이 방법은 여전히 유용하며 통개적 학습 기법에서 널리 사용되고 있습니다. 게다가 이 방법에 기반해서 더 나은 방법들이 나오고 있어요. 차후에 선형 회귀를 개선한 다른 통계적 학습 기법을 보게 되실겁니다.
결과적으로 더 복잡한 학습 방법을 배우기 전에 선형 회귀를 이해하는것은 매우 중요한 일이라고 볼수 있겠습니다. 이번 장에서는 선형 회귀 모델의 핵심 아이디어와 이 모델을 학습시키는데 사용되는 최소제곱법 least square에 대해서 배워봅시다.
한번 2장의 광고 데이터를 다시 떠올려봅시다. 그림 2.1에서는 TV, 라디오, 신문 매체의 광고 예산에 따른 특정 제품의 판매량을 보여주고 있었죠. 우리가 통계 분석가라고 생각해보고, 이 데이터를 이용하여 어떻게 내년에 광고를 하면 더 많은 제품을 판매할 수 있는지 생각해봅시다. 그러면 어떤 정보들이 판매량을 높이는데 도움이 될가요? 한번 이런 질문을 해봅시다.
1. 광고 예산과 판매량 사이에 어떤 관계가 있을까요?
우리의 첫번째 목표는 주어진 데이터, 광고 예산과 판매량 사이 상관관계가 존재하는지 알아내어야 합니다. 이 관계가 약하다면 광고할 필요는 없겟죠!
2. 광고 예산과 판매량 사이에는 얼마나 강한 관계가 있을가요?
광고 예산과 판매량 사이에 관계가 있다고 해봅시다. 그리고 여러분들은 이 관계가 강한지 알고싶다고 해요. 특정한 정도의 광고 예산이 주어질때 우리들은 판매량이 어떻게 될지 정확하게 예측 할수 있다면? 광고 예산과 판매량 사이에 강한 관계가 있다고 할 수 있을겁니다. 광고 지출에 따른 판매량 예측 값이 그냥 임의로 추정한 판매량과 큰 차이가 없다면? 이 경우에는 관계가 약하다고 불수 있겠습니다.
3, 판매량에 영향을 주는 매체는 어떤게 있을까요?
세 광고 매채, TV, 라디오, 신문이 판매량에 영향을 줄까요? 아니면 하나 혹은 두개의 매체만 영향을 미칠까요? 이 질문에 대한 대답을 구하기 위해선, 우리는 각 매체의 영향력을 나누어서 보아야 합니다.
4. 우리가 추정한 각 매체의 판매량에 대한 영향력이 얼마나 정확할까요?
특정 매체로 광고 비용이 증가할수록, 판매량이 얼마나 증가하게 될까요? 우리가 예측한 대로 판매량이 정확하게 증가되었나요?
5. 얼마나 정확하게 미래 판매량을 예측할수 있습니까?
특정한 정도의 TV, 라디오, 신문 광고 예산이 주어질때 판매량을 예측할수 있을까요? 그러면 그 예측이 얼마나 정확합니까
6. 매체와 판매량 사이 관계가 선형적인가요?
각 매채별 광고 지출과 판매량 사에 선형적인 관계가 있다면, 선형 회귀가 좋은 도구로 사용될 수 있습니다. 그렇지 않다면 선형 회귀를 사용 가능하도록 입력이나 출력의 현태를 변환 시킬 수도 있습니다. (* 저스틴 존슨 교수님의 컴퓨터 비전 5강 신경망에서 공간 변환을 통해 선형 분리를 하는 내용이 있었는데, 선형적 관계가 아닌 데이터를 변환을 통해 선형적인 관계로 구할수 있다는 의미로 보임)
7. 광고 매체 사이에 시너지 효과가 있었나요? 다른말로 하자면 서로 영향을 주는게 있었나요?
한번 탤래비전에 5만 달러, 라디오에 5만 달러를 쓴 결가 10만 달러 이상의 판매량을 얻었다고 합시다. 티비 광고만 5만 달러, 라디오 광고만 5만 달러치 한것 보다 더 큰 판매량을 얻을수 있었어요. 이 경우를 시너지 synergy 효과라고 할수 있으며, 통계학에서는 상호작용 interaction이라고 부릅니다.
3.1 단순 선형 회귀 Simple Linear Regression
단순 선형 회귀는 이름 그대로를 의미합니다. 입력 변수 X가 주어질때 양적인 반응 변수 Y를 추정하기 위한 매우 직관적인 방법이에요. X와 Y 사이에 선형적인 관계가 있다고 가정해봅시다. 그러면 수학적으로 이 선형적인 관계를 아래와 같이 정리 할 수 있어요.

여기서 $\approx$라는 표기는 우항을 좌항으로 근사시켰다? 좌항은 우항의 근사화된 모델? 우항과 좌항이 비슷하다? 정도의 의미를 가지고 있습니다. 위 (3.1)의 식을 X를 이용해서 Y를 회귀했다고 부르겠습니다. (regression Y on X, Y onto X) 예를 들어 X가 TV 광고 비용이고 Y를 판매량이라고 한다면, 학습된 모델을 통해서 TV 광고 비용으로 판매량을 회귀(양적 변수를 추측)할수 있겠죠.

식 3.1에서 $\beta_{0}$, $\beta_{1}$는 정해지지 않은 상수로, 선형 모델에서 절편(intercept, ex: y절편이라고 부르던 그거)과 기울기(slope)라고 부릅니다. 또 이들을 모델의 계수 coefficient 혹은 파라미터라고 부르기도 해요. 우리가 할 일은 주어진 훈련 데이터를 이용해서 모델의 계수인 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$ 추정치를 구하는 것이고, 이 추정된 계수 값으로 TV 광고 예산 값이 주어질때 이 식을 이용해서 예측 판매량을 계산할 수가 있겠습니다.
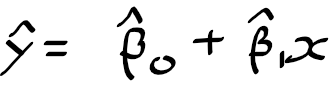
위 식에서 $\hat{y}$는 X= x가 주어질때, Y의 예측치를 의미해요. 여기서 x, y, z 같은 기호 위에 모자 hat ^을 씌워주는데, 이들은 알수 없는 파라미터, 계수를 추정하여 구한 값을 의미하고 있어요. $\hat_{y}$는 추정한 반응/ 출력 값이라고 할수 있구요.
3.1.1 계수들을 추정해보자 Estimating the Coefficients
현실에서는 $\beta_{0}$, $\beta_{1}$을 알수 없습니다. 그래서 예측 값을 구하려구 식 (3.1)을 쓰기 전에 반드시 주어진 데이터로 이 계수들을 추정해내야 해요. 한번 n개의 쌍으로된 관측치 observation pairs들이 있다고 해봅시다. 각 관측치들 obervations은 X의 측정값(measurement of X(과 Y의 측정값(measurement of Y)으로 이루어져 있어요.
* 관측치와 측정값을 정리하면, 관측치 observation는 (X, Y) 그러니까 X, Y의 쌍을 묶은 것으로하겠습니다.
* 측정값 measurement의 경우, 한 변수의 실제 값 $x_{1}$, $y_{1}$같은 변수들의 실제 값이라고 하겠습니다.
* 관측치와 측정 값의 차이는 관측치는 한번 관측을 했을때 얻은 X 측정값들, 혹은 X와 Y의 측정값들의 모음입니다.

다시 광고 예시로 돌아갑시다. 이 데이터는 n = 200(관측치가 200개), 200개의 시장에서의 TV 광고 예산과 그에 따른 제품 판매량으로 이루어져 있어요.(이 데이터들은 그림 2.1에 있는데 이 글 맨 위에 추가해두었습니다!) 우리들의 목표는 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$을 구하는 것이 되겠습니다. 식 (3.1)의 선형 모델이 주어진 데이터들을 학습해서 얻은 계수들이요. 그래서 아마 $y_{i}$ $\approx$ $\widehat{\beta}_{0}$ + $\widehat{\beta}_{1}$ $x_{i}$, i = 1, . . ., n의 형태로 정리할수 있겠죠.
정리하자면 우리는 200개의 데이터 점에 가능한 가장 가까운 close직선의 절편 $\widehat{\beta}_{0}$와 기울기 $\widehat{\beta}_{1}$를 찾는다고 생각하면 되겠습니다. 열마나 가까운지 측정하는 많은 방법들이 있는데, 그중에서 가장 많이 사용하는게 최소제곱법을 이용하여 오차제곱합이 최소화시키는 방법을 사용합니다. 이 방법을 이 장에서 사용해보고 다른 방법들은 6장에서 볼게요.

그러면 $\widehat{\y}_{i}$ = $\widehat{\beta}_{0}$ + $\widehat{\beta}_{1}$ $x_i$가 X의 i번째 값을 이용해서 Y의 값을 추정한다고 합시다. 그러면 $e_{i}$ = $y_{i}$ - $\widehat{\y}_{i}$ 는 i번째의 잔차(residual)를 의미하며, 여기서 잔차란 i번째 관측된 반응 변수(실제 Y)와 우리가 구한 모델로 예측한 i번째 반응 변수(예측 Y)의 차이를 말합니다. 그러면 잔차 제곱합(RSS; residual sum of squares)를 아래와 같이 정의 할 수 있어요.

그리고 이 식은 아래와 동등하다(equivalent)고 할 수 있습니다.

최소 제곱 방법은 RSS를 최소화 시키는 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$를 구하는 방법이에요. 여기서 미분을 사용하면, 이 RSS를 최소화 시키는 두 추정치는 아래와 같이 정리 할 수 있어요.

여기서 \bar{y} \equiv \frac{1}{n} \sum_{n}^{i=1} y_{i}이고, \bar{x} \equiv \frac{1}{n} \sum_{n}^{i=1} x_{i} 으로 샘플들(데이터들)의 평균을 의미합니다. 이를 정리하자면 (3.4)은 단순 선형 모델의 최소 제곱 계수 추정갑 least sqaure coefficient estimate 라고 부릅니다.
그림 3.1은 광고 데이터를 단순 회귀 모델로 적합/학습(fit) 시킨 것으로 , 그 결과 $\widehat{\beta}_{0}$ = 7.03, $\widehat{\beta}_{1}$ = 0.0475가 나오게 되었어요. 이 학습한 모델, 근사 식으로부터 TV 광고비가 1000달러를 씩 증가할 수록, 47.5 정도 제품 판매량이 증가한다는걸 보여주고 있습니다.
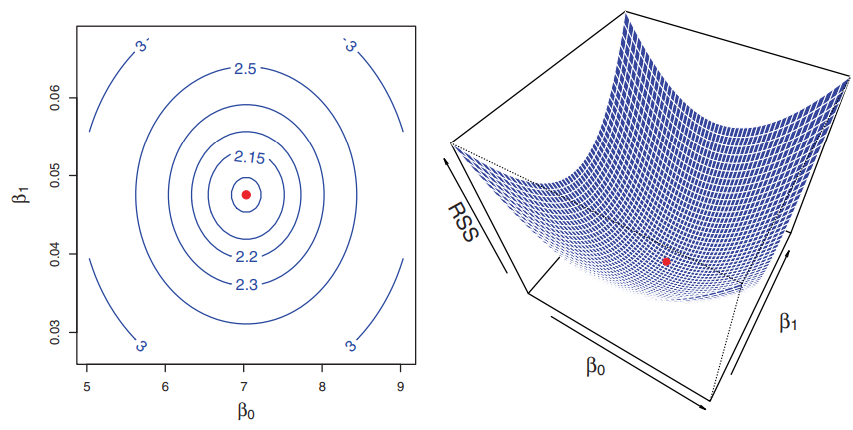
그림 3.2는 TV 광고비를 입력으로, 판매량을 출력으로 하는 광고 데이터를 사용하여 $\beta_{0}$, $\beta_{1}$의 값 변화에 따라 RSS가 어떻게 되는지 계산한 것을 보여주고 있어요. 두 그래프에서 빨간점은 RSS가 최소가 되는 지점으로 식 (3.4)로 구한 ($\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$)를 의미합니다.
3.1.2 계수 추정치가 얼마나 정확한지 평가해보자 Assessing the accuracy of the coefficient estimates
X와 Y의 실제 관계를 나타내는 식 (2.1) 생각해 봅시다. 이 식은 Y = f(x) + $\epsilon$이었는데, 여기서 f는 우리가 알지 못하는 실제 함수/모델이고, $\epsilon$은 평균이 0인 오차항이었습니다. 그럼 f를 선형 함수/모델로 추정을 했으면 이 식을 아래와 같이 고칠수가 있어요.

전에도 얘기했다시피 $\widehat{\beta}_{0}$은 절편 항, X = 0일때 Y의 기댓값/예측값이 되겠죠, 그리고 $\widehat{\beta}_{1}$는기울기로 X가 커질때 Y가 얼마나 증가하는지를 나타낼겁니다. 오차 항은 이 단순한 모델이 놓치는 모든 것을 나타내요. 실제 함수 모델에서, 실제 관계는 아마 선형이 아닐거고 Y에 변동을 일으키는 다른 영향력들, 혹은 변수같은게 있을거에요. 그게 오차 에러($\epsilon$)로 측정이되어 Y에 반영이 될수 있죠. 그래서 일반적으로 오차 항을 X에 독립이라고 가정하여 식을 새웁니다.
식 (3.5)의 모델을 population regression line 모집단 회귀선이라고 부르고, X와 Y의 실제 관계를 나타내는 최적의 선형 근사 식을 의미합니다. 식 (3.4)의 최소 제곱 회귀 계수 추정값들은 식 (3.2)의 최소 제곱 직선의 특성을 나타낸다고 할 수 있어요. 한번 그림 3.3의 우측 그래프를 보시면, 단순 시뮬레이션된 데이터들을 나타내는 두 개의 직선이 있는걸 볼 수 있어요. 임의로 100개의 샘플 데이터 X들을 생성시켰고, 아래의 모델에 입력하여 각 X에 대한 Y값들도 만들어 내었습니다.

요기서 $\epsilon$은 평균이 0인 정규분포로부터 생성된 오차항, 오차값이라구 할게요. 좌측 그림의 빨간선은 실제 관계 true relationship, 실제 모델인 f(X) = 2 + 3X를 보여주고 있습니다. 반면에 파란색 선은 관측된 데이터를 이용하여 최소제곱법으로 추정해서 구한 선이에요. 실제 함수, 모델, 관계는 보통 알려져 있지 않지만, 최소 제곱선은 식 (3.4)을 따라서 계수 추정치를 구하여 만들수는 있겠죠.

이를 정리하자면 실제 상황에서 우리는 관측치 데이터로 최소 제곱 직선을 구할수가 있어요. 하지만 모집단 회귀선은 관측할수는 없겠죠. 그림 3.3의 오른쪽 그림은 식 (3.6)에서 데이터 셋을 10번 샌성 시키고, 이 서로 다른 데이터셋으로 추정한 최소 제곱 직선을 그린것을 보여주고 있습니다. 같은 실제 모델로부터 생성되었지만 서로 다른 데이터셋이 만들어지다보니, 조금씩 다른 최소 제곱 직선들이 만들어 졌어요. 하지만 모집단 전체는 무수히 많고 관측할 수 없다보니 모집단 회귀선은 변하지 않아요.
얼핏 보기엔 모집단 회귀 직선과 최소 제곱 직선 사이 차이가 별로 없어 보이기는 한데, 데이터셋이 하나만 있다고 해 봅시다. 실제 모델의 직선과 데이터셋으로 추정한 직선이 있을것이고, 이 두 직선은 무엇을 의미하는 것일까요? 이 두 직선 중 추정하여 구한 모델은 샘플로 얻은 정보로 큰 모집단의 특성들(모집단 직선)을 추정하는 표준 통계적 방법을 보여준다고 할수 있을것 같습니다.
예를들어봅시다. 여러분들이 임의의 확률 변수 Y의 모평균 $\mu$를 알고싶다고 할때, $\mu$는 모르고, Y로 부터 n개의 관측치 $y_{1}$, . . ., $y_{n}$이 있다고 해 봅시다. 그러면 이걸로 모평균 $\mu$를 추정할 수 있겠죠. 그러면 가장 가능성이 큰 추정량은 $\hat{\mu}$ = $\bar{y}$이며, \bar{y} \equiv \frac{1}{n} \sum_{n}^{i=1} y_{i}는표본평균을의미합니다.
표본 평균 sample mean과 모 평균 population mean은 다릅니다, 하지만 일반적으로는 표본 평균이 모 평균을 잘 추정한 값으로 생각할 수 있습니다. 같은 방식으로 선형 회귀에서 알수 없는 계수인 $\beta_{0}$, $\beta_{1}$로 모평균 직선을 그릴수가 있지만, 이 계수는 알수 없으니 식 (3.4)로 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$를 추정하면 되고, 이 추정한 계수로 최소 제곱 직선을 정의할수 있겠습니다.
선형 회귀와 확률 변수의 평균을 이용한 추정 사이에 비슷한 건 이들이 편향 bias라는 개념을 기반으로 한다는 점입니다. $\mu$를 추정하기 위해서 $\hat{\mu}$를 한다고 해봅시다. 이 추정량이 편향되어있지 않다면(unbiased), $\mu$는 $\mu$와 동일하다고 볼 수 있습니다. 이게 뭘 의미하냐면, $y_{1}$, . . ., $y_{n}$로 구한 $\hat{\mu}$가 $\mu$보다 크게 추정될 수도 있고, 다른 관측치를 사용한 경우 표본 평균이 모 평균보다 낮게 추정될수도 있습니다. 하지만 아주 많은 관측치로 다양한 추정치들을 얻고, 이들을 평균을 낼수 있으면 모평균과 가까워 지겠죠. 그래서 불편향 추정량 unbiased estimator은 실제 파라미터를 과소, 혹은 과대 추정을 하지 않습니다.
불편성의 성질이 식 (3.4)로 구하는 최소 제곱 추정량에도 적용 되고 있습니다. 우리가 특정 데이터셋로 $\beta_{0}$과 $\beta_{1}$을 추정한다면, 아마 $\beta_{0}$가 $\beta_{1}$에 정확한 추정값을 구하지는 못할 겁니다. 하지만 크고 다양한 데이터셋으로부터 추정값들을 평균을 낸다면, 정확한 값을 구할 수 있겟죠. 그림 3.3의 오른쪽 그래프에서 수 많은 최소 제곱 직선의 평균으로, 서로 다른 데이터셋으로 추정해서 만든, 이 평균이 실제 모 회귀 직선에 아주 가까운 것을 확인하실 수 있겠습니다.
(*지금 보고 있는 내용들은 통계학에서 점추정 관련 내용으로 이전에 관련 내용을 부족하게나마 정리한 적 있음)
throwexception.tistory.com/957
임의의 확률 변수 Y의 모평균 $\mu$를 추정하는 문제를 계속 다뤄봅시다. 여기서 이런 질문을 할수 있겠죠? $\mu$를 추정한 $\hat{\mu}$가 얼마나 정확한가요? 우린 조금전에 아주 많은 데이터셋으로 $\hat{\mu}$를 구하고 이들의 평균이 $\mu$에 아주 가깝다는것을 봣엇습니다. 하지만 추정량 $\hat{\mu}$하나 만으로는 모 평균을 $\mu$ 과하거나 과소하게 추정할수 있을겁니다. 그러면 이 추정량 $\hat{\mu}$는 모평균과 얼마나 멀까요? 일반적으로 이 질문에 대한 대답은 $\mu$의 표준 오차 standard error로 구할 수 있습니다. SE($\hat{\mu}$)로 표기하며, 이 식은 아래와 같아요.

위 식에서 $\sigma$는 각 $y_{i}$들에 대한 표준 편차를 의미합니다. 편하게 말하면, 표준 오차 Standard Error는 실제 모평균 $\mu$과 추정량 $\hat{\mu}$가 평균적으로 다른 정도, 다른 크기를 알려준다고 할수 있어요.(표준 오차는 분산의 평균) 식 3.7은 표준 평차가 n에 따라서 얼마나 줄어드는지, 관측치가 많아 질수록, $\hat{\mu}$의 표준 오차가 작아지는것을 알수 있겠습니다.
비슷하게 $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$이 얼마나 실제 $\beta_{0}$와 $\beta_{1}$과 가까운지 궁금할수 있겠는데, $\widehat{\beta}_{0}$, $\widehat{\beta}_{1}$의 표준 오차는 아래의 식으로 구할수 있겠습니다. 여기서 $\simga^{2}$ = Var($\epsilon$)을 의미해요.

이 공식들이 유효해지려면 각 관측에 대한 오차 $\epsilon_{i}$는 공통 분산 common variance $\sigma^{2}$와 상관관계를 갖지 않는다고 가정하여야 합니다.(공통 분산은 잠시 검색 해봤는데, 인자 분석 관련 용어이긴하지만 이해하기는 힘들어 자세한 내용은 패스).

그림 3.1에서는 이 가정이 유효하지 않지만(오차도 상관관계에 영향을 주므로), 여전히 잘 추정하는것을 볼 수 있습니다. $x_{i}$가 크게 퍼지면 퍼질수록 표준 오차는 커져야 하겠지만 이 공식에서 SE($\widehat{\beta}_{1}$)는 작아지며,기울기를 추정하는데 더 큰 영향력을 주게 됩니다.
(제가 이해한 바로는 오차가 커질수록 기울기에 대한 표준 오차가 더 커져야 하지만, 위 식에서는 반대로 표준오차가 크게 줄어들어 정확한 기울기를 추정한다는 의미로 보임.)
$\bar{x}$가 0이라면($\widehat{\beta}_{0}$은 $\bar{y}$와 같아질 것임), $SE($\widehat{\beta}_{0}$)는 SE($\hat{\mu}$)와 같아지는 것을 볼수 있습니다. 일반 적으로, 공통 분산 $\sigma^{2}$는 알 수 없지만 주어진 데이터로 부터 추정은 할수 있어요 $\sigma$를 추정한 값을 잔차 표준 오차 residual standard error라고 부르는데, 이 RSE = $\sqrt{RSS/(n - 2}$로 구할 수가 있습니다.
표준 오차는 신뢰구간 confidence interval을 구하는데도 사용되요. 95% 신뢰구간은 실제 파라미터의 값이 95%의 확률로 속한다고 생각되는 값의 범위를 의미합니다. 이 범위는 샘플 데이터로 하한과 상항을 계산해서 구할수 있는데, 선형 회귀의 경우 $\beta_{1}$의 95% 신뢰구간은 아래의 형태를 가지며,

실제 값 $\beta_{1}$을 95%의 확률로 가질 신뢰 구간은 아래와 같습니다.

비슷하게 $\beta_{0}$의 신뢰 구간을 다음의 형태를 가지게 됩니다.

광고 데이터 예시를 보면 $\beta_{0}$의 95% 신뢰 구간은 [6.130, 7.935]이고, $\beta_{1}$의 95% 신뢰 구간은 [0.042, 0.053]이 된다고 할수 있어요. 그러므로 광고를 하지 않는 경우에 판매량이 6,130 ~ 7,940까지 떨어진다고 추정 할 수 있겠습니다. 하지만 텔레비전 광고 비용을 1000달러씩 증가시킨다면, TV 판매량이 평균적으로 42 ~ 53씩 증가하게 될겁니다.
표준 오차는 가설 검정 hypothesis test를 하는데도 사용되고 있어요. 가장 자주 사용하는 검정에서 귀무 가설로 null hypothesis로
$H_{0}$ : X와 Y 사이에는 상관관계가 없디.
대립가설 alternative hypothesis은
$H_{a}$ : X와 Y사이에 관계가 존재한다.
수학적으로 이 검정을 고친다면
$H_{0}$ : $\beta_{1}$ = 0 vs $H_{a}$ : $\beta$ $\neq$ 0
으로 고칠수 있겠습니다.
음.. 생각하다보니 가설 검정 부분은 다시 복습도 필요하고, 해야될 내용이 많다보니 여기서 생략하겠습니다.
3.1.3 모델 정확도 평가하기 Assessing the Accuracy of the Model
3.12의 귀무 가설을 기각한다면(대립 가설을 채택한다면), 그러니까 X와 Y 사이에 상관 관계가 존재한다면 이 모델이 얼마나 데이터를 잘 적합시키는지 정도를 정량화 하고 싶을 겁니다. 선형 회귀 모델의 적합 성능은 잔차 표준 오차 Residual Standard Error(RES)와 상관계수 $R^{2}$ 통계량으로 평가할 수 있습니다.

표 3.2에서는 (TV 광고와 판매량 데이터에 대한) 선형 회귀 모델의 RES와 $R^{2}$ 통계량, 그리고 F 통계량(3.2.2에서 설명함)을 보여주고 있어요.
잔차 표준 오차 Residual Standard Error
식 (3.5)의 모델로 돌아가서 생각해봅시다. 거기에는 오차항 $\epsilon$이 있엇죠. 그리고 이 오차항 때문에, 실제 회귀 직선을 알고 있어도, X가 있어도 완벽하게 정확한 Y를 구할수는 없었어요. RSE는 오차항 $\epsilon$의 표준편차 추정량이라고 할 수 있습니다.
실제 회귀 직선을 이용하여 구하는 평균 값이라고 할수 있는데, 아래의 식으로 계산 할 수 있어요.

식 3.1.1에서 RSS를 정의했었는데, 이를 다음의 식으로 줄수 있겠습니다.

광고 데이터 예시에서, 표 3.2를 보면 RSE가 3.26이었죠. 이는 실제 회귀 직선으로부터 각 마켓당 판매량의 차이가 평균적으로 3,260개 정도된다는 뜻이 됩니다. 다른 방법으로 생각해봅시다. 모델은 정확하고, 모델의 계수 $\beta_{0}$, $\beta_{1}$이 뭔지 안다고 해볼 게요. 그렇더라도 TV 광고 시 판매량 예측 치는 평균적으로 약 3,260개가 차이가 나게 될겁니다. 3,260개의 예측 오차가 받아들일만한지 아닌지는 이 문제의 상황에 따라 달라지겠죠. 이 광고 데이터셋의 경우 전체 시장에서의 판매량 평균은 14,000개 정도가 되니 오차 퍼센트가 3,260/14,000 = 23%나 됩니다.
RSE는 식 (3.5) 모델이 데이터에 잘 적합했는지 아닌지 적합 결함 정도를 측정하는데 사용할 수 있습니다. 이 모델로 구한 예측치가 실제 출력값과 매우 가깝다면 $\widehat{\y}_{i}$ $\approx$ $y_{i}$, i = 1, . . ., n 이라면 (3.15)는 아주 작아질것이고, 모델이 아주 잘 학습/적합했다고 할수 있겠습니다. 하지만 $\widehat{\y}_{i}$가 실제 $y_{i}$랑 멀다면, 그것도 여러 관측치에서 그러면 RSE는 큰 값이 나올것이고, 모델이 잘 학습했다고 할수 없을 거에요.
$R^{2}$ 통계량 $R^{2}$ Statistic
RSE는 모델이 적합 결함 정도의 절댓값을 알려주는데 absolute measure of lack of fit, 조금 고쳐서 적자면, 적합이 부족한 정도 알려준다. 하지만 항상 RSE가 좋은 건아니에요. $R^{2}$ 통계량도 잘 적합되었는징를 알려주는데, 비율의 형태로 설명할수 있는 분산의 정도 the proportaion of variacne explained를 알려주며, 0 ~ 1사이의 값을 가지고 Y의 스케일에 독립이라고 할수 있습니다.
$R^{2}$ 값은 아래의 식으로 계산할 수 있어요.

위 식에서 TSS = \sum ($y_{i}$ - $\bar{y}$ $)^2$으로 총 제곱합 Total sum of squares이고, RSS는 식 (3.16)에 정의하였습니다. TSS는 반응 변수 Y의 총 변동 Total Variance을 측정한 갑으로, 데이터들이 가지고 있는 변동성의 크기라고 할수 있어요. 반대로 RSS는 회귀를 한 후에 남은 설명 할 수 없는 변동의 크기를 의미합니다. 그래서 TSS - RSS는 (총 변동) - (설명 불가 변동) = (설명 가능 변동)으로, $R^{2}$는 입력 변수 X로 Y를 얼마나 설명할수 있는 비율을 측정하는 지표라고 할 수 있습니다. 여기서 설명력 amount of variability/explainability이란 회귀 모델가 실제 모델을 추정할수 있는 정도라고 할수 있을것같아요.
$R^{2}$ 통계량이 1에 가깝다면 회귀로 설명 할 수 있는 비율이 크다 -> 회귀 모델로 값을 잘 추정할 수 있다는 이야기이고, 반대로 0에 가깝다면 회귀 모델이 변동성을 잘 설명 할 수 없다 -> 값을 잘 추정하지 못한다고 할수 있겠습니다. 이런 경우는 선형 모델이 잘못 만들어지거나, 가지고 있는 오차가 너무 큰 경우에 생길수 있어요. 표 3.2에서 $R^{2}$는 0.61로 TV 광고비에 대한 선형 회귀 모델이 판매량에 대해서 2/3정도의 변동을 설명할수 있다고 할 수 있겠습니다.
식 (3.17)의 $R^{2}$ 통계량은 0 ~ 1사이 값으로 나타내다보니 식 (3.15)의 RSE보다 이해하기 쉽다는 장점이 있습니다. 하지만 무엇이 좋은 $R^{2}$인지 찾아내는건 쉽지 않은 일입니다. 사용하는 상황에 따라 달라질 수도 있거든요. 예를들어 물리학 문제에서 잔차가 작은 선형 회귀모델에서 데이터를 얻었다고 해봅시다. 이 경우에는 $R^{2}$ 값이 1에 아주 가깝겟지요. 하지만 $R_{2}$가 엄청 작다면 실험에 무슨 문제가 있다는걸로 볼수도 있어요,
식 (3.5)의 선형 모델은 데이터를 러프하게 근사시키는데 최고이지만, 측정되지 못한 인자/요소들 때문에 잔차 오차가 매우 커질수도 있습니다. 이 경우에는 변동의 아주 작은 일부분만 설명할수 있을 것이고 $R^{2}$는 0.1이하로 떨어 질수도 있어요.
$R^{2}$ 통계량은 X와 Y의 선형적인 관계를 측정하는 값으로 이를 상관계수 Correlation이라고도 부르며 아래와 같이 정의합니다.

$R^{2}$ 대신에 r = Cor(X, y)로 쓸수도 있고, 단순 선형 회귀 문제에서는 $R^{2}$ = $r^{2}$을 사용하기도 합니다. 정리하자면 상관 계수의 제곱은 $R^{2}$ 통계량과 동일하다고 볼수 있어요. 하지만 다음 섹션에서 다중 선형 회귀 문제를 다룰건데, 여기서는 여러 입력 변수들을 동시에 사용하여 반응 변수를 예측할겁니다. 상관계수는 수많은 변수들 사이의 연관성이 아니라 한 쌍의 변수끼리의 연관성을 다루기 때문에, 입력 변수와 반응 변수 사이의 상관관계라는 개념로 확장해서 다룰수는 어렵습니다. 차후 $R^{2}$가 어떻게 이 역활을 하는지 봅시다.
'번역 > 통계적학습법개론' 카테고리의 다른 글
| [통계기반학습개론] 3.4 마케팅 전략/3.5 KNN과 선형 회귀 모델 비교 (0) | 2021.02.06 |
|---|---|
| [통계기반학습개론] 3.2.2 & 3.3 회귀 모델에 대한 중요한 질문들과 다른 고려사항들 (0) | 2021.02.06 |
| [통계기반학습개론] 3.2 다중 선형 회귀 Multiple Linear Regression (0) | 2021.01.31 |
| [통계기반학습개론] 2.1.5 회귀 문제와 분류 문제 (0) | 2021.01.28 |
| [통계기반학습개론] 2. 통계적 학습 Statistical Learning (0) | 2021.01.28 |