Backpropagation applied to handwritten zip code recognition
1989년 Yann LeCun은 최초의 딥러닝 모델이라 할수 있는 LeNet을 소개하였는데, 이 논문에 대해 한번 리뷰해보자.
일단 초록의 내용을 정리하면
작업 범위에 제약을 주면 신경망의 학습 능력을 크게 높일수 있는데, 이 논문에서 그런 제약들이 어떻게 신경망 구조 전반에 역전파 과정으로 반영이 되는지 설명하려고 한다. 이 방법이 US 우편 서비스에서 제공하는 손글씨 우편번호 인식에 잘 적용되었으며, 신경망을 학습시킴으로서 정규화된 이미지를 분류할수 있게 되었다.
다시 정리하면 신경망은 작업을 어떻게 수행할지에 대한 제약 조건을 역전파를 통해 신경망에 반영을 반영 시킴으로서 학습 능력을 줄 수 있는데, 레쿤은 정규화된 문자 이미지를 입력으로 주었을때 분류 결과를 출력할 수 있는 신경망을 만들었다. 그 결과 미국 우편 시스템에서 손으로 적은 우편 번호를 잘 인식할 수 있었다고 한다.
이제 소개를 보면
레쿤은 1989년 단순 순자 이미지를 인식하는 연구를 했는데, 작업에 대한 사전 지식을 가진 신경망 모델을 설계해서 다른말로 신경망을 설계하고, 학습 시킴으로서 복잡한 경우에도 좋은 결과를 얻을수 있었다고 한다.
이 때 계산 성능이 저하되지 않을 정도로 신경망 파라미터를 줄이지 않는 것이 기본 원칙이며, 이를 지키면 올바르게 분류할 확률을 증가킬수 있었다.
이 논문에서는 Rumelhart가 1986년에 소개한 역전파 알고리즘을 미국 우편 번호 인식에 적용한 결과를 1989년 덴버가 했던 연구와는 다르게 특징 벡터이 아닌 이미지 자체를 바로 신경망에 넣음으로서 많은 양의 저차원 정보를 어떻게 역전파 신경망이 처리하는지 보여주고자 한다.
정리하면 1989년 레쿤은 특징이 아닌, 이미지 픽셀 같은 저 수준의 정보들을 역전파 신경망의 입력으로 사용하여 실제 우편 번호 인식에 적용하였다.
우편번호 데이터
레쿤이 사용한 우편 번호 데이터들은 손글씨 우편 번호들을 분할한 9298개의 디지털 이미지를 사용하였는데, 크기도 다양하고, 글씨체나, 도구도 다양했다. 이 중 7291개를 훈련용으로 사용하고 2007개를 성능 평가용으로 사용해지만 여기서 중요한 점은 훈련이나 테스트 데이터 셋 둘다 애매하거나 불류할수 없거나, 오분류된 예시들도 상당히 많이 있었다.
원래 우편 번호들은 40 x 60 정도의 크기로 다양했지만 선형 변환을 통해 16 x 16 크기의 이미지로 맞추었고, 스케일 조정이랑 중앙에 위치하도록 조정 시켰다.
데이터를 정리하면 총 9298개의 16 x 16 크기의 숫자 이미지를 사용

신경망 설계
신경망의 모든 층들이 완전 연결되어 있으며, 신경망의 입력은 16 x 16의 정규화된 이미지, 출력은 원핫 인코등 방식으로 10개의 데이터가 나오도록 되어있다.
특징 맵과 가중치 쉐어링
기존의 시각 인식 연구에서는 지역 특징을 추출하고, 그들을 조합하는것의 장점이 있었는데, 이 기법을 신경망 내부의 히든 유닛이 지역 정보들을 결합시킴으로서 쉽게 적용시킬수 있다.
물체의 특징은 입력 이미지의 다양한 위치에 나타날수 있으니 특징 검출을 하는게 좋지만 특징의 위치 정밀도는 크게 중요하지 않으므로 좀 잃어도 괜찬다. 1980년 푸쿠시마의 연구에 따르면 정확하지는 않더라도 대략적인 위치들은 다음 층에서 더 높고, 복잡한 특징들을 구하는데 필요하다고 한다.
입력의 어느 지점에서 특징여부를 구하는 방법으로 "가중치 공유" 기법을 사용할수 있겠는데, 1986년 rumelhart가 소개한 개념으로 여러 신경망의 연결들이 같은 가중치를 가지는것을 말한다. 가중치 공유는 파라미터 숫자를 줄일 뿐만이 아니라 기하 정보도 나타낼수 있는 장점이 있다. 이 연구에서의 첫 히든 레이어는 특징 지도라 부르는 여러 평면들로 이루어 져있는데, 한 평면의 모든 값들은 같은 가중치를 공유하고 있어 서로 다른 장소에서 같은 특징을 검출하게 된다.
위 내용을 정리하면 고전 패턴 인식 분야에서 저수준의 지역 특징을 조합하여 복잡한 특징을 구했다고 한다. 복잡한 특징을 구하는데 있어서는 정확하지는 않더라도 대략적인 위치만 있어도 되다는것 같다. 가중치 공유에 대한 내용은 아래의 그림으로 적었다.
신경망 구조
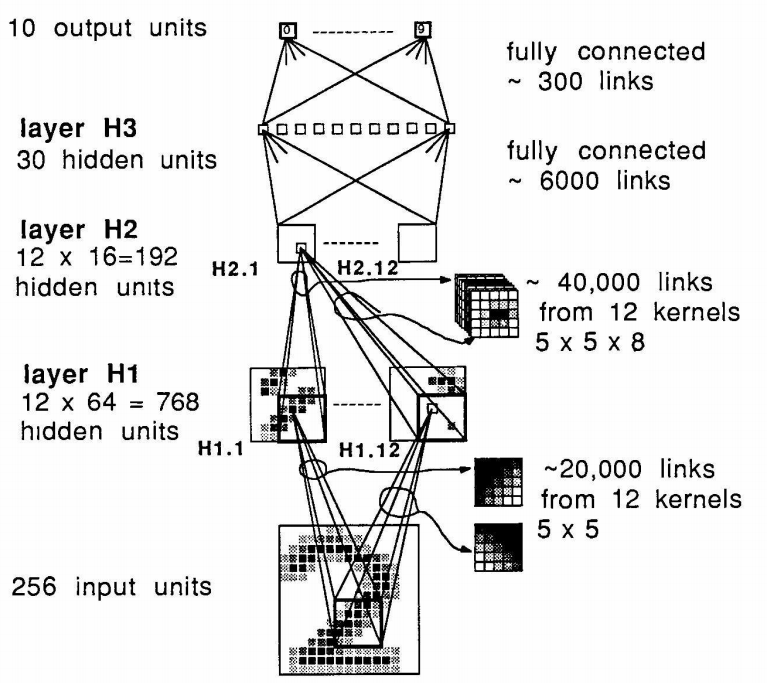
신경망은 H1, H2, H3이라 부르는 히든 레이어로 구성되어있으며, H1와 H2에 대한 연결이 강하게 제약되어있다. H1은 8 x 8 크기의 12개의 특징지도로 이루어져 있으며, 각 특징 지도를 H1 1, H1 2, H1 12의 식으로 부르겠다.
특징 지도의 각 값은 이미지 평면에서 5 x 5의 이웃들로 구하는데, H1에서 한 유닛당 입력 레이어에서 두 픽셀 간격으로 이동 시키면서 구하면, 입력 이미지는 언더 샘플링되고 일부 위치 정보가 사라진다. H1에서 H2에서도 이런 연산을 하여 특징 여부는 검출하지만 특징의 위치 정확도가 동일하지 않도록 하겠다.
커널을 스트라이드 2로 하여 슬라이딩을 시켜 16 x 16의 이미지가 8 x 8의 히든 레이어로 서브샘플링 시키고있다.

이미지의 어느 지점에서 중요한 특징의 경우 다른 위치에서 중요할수 있다. 그러므로 특징 지도가 주어질 때, 그 특징에 해당하는 유닛들의 경우 같은 가중치를 가지게 된다. 다시 말하면 H1 1의 64개의 유닛들은 25개의 동일한 가중치 셋으로 구한것이라 할수 있겠다. 이미지의 해당 부분에서 동일한 연산을 하여 구한것이며, 특징 지도를 이용한 이 함수, 연산을 5 x 5 커널을 이용한 비선형 서브샘플된 컨볼루션이라 생각할수 있겠다.
위 내용을 정리하면 하나의 커널로 컨볼루션 연산을 수행하여 하나의 히든 레이어를 구하므로 가중치 공유라고 부르며, 해당 커널이 가장 잘 나타내는 특징들 위주로 컨볼루션 연산 결과가 나오게 된다. 아래의 커널이 주어질때 "/"부분이 가장 잘 찾아지며, 텅빈 공간의 경우 컨볼루션을 하여도 아무것도 찾아지지않는다.

다른 특징 맵(히든 레이어)의 유닛은 다른 25개의 가중치(커널)으로 구하며, 특징 맵 끼리는 편향 또한 구하지 않으며 각 특징맵의 유닛은 컨볼루션 연산 후 편향을 더하여 구한다. H1 레이어는 768개의 유닛( 8 x 8 x 12)과 19,968개의 연결(768 x 25 + 268 x 1[편향])으로 이루어지며, 학습 가능한 파라미터는 1068개(768 히든 레이어+ 25 커널x 12커널 개수)뿐이다. H2 레이어도 12개의 특징 지도로 이루어져, 각 특징 지도는 4 x 4 크기의 평면으로 16개의 유닛을 가지며, 입력과 H1과 동일한 방식으로 연결되어 있다.
H2의 유닛들은 H1 특징 지도들로부터 얻은 지역적인 정보들을 가지고 있으며 5 x 5 크기의 8개의 맵(커널)로 구한다. 그래서 H2의 한 유닛의 입력은 200(5 x 5 x 8)개의 가중치와 평향들로 이루어진다. 정리하면 H2 레이어는 192개의 유닛(12 x 4 x 4)를 가지고 있고, 총 연결은 192 x 201(가중치 200+ 편향 1) = 38,592개의 연결들로 이루어 진다. 여기서 학습 파라미터 갯수는 2592개로 200개의 가중치 x 12개의 특징 지도 + 192개의 편향이 된다.
이제 대강 이 논문 전반에 대해 본것 같으니 마치자면
LeCun은 컨볼루션 연산을 이용하여 우편 번호를 인식 가능한 신경망 모델을 만들었다.
여기서 컨볼루션에 사용하는 각 마스크들은 원본 픽셀 이미지로부터 지역 특징들을 학습(역전파 알고리즘을통해)시켜 구하고, 이 마스크들은 주어진 이미지에서 중요하다고 하는 특징들을 검출하여 은닉 층들을 만들었다. 이 은닉층에 마스크로 컨볼루션을 더 함으로서 지역적이던 특징들이 혼합되도록 하였고, 그 결과 10개의 카테고리로 줄임으로서 입력 이미지로 부터 숫자 데이터를 구할수 있게 되었다고 할수 있을 것 같다.
ref
[1] en.wikipedia.org/wiki/LeNet
[2] Backpropagation applied to handwritten zip code recognition, 1989
[3] www.hellot.net/new_hellot/magazine/magazine_read.html?code=202&idx=42061&public_date=2018-08
'그외 > 논문' 카테고리의 다른 글
| Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning (0) | 2021.04.12 |
|---|---|
| StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks (0) | 2021.04.05 |
| 물체 인식을 위한 선택적 탐색 (0) | 2020.11.19 |
| 중, 고 레벨 특징 학습을 위한 적응적 디컨볼루션 신경망 (0) | 2020.11.18 |
| 합성곱 신경망의 시각화와 이해 (0) | 2020.11.17 |