저스틴 존슨 교수님의 강의만 들어서는 내용을 잘 알아들을수도 없고 이해가 잘 되지 않는 부분이 많아
학습 머테리얼들을 참고해서 적는다.
aikorea.org/cs231n/linear-classify/
Softmax 분류기
- SVM이 가장 흔하게 사용되는 분류기 2가지 중 하나로 살펴보았습니다 .다른 하나는 소프트맥스 분류기인데 다른 형태의 비용 함수를 가지고 있습니다. 아마 여러분들이 로지스틱 회귀 분류기를 전에 들어보았다면, 소프트맥스 분류기는 다중 클래스의 경우로 그걸 일반화 시킨것이라 할수 있겠습니다.
SVM이 아래의 출력을 각 클래스의 스코어, 점수로 보고있다면

소프트 맥스 분류기의 경우 더 직관적인 출력(정규화된 클래스별 확률)을 보여주어 확률적으로 이해할수 있겠습니다. 소프트 맥스 분류기에서 또한 아래와 같은 함수 형태, 맵핑 관계 자체는 바뀌지는 않으나
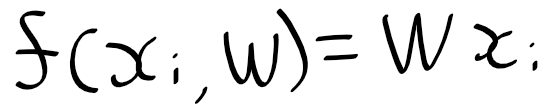
이 점수들을 각 클래스별 정규화 되지 않은 로그 확률로 볼것이며, 이 힌지 로스를 아래와 같은 교차 엔트로피 오차로 바꾸어 사용하겠습니다.

위 형태의 교차 엔트로피 오차에서 f_j는 클래스 점수 백터 f의 j번째 요소를 의미하고 있습니다. 이전에 데이터셋의 총 손실 full loss가 모든 훈련 데이터에 대한 손실의 평균으로 구하였었습니다. 여기서 함수 f_j는 소프트 맥스 함수로 아래의 형태를 가지고 있습니다.

소프트 맥스 함수는 실제 점수들을 입력받아 나누어 0에서 1사이의 값(확률)으로 만들어주는 함수라고 할수 있습니다. 총 교차 엔트로피 손실은 소프트 맥스 함수를 포함하고 있어 겉보기에는 복잡해보지만 쉽게 이해할수 있겠습니다.
정보 이론적 관점
실제 확률 분포 p와 추정 확률 분포 사이 교차 엔트로피는 아래와 같이 정리할 수 있습니다.

소프트맥스 분류기는 추정한 클래스별 확률들과 실제 확률 분포의 교차 엔트로피를 최소화 시키는 것이고, 여기서 실제 확률 분포는 모든 가능한 경우들 중에서 올바른 클래스를 나타내는 확률 분포를 말하는데 p =[0, . . ., 1, . . ., 0] (y_i 번째 자리에만 1이 있음. 원핫 인코딩의 형태)의 형태라고 할 수 있겠습니다.

그러므로 교차 엔트로피는 엔트로피와 쿨백-리블러 발산을 이용하여 아래와 같이 정리할수 있고,

델타 함수의 엔트로피가 0인 경우, 이는 두 분포 사이의 KL 발산 그러니까 예측 확률 분포와 실제 확률 분포사이의 거리(오차)를 최소화시켰다고 할수 있겠습니다. 다시 정리하자면 교차 엔트로피를 사용하는 목적은 올바른 대답에 속하는 모든 질량을 갖는 예측 확률 분포를 구하는 것이라 할수습니다.
엔트로피, 쿨백리블러 발산, 교차 엔트로피
- 엔트로피 : 정보의 불순도, 무질서의 정도
- 쿨백 리블러 발산 : Kullback-Leibler Divergence : 두 확률 분포 사이의 거리, 차이를 구하는데 사용
- 교차 엔트로피 : 두 확률 분포 사이의 거리
- 참조 링크 : ramees.tistory.com/64

SVM 대 소프트맥스
이 그림으로 소프트맥스 분류기와 SVM 분류기의 차이를 아라봅시다.

이 그림은 한 데이터가 주어졌을때 SVM과 소프트맥스 분류기의 차이를 보여주고 있습니다.
계산 결과 같은 스코어 벡터 f(행렬 곱으로 얻은)가 나오고 있는데, 차이점은 점수 f를 어떻게 해석하느냐, 이용하느냐에 차이가 있다고 볼수 있겠습니다.
SVM은 이 점수를 클래스별 점수로 해석하고, 비용함수가 올바른 클래스(2번 클래스, 파란색)이 다른 클래스보다 더 높은 점수를 받을 수 있도록 마진을 사용하고 있습니다.(올바른 클래스의 점수가 클 수록 비용이 줄어들 기 때문)
소프트맥스 분류기의 경우 점수를 각 클래스에 대해 정규화되지 않은 로그 확률로 보고 있으며, 이를 정규화를 시키고 올바른 클래스의 로그 확률이 더 높아지도록 만듭니다.(아닌 경우는 낮아지도록)

이 예시에서 최종 손실은 SVM의 경우 1.58, 소프트맥스 분류기의 경우 1.04지만 이 수치끼리는 비교해선 안되고 동일한 분류기와 동일한 데이터에 대해서 계산된 비용 끼리 비교할때만 의미가 있다고 할수 있습니다. 그러니까 가중치를 바꿔가면서 비용 함수로 구한 비용이 줄어드는지 전후 비교하는 것에 사용해야합니다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 5. 신경망 2 - 신경망 근사화와 컨벡스 함수 (0) | 2021.01.29 |
|---|---|
| 딥러닝비전-5. 신경망 (0) | 2021.01.25 |
| 딥러닝비전-4. 최적화 (0) | 2021.01.20 |
| 딥러닝비전-3. 선형 분류기 (0) | 2021.01.11 |
| 딥러닝비전-2. 이미지 분류 (0) | 2021.01.04 |