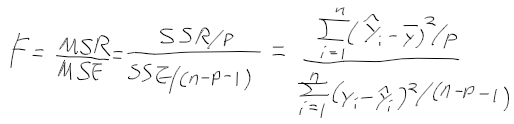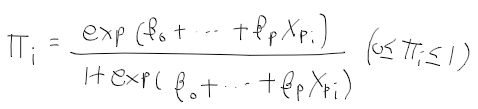선형 회귀 모형
- 입력이 주어질때 결과를 예측하는 모형
- i번쨰 목표 변수의 값을 Y_i, 입력 변수들의 값 X_1i, ... X_pi라 할때 아래와 같이 정의
- 입력 변수와 회귀 계수의 선형 결합의 형태로 된 모델
- beta_0, ..., beta_p는 회귀 모수 regression parameter or regression coefficient로 아직모르는상수
- eta_i는 Y_i의 근사오차. 오차는 서로 독립이고 평균이 0, 일정한 분산을 가짐
회귀 계수를 추정하기
- 최소제곱법 least sequare method을 사용
- 각 관측치와 회귀 선까지 거리(오차) 제곱의 합을 최소화하는 계수들을 구함.
- 각 회귀 계수 beta_i에 대해 편미분하여 각각의 추정 회귀계수 hat_beta_i를 구함
- 추정해낸 회귀 모델은 아래와 같음.
회귀 계수의 의미
- beta_j는 타 변수가 일정할댸 j번째 변수가 변동시 Y의 변동량
- beta_j = Y에 대한 X_j의 기여도
- beta가 양수이면 X가 증가시 Y도 증가
입력 변수의 중요도
- 선형 회귀 모형에서 변수 중요도는 t value로 측정
- j번째 입력 X_j에 대한 t는 아래와 같이 정의 (SE는 표준 오차)
- SE(hat_beta_j)는 j번째 회귀계수 추정치 hat_beta_i의 표준오차
->t의 절대값이 클수록 영향력이 크다고 할 수 있다.
모형의 적합도 1 - F value
- F value : 모형 상수항 beta_를 제외한 모든 회귀계수가 0인지 아닌지 검정하는 측도
-> F value는 회귀 직선으로 평균적으로 설명가능한 부분(mean squared regression:MSR)을
설명할수없는 부분(mean sqared error; MSE)로 나눈값.
=> 에러에 비해서 직선이 얼마나 설명력이 큰가.
ex. MSE가 매우크다 -> F는 작다 -> p value가 더크다
-> 귀무 가설(모든 회귀 계수가 0)이다 채택 -> 유용하지 않은 회귀직선
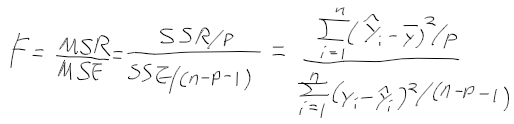
- F value가 크면 입력변수들 중에서 하나는 유의(회귀 계수가 0이 아님).
- F value가 작아서 p value가 크다면 모든 입력가 유의하지 않으므로, 회귀 직선이 유용하지 않음.
모형의 적합도 2 - R-sqaured 결정계수
- 모형의 적합도 goodness of fit를 결정계수 (coefficient of determination) Rsquared로 측정
- 결정계수 R2 : 직선이 설명하는 부분의 총합/ 변동의 총합으로 0~1값
- R squared는 변수 갯수가 많아질수록 증가함
=> adjusted R square 사용
회귀 모형으로 예측
- 새로운 입력 x_1i*, x_2i*, ..., x_pi*을 회귀식에 대입하여 hat_y_i*를 얻음.
예측력
- 회귀 모형이 얼마나 좋은지는 MSE를 주로 사용
로지스틱 회귀모형
- 목표 변수가 0, 1인 경우 아래와 같은 선형 회귀모형으로 설명할수가 없음.
- y_i = 0 또는 1은 힘드니 P(y=1) or P(y = 0)으로 다루자.
- 목표변수가 1이 될 확률을 pi_i = P(y_i = 1)이라 할때 아래와 같이 로지스틱 회귀모형 정의
*성공확률 pi_i는 확률이므로 0~1사이 값
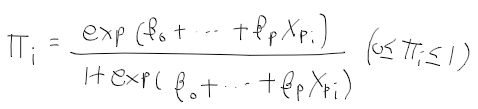
- pi_i의 오즈비는 양수값의 범위를 가짐.
- 로짓의 범위는 실수 영역이 됨. 우리가 구하고자하는 선형 회귀모형이 나옴.
- 성공 확률 pi와 입력변수는 로지스틱 반응함수 형태(S 형태의 곡선으로 나타남)로 표현
- 입력 변수와 로짓의 관계는 직선이 됨.
로지스틱 회귀모형의 모수 추정
- 로지스틱 회귀모형의 모수는 최대가능도 추정법 maximum likelihood estimation method MLE로 추정
- 가능도 함수를 최대화하는 모수 추정값은 뉴턴 랩슨이나 피셔 스코어링 방법으로 구함.
모형을 이용한 예측
- hat pi_i*이 크면 hat_y_i* = 1, 작은경우 hat_y_i* = 0
- pi_0는 0.5를 사용하나 적용 분야에 따라 달리 결정가능.
분류성능 평가지표 Confusion Matrix
- 볼떄마다 맨날 햇갈린다.
- TP True Positive : 실제로 참이고 참으로 판단.
- TN True Negative : 실제로 거짓이고 거짓으로 판단.
- FP False Positive : 실제로 거짓이나 참이라 판단.
- FN False Negative : 실제로 참이나 거짓이라 판단.
- 정밀도 precision = TP/(TP+FP) : Positive 정답률. 모델 예측이 실제로 맞은 비율
- 재현율 recall = TP/(TP+FN) : 민감도라고도 하며, 실제 참 중에서 모델이 참이라고 맞춘 비율
- 정확도 accuracy : 옳게 판단한 비율
Fall-OUT
- FPR(False Positive Rate) = FP/(TN + FP)
- 실제 거짓중에 모델이 True라한 비율
-> 낮을수록 좋음.
TPR(=Recall 재현율)
- TPR = TP/(TP + FN)
- 실제 참중에 모델이 참이라 한 비율
-> 높을 수록 좋음
ROC(Receiver Operating Characterisitc) Curve
- FPR이 작고, 재현률(TPR)이 클수록 좋음
- 곡선이; 왼쪽에 가까울수록 좋은 모델
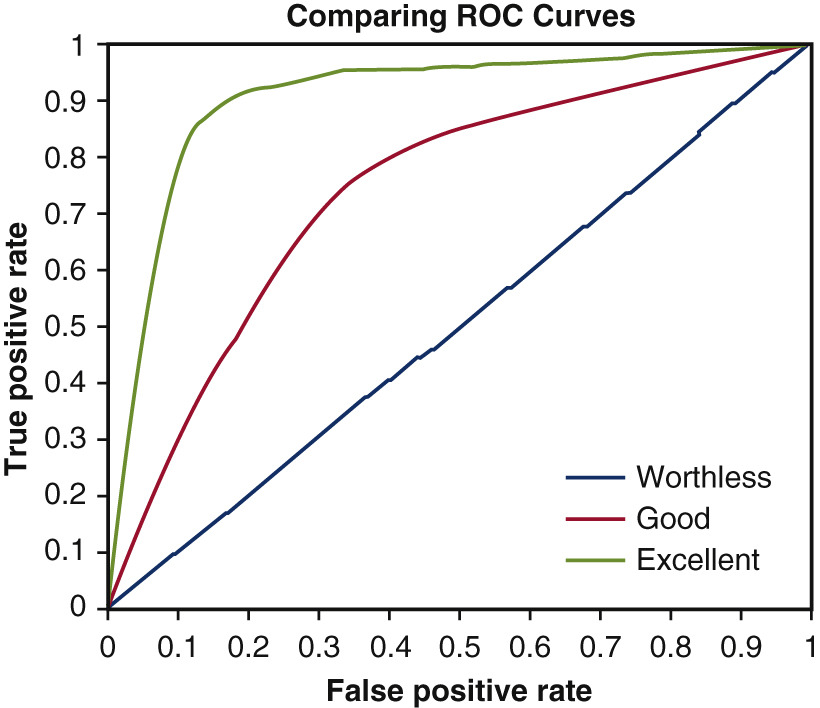https://www.jtcvs.org/article/S0022-5223(18)32875-7/fulltext